(※今回は相当に難解な内容になっちゃったかもしれません)
先日はてブを沢山集めた記事で「平均への回帰」「見せかけの回帰」「共和分」について紹介したんですが、こちらのブログで言及を頂いたようです。
はっきり言って僕が書くよりも大変丁寧な説明をされているようなので僕が何か付け足す必要はなさそうなんですが(笑)、ついでなのでRでどうやって実践するか?というところまで含めて書いてみようと思います。
ちなみに僕がいつも読んでいるテキストが取り上げられていたので、こちらでもご紹介。マルコフ転換モデルの提唱者、James D. Hamiltonのラボに留学されていた沖本竜義先生という、一橋大の先生が書かれた本です*1。

経済・ファイナンスデータの計量時系列分析 (統計ライブラリー)
- 作者: 沖本竜義
- 出版社/メーカー: 朝倉書店
- 発売日: 2010/02/01
- メディア: 単行本
- 購入: 4人 クリック: 101回
- この商品を含むブログ (3件) を見る
はっきり言って、初学者が読むには難解過ぎる本だと思いますが(笑)、計量時系列分析のほぼ全トピックがコンパクトかつ網羅的に紹介されている上に、沖本先生の個人サイトに演習用データが置かれているので、僕個人はバイブルとしていつも脇に置いて参照しています。
ということで、僕自身の復習も兼ねて単位根過程・見せかけの回帰・共和分についてちょっと書いてみます。そうそう、初学者の方がこの記事だけ見て勉強した気になるのは非常に危険ですので、できるだけ上記の沖本先生の本だけは読むようにして下さい。
以下の内容はほぼ全て、上記の沖本先生の本を参考にしたり引用したものです。ご承知置き下さい。
必要なRパッケージ
{forecast}, {tsDyn}, {vars}, {urca}をインストールして展開して下さい。なお{tseries}など依存パッケージとして同時にインストールされるものは、追加インストールは不要です。
前提知識:定常過程、ARIMA、VAR
定常過程
ある時系列の期待値(平均)と自己共分散が常に一定な場合「定常過程」と呼ばれます。要するに「常にだいたい一定の値の周りをばらつく」時系列のことです。大局的に見ると真っ平ら。
ARIMA(自己回帰和分移動平均)過程
ある時系列が、自分自身の過去の値(p時点前まで)の線形和*2と、同様の構造をしたホワイトノイズ*3の(q時点前まで)の線形和*4で表される場合、ARMA(p,q)過程と呼びます。
そしてこの時系列のd階差分をとったARMA系列が定常かつ反転可能*5な時、これをARIMA(p,d,q)過程と呼びます。
これは要するに、ある時系列がどのような内部モデルに従ってばらついているかをモデリングするものです。ここでそれぞれの係数と次数(p,d,q)とを推定すれば、ぶっちゃけ短期的になら未来予測を行うことも可能です。
なお、Rではarima.sim {stats}関数でARIMA(p,d,q)過程をランダムに発生させることができます。またauto.arima {forecast}関数で、探索的方法とAICによるモデル選択によって最適なARIMA過程の次数(p,d,q)を推定することができます。
x.ts<-arima.sim(list(order=c(2,1,1),ar=c(0.2,-0.1),ma=0.1),n=200) # ARIMA(2,1,1)過程を200点発生させる x.arima<-auto.arima(x.ts,trace=T,stepwise=T) # 発生させたx.ts系列のARIMA次数を推定する
VAR
これらの時系列を多変量(すなわち各時点での値がスカラーを並べたもの=ベクトルで表される)に拡張して表現したものをベクトル自己回帰(VAR)過程と呼びます*6。
例えば2変量VAR(1)過程ならこう書けます。
これを多変量のVAR(p)過程に拡張するとこう書けます。
(ただしは
定数ベクトル、
は
係数行列)
RではVAR.sim {tsDyn}関数でVAR(p)過程をランダムに発生させることができます。またVARselect {vars}関数で次数を推定し、VAR {vars}関数で係数を推定することで、VAR(p)過程を推定することができます。
B1<-matrix(c(0.7, 0.2, 0.2, 0.7), 2) x<-VAR.sim(B=B1,n=100,include="const") x.p<-VARselect(x.var,lag.max=10,include="const")$selection[1] x.var<-VAR(x,p=x.p,type="const")
VARモデルにすることで、今度は多変量の場合の内部モデルを推定することができ、多変量のそれぞれについて未来予測を行うこともできる、というわけです。
単位根過程
ARIMA過程のうち、特に元の時系列が非定常過程である一方で差分系列
が定常過程である時、これを単位根過程(もしくは和分過程)と呼びます。
もっとも分かりやすい例はランダムウォークでしょう。その数理モデル(幾何ブラウン運動)についてはWikipedia記事が分かりやすいと思います。Rではシンプルに乱数の累積値を取ることでシミュレーションできます。以前も引用させて頂いたteramonagiさんのブログ記事で例示されている通り、例えば
# Term(year) T <- 5 # Number of path N <- 10000 # Unit of time dt <- T / N # Start price of stock or something obeying to geometric brownian motion s0 <- 100 # montecarlo simulation(Average return 10%(per annual), Volatility 20%(per annual)) x <- s0 * exp(cumsum(0.1 * dt + 0.2 * rnorm(N) * sqrt(dt))) y <- s0 * exp(cumsum(0.1 * dt + 0.2 * rnorm(N) * sqrt(dt))) # plot matplot(cbind(x,y))
のようにすることで、2つのランダムウォークを発生させることができます。
ちなみにARIMA(p,1,q)過程は単位根過程のひとつとして見ることもできます。もちろんarima.sim {stats}関数でランダムに発生させることが可能です。
sr_x<-arima.sim(list(order=c(2,1,1),ar=c(0.2,-0.1),ma=-0.1),n=200) # ARIMA(2,1,1)過程 sr_y<-arima.sim(list(order=c(0,1,1),ma=0.2),n=200) # ARIMA(0,1,1)過程
一般に単位根過程はトレンド過程(つまり上か下にずーっと増えたり減ったりしていく)のことも表します。多くの経済・ファイナンスデータのように「前の時点の値に今の時点でのランダムな値が足し算されていく」ような時系列は、大体において単位根過程と言って良いと思います。
見せかけの回帰
さぁ、いよいよ本題です。ここからが超難物。
まず先にRでシミュレートしてみるのが最も手っ取り早いでしょう。上記のarima.sim関数で発生させたARIMA(2,1,1)過程sr_xと、ARIMA(0,1,1)過程sr_yについて、試しにsr_yをsr_xで回帰してみます。すると、シミュレーションの結果次第ですが
> summary(lm(sr_y~sr_x)) Call: lm(formula = sr_y ~ sr_x) Residuals: Min 1Q Median 3Q Max -14.148 -2.706 1.185 3.220 8.604 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 12.56891 0.82481 15.24 <2e-16 *** sr_x 0.64303 0.03574 17.99 <2e-16 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 5.004 on 199 degrees of freedom Multiple R-squared: 0.6192, Adjusted R-squared: 0.6173 F-statistic: 323.6 on 1 and 199 DF, p-value: < 2.2e-16
ハァ? 完全に乱数に従って発生させたはずの2変数なのに、R二乗値が0.6192??? p値に至ってはp < 2.2e-16??? これをプロットしてみるとこうなります。
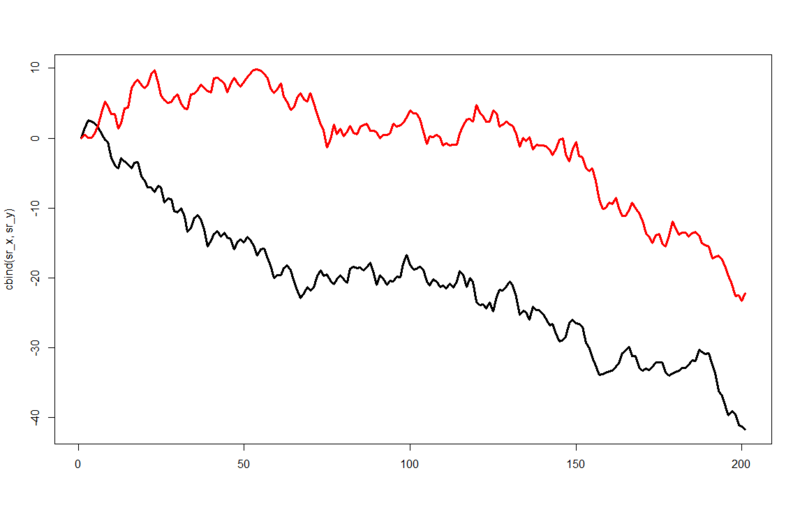
これはさすがに回帰関係が生じても仕方ないかなー、という気はします。ただ、これではあまりにも信じ難いのでもう一例やってみましょう。今度はARMA係数を少しいじって。。。
> sr_x<-arima.sim(list(order=c(2,1,1),ar=c(0.2,0.3),ma=-0.1),n=200) > sr_y<-arima.sim(list(order=c(0,1,1),ma=0.2),n=200) > summary(lm(sr_y~sr_x)) Call: lm(formula = sr_y ~ sr_x) Residuals: Min 1Q Median 3Q Max -8.1869 -3.1409 0.4504 3.0100 7.4765 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 6.89268 0.45756 15.064 < 2e-16 *** sr_x -0.10603 0.03219 -3.294 0.00117 ** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 3.911 on 199 degrees of freedom Multiple R-squared: 0.0517, Adjusted R-squared: 0.04693 F-statistic: 10.85 on 1 and 199 DF, p-value: 0.00117 > matplot(cbind(sr_x,sr_y),type="l",lwd=3,lty=1)

パッと見では回帰関係なんかなさそうに見えるのに、やっぱり有意な回帰が出てます。何回見てもこれは不思議ですよねー。
ところで、何故見せかけの回帰は起きるんでしょうか? 原理的な側面について、以下沖本先生の著書pp.126-127より引用します。
見せかけの回帰の現象を定義するために、2つの独立なランダムウォークを考えよう。具体的には、
と
を独立なiid系列として、
と
を
で定義する。このとき、
と
は独立なランダムウォークであるので、
(6.3)
となる回帰モデルを考えたとすると、真の値は
となる。したがって、(6.3)をOLSで推定し、
という仮説検定を行うと、
が採択される確率が高いはずである。しかしながら、変数の非定常性が驚くべき結果をもたらすことが知られている。具体的には、(6.3)をOLDで推定したときのOLS推定量
と
について、
(6.4)
が成立することが知られている*7。ここで
と
を独立な標準ブラウン運動として、
である。(6.4)の結果は、
が
の速度で発散し、
がある確率変数に収束することを示している。これは、
の速度で真の値に収束していく標準的な場合や、
の速度で真の値に収束していく単位根検定統計量の場合とは非常に異なるものであり、
も
も一致推定量ではないことがわかる。また、このため、
と
に関するt統計量は発散することになる。つまり、
が大きいとき、
と
を用いてt検定を行うと、ほぼ確実に
と
という帰無仮説は棄却されるのである*8。また、もう1つの驚くべき事実として、回帰の決定係数
が漸近的に1に収束することも知られている。
もう少し説明を補足すると、要はと
が異なるスピードで真の値に収束しようとしてしまうので、この2つの推定に関連するt統計量が勝手に発散(爆発的に増大)してしまう、ということです。言うまでもなく通常の回帰分析、OLSはt統計量の大小で有意か否かを判定しますので、結果的に「大体いつも有意」ということになってしまうというわけです。
この現象は最初にGrangerとNewboldが当時始まったばかりのモンテカルロシミュレーションによって発見し(Granger & Newbold, 1974)、その後Phillipsが解析的な証明を与えたものです(Phillips, 1986)。興味のある方はぜひPhillipsの論文もお読みください。僕は読み通せませんでしたが。笑
ともあれ、このように見せかけの回帰が生じている状況でVARモデルを推定しても、結果はぐちゃぐちゃに歪んでしまいます。そのため、まずはVARモデルに含まれる全ての時系列に対して単位根検定を実施する必要があります。これはadf.test {tseries}関数で実施できます。
> adf.test(sr_x) Augmented Dickey-Fuller Test data: sr_x Dickey-Fuller = -1.8622, Lag order = 5, p-value = 0.6338 alternative hypothesis: stationary > adf.test(sr_y) Augmented Dickey-Fuller Test data: sr_y Dickey-Fuller = -2.079, Lag order = 5, p-value = 0.543 alternative hypothesis: stationary
対立仮説は「定常」(つまり単位根「ではない」)でこれが棄却されたので、sr_x & sr_yとも単位根過程であるということが分かります。このような場合は、全ての時系列から1階差分を取ってVARモデルを計算する必要があります。
共和分
ところが、中には単位根過程同士であっても何故か見せかけの回帰が起きないケースがあります。以下のソースをご覧頂きたいのですが、
> adf.test(x_ci) Augmented Dickey-Fuller Test data: x_ci Dickey-Fuller = -1.488, Lag order = 5, p-value = 0.7905 alternative hypothesis: stationary > adf.test(y_ci) Augmented Dickey-Fuller Test data: y_ci Dickey-Fuller = -1.3165, Lag order = 5, p-value = 0.8624 alternative hypothesis: stationary > summary(lm(y_ci~x_ci)) Call: lm(formula = y_ci ~ x_ci) Residuals: Min 1Q Median 3Q Max -9.548 -6.178 -3.125 6.718 13.851 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -12.2700 0.9531 -12.874 <2e-16 *** x_ci -0.2409 0.1904 -1.265 0.207 --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 7.393 on 199 degrees of freedom Multiple R-squared: 0.007983, Adjusted R-squared: 0.002998 F-statistic: 1.601 on 1 and 199 DF, p-value: 0.2072 > matplot(cbind(x_ci,y_ci),lwd=3,lty=1,type="l")

ごらんの通り、このケースではp = 0.2ぐらいということで見せかけの回帰が起きていません。これは、たまたま上記の例と同じように適当にARIMA(2,1,1)過程とARIMA(1,1,1)過程を発生させていたら出てきた事例です。このような状態にある時、これらの時系列は「共和分」の関係にあると呼びます。具体的な定義は沖本先生の本のp.129より引用。
と
を単位根(
)過程とする。
が定常(
)過程となるようなaとbが存在するとき、
と
との間には共和分(cointegration)の関係がある、もしくは
と
は共和分している(cointegrated)といわれる。より一般的には、
を
とする。
が
過程となるような
が存在するとき、
には共和分の関係がある、もしくは
は共和分しているといわれる。また、このとき、
や
は共和分ベクトル(cointegrating vector)を呼ばれる。
これは端的に言うと、長期的にはなる傾向が生じるということで、2つの変数間には均衡関係がある=2つの変数の(線形)和が一定、ということを示しています。つまり、単位根=和分過程だらけの経済・ファイナンスによくある時系列の中にあって、もし均衡関係を持っているものがあればこの共和分のモデルで説明できる!ということも意味しているというわけです。
ところで、単位根過程を含むVARモデルは仮に共和分関係を含んでいて変数間で見せかけの回帰が生じなかったとしても、そのままでは正しく推定できません(見せかけの回帰を生じさせる変数の組み合わせがあればなおさら)。なので、共和分関係を修正したモデルを新たに推定し、これをVARモデルに変換(解釈といった方が妥当かも)する必要があります。それがベクトル誤差修正モデル(VECM: vector error correction model)です。沖本先生の本では、共和分ベクトルを推定して誤差修正項を与える方法論として、Johansenの方法(Johansen, 1991)*9が紹介されています。
VECMの定義は複雑なのでここでは紹介しません。代わりに、RでVECM及びVARへの変換モデルを推定する方法について紹介しておきます。必要なのは{urca}と{vars}です。ちなみに良いサンプルデータを自前で作ることができなかった*10ので、これだけ{urca}のサンプルを借用します。ごめんなさい。
利用するのはJohansenが参照したというデータセット"finland"です。まずは単位根検定をかけてみます。
> attach(finland) > adf.test(lrm1) Augmented Dickey-Fuller Test data: lrm1 Dickey-Fuller = -2.5459, Lag order = 4, p-value = 0.3503 alternative hypothesis: stationary > adf.test(lny) Augmented Dickey-Fuller Test data: lny Dickey-Fuller = -1.5649, Lag order = 4, p-value = 0.7571 alternative hypothesis: stationary > adf.test(lnmr) Augmented Dickey-Fuller Test data: lnmr Dickey-Fuller = -3.8297, Lag order = 4, p-value = 0.02011 alternative hypothesis: stationary > adf.test(difp) Augmented Dickey-Fuller Test data: difp Dickey-Fuller = -2.5159, Lag order = 4, p-value = 0.3627 alternative hypothesis: stationary
4変数中、3つが単位根過程だということが分かりました。そこで、これを表現するVECMモデルを推定するために、ca.jo {urca}関数を使います。この関数の返値はVECMの各パラメータを含んでいます。また共和分ランクを10%, 5%, 1%棄却域に分けて検定した結果も含まれていて、summary関数でチェックすることができます。
> data(finland) > sjf<-finland > sjf.vecm<-ca.jo(sjf,ecdet="none",type="eigen",K=2,spec="longrun",season=4) > summary(sjf.vecm) ###################### # Johansen-Procedure # ###################### Test type: maximal eigenvalue statistic (lambda max) , with linear trend Eigenvalues (lambda): [1] 0.30932660 0.22599561 0.07308056 0.02946699 Values of teststatistic and critical values of test: test 10pct 5pct 1pct r <= 3 | 3.11 6.50 8.18 11.65 r <= 2 | 7.89 12.91 14.90 19.19 r <= 1 | 26.64 18.90 21.07 25.75 r = 0 | 38.49 24.78 27.14 32.14 Eigenvectors, normalised to first column: (These are the cointegration relations) lrm1.l2 lny.l2 lnmr.l2 difp.l2 lrm1.l2 1.0000000 1.000000 1.0000000 1.000000 lny.l2 -0.9763252 -1.323191 -0.9199865 1.608739 lnmr.l2 -7.0910749 -2.016033 0.2691516 -1.375342 difp.l2 -7.0191097 22.740851 -1.8223931 -15.686927 Weights W: (This is the loading matrix) lrm1.l2 lny.l2 lnmr.l2 difp.l2 lrm1.d 0.033342108 -0.020280528 -0.129947614 -0.002561906 lny.d 0.022544782 -0.005717446 0.012949130 -0.006265406 lnmr.d 0.053505000 0.046876449 -0.007367715 0.002173242 difp.d 0.005554849 -0.017353903 0.014561151 0.001531004
ということで、このデータには共和分ランクr = 2が認められます*11。これをVAR表現に直すにはvec2var {vars}関数を用いて以下のようにします。
> sjf.vec2var<-vec2var(sjf.vecm,r=2) > print(sjf.vec2var) Coefficient matrix of lagged endogenous variables: A1: lrm1.l1 lny.l1 lnmr.l1 difp.l1 lrm1 0.855185363 -0.28226832 -0.09298924 -0.1750511 lny 0.036993826 0.33057494 -0.06731145 -0.1946863 lnmr -0.156875074 -0.01067717 0.76861874 0.4247362 difp 0.001331951 0.02850137 0.02361709 0.2063468 A2: lrm1.l2 lny.l2 lnmr.l2 difp.l2 lrm1 0.15787622 0.27655060 -0.10255593 -0.52017728 lny -0.02016649 0.65497929 -0.08102873 -0.09357761 lnmr 0.25725652 -0.10358761 -0.24253117 0.26571672 difp -0.01313100 -0.01096218 -0.02802090 0.36002057 Coefficient matrix of deterministic regressor(s). constant sd1 sd2 sd3 lrm1 0.03454360 0.039660747 0.037177941 0.10095683 lny 0.05021877 0.043686282 0.082751819 0.09559270 lnmr 0.22729778 0.008791390 0.012456612 0.02011396 difp -0.03055891 0.001723883 -0.007525805 -0.00835411
ちなみにこれらの計算で得られたVAR / VECMモデルは、{vars}{urca}双方のパッケージに同梱されているplot関数で図示できますし、predict関数を使えば未来予測を行うこともできます。これで例えばwebデータマイニングの世界で言えば着地予想を計算することも可能です。
今回は、その辺の予測などの話題はVARモデルがメインではなく見せかけの回帰がメインということで、割愛します。機会があればまたRを使ってやりたいところです。
最後に僕個人が勝手に想像している「見せかけの回帰が起きる理由」について
そもそも、何で共和分関係にない2つの単位根過程同士で見せかけの回帰が起きるんだろう?と思って純粋に直感的な説明を考えてみました。
端的に言えば、ランダムウォーク含めて単位根過程はその定義上「一定期間増加or減少」という挙動を繰り返します。その挙動がお互いに重なるタイミングが少しでもあれば、そこに回帰関係が生じる。そしてそのタイミングの多寡で回帰係数の大小と有意度の高低はつくものの、最終的に見せかけの回帰が生じる・・・というのが僕の直感的な理解です。
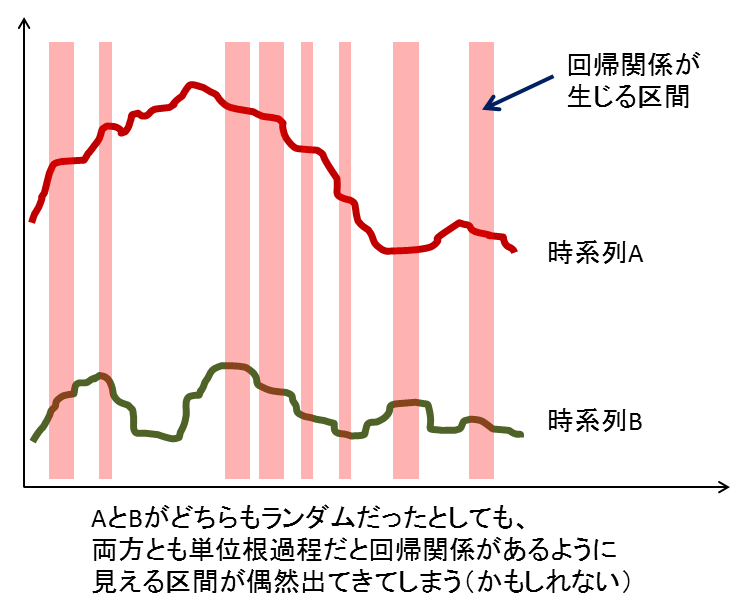
これが共和分関係(双方とも単位根だが両者の和が定常過程に従う=平均が一定値かつランダムにばらつく)だと、回帰をかけても互いにランダムな挙動を示すので、回帰関係は検出されない。つまり見せかけの回帰は生じない・・・のかもしれません。
これはあくまでも僕の勝手な直感的な説明なので、Phillipsの1986年の論文の解釈とは全く異なるかもしれません・・・どなたか教えてください!*12
おまけ1
一応僕も、Hamiltonの大著"Time Series Analysis"の原著を持ってます。

- 作者: James D. Hamilton
- 出版社/メーカー: Princeton Univ Pr
- 発売日: 1994/01/11
- メディア: ハードカバー
- 購入: 1人 クリック: 5回
- この商品を含むブログ (6件) を見る
なのですが、共和分のところ以外は(沖本先生の本があるのも手伝って)真面目に読んでません。笑 前の部署の部下だったスイス人のR君に輪読をやってもらってたんですが、2人とも異動してしまったので以後輪読は進まず・・・誰か一緒に輪読やりませんか?笑
おまけ2
なお、一連の計量時系列分析について、非常に端的かつ簡潔なまとめがこちらのページにあります。
*1:既にAmazonでは品切れになっているHamiltonの"Time Series Analysis"の邦訳版の訳者でもおられる
*2:これがAR(自己回帰)過程
*3:平均が0、分散が一定で自己相関が0のランダムな時系列。正規分布に従うと仮定するケースが多い
*5:ARMA過程の反転可能性はMA過程部分のMA特性方程式のすべての解の絶対値が1より大きい時に成り立つ。MA特性方程式についてはここでは触れない
*6:もちろんVARMA, VARIMAも表現可能だが、あまりにも次数が多過ぎて複雑&計算量が爆発してしまうのとVARで十分にモデリングできるため、一般にはVARが多く用いられる
*7:OLS推定量の表し方の問題なので、別に調べることをお薦めします
*8:t統計量が発散(爆発的増大)してしまい、勝手に回帰関係が統計的に有意という判定になってしまうため
*9:何とデンマーク語で書かれた論文なので、僕は読みたくても読めません。。。
*10:会社のデータにはあるんですが勿論こんなところでは出せません笑
*11:r <= 1が棄却されてr <= 2が採択されているため。右から2番目の5pt点が基準
*12:さすがにあの論文をその疑問が分かるまで読み解く気にはなれないし、ブログで論文輪読とかもう二度とやりたくないので