僕の得意分野は計量時系列分析(Econometric time series analysis)なんですが、実際にソーシャルwebサービス企業でデータ分析に取り組む上ではそんなに細かいことやる必要はない、というかそこまで正確な分析をする前に実務上色々やるべきことがある、ということは結構多いです。
実際のところ、本当は異常値検出・外れ値検出みたいな手法でゴリゴリやりたい(例えばyokkunsさんが提供なさっているRの{ChangeAnomalyDetection}パッケージとか、はたまた{tsDyn}パッケージでも実装されているようなSETARとか、もしくは{MSwM}パッケージでやれるマルコフ状態転換モデルとか)んですが、Rを使ってもらうだけでも一苦労という現場ではそうも言ってられないという実態もあります。
ということで、もう何もかも面倒なのでお手軽に「KPIの上がり下がりを見て『これ凄くね?』『これヤバいんじゃね?』とすぐ言える」ようにするExcelベースのプロットの仕方を適当に紹介します。データサイエンスというよりはアナリティクスの領域かもですが。
Excelでも簡単に求まる「平均」と「標準偏差」で何とかする
とりあえずGitHubにExcelファイルのサンプルを上げておきました。
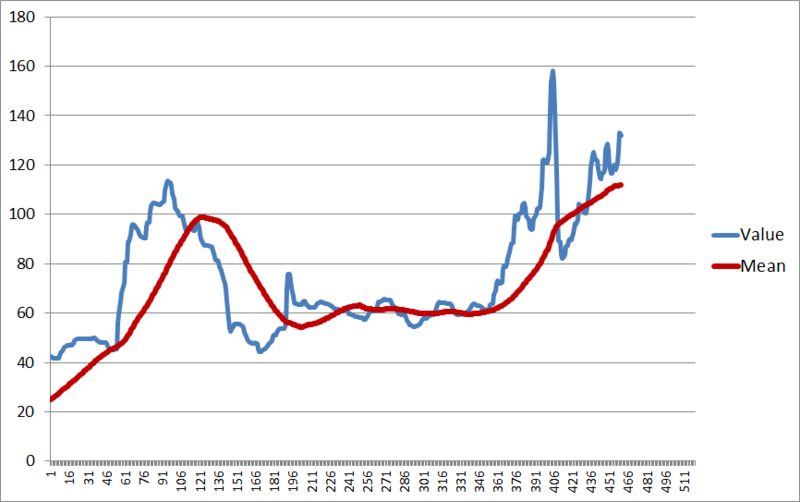
元データは、適当に政府統計局の何がしかを拾ってきたものです。全部で500点ぐらい(確か月次データ)のもの。プロットするとこうなります。

結構ギザギザしてる上に、ところどころズーンと不連続な変化をしているところが見えます。これをできればその瞬間に捕まえたいところ。
そこで、移動平均を計算します。ここでは60点移動平均にしたいので、例えばデータがA列にあるとして
B60 = AVERAGE(A1:A60)
みたいにして、後は最後までオートフィルで並べます。これで60点移動平均したデータが下までズラッと並びます。
次に、標準偏差(慣例的にσ:シグマと呼ばれる)を計算します。同じように60点にまたがって標準偏差を計算したいので、先ほどの例にならえば
C60 = STDEV(A1:A60)
みたいにして、同じように最後までオートフィルで並べます。これでA列に元データ、B列に移動平均、C列に標準偏差があることになります。
±2σで境界線を作り、そこを超えた時のみアラートを出す
そこで、例えばこんな感じにします。
D60 = B60 - 2*C60 E60 = B60 + 2*C60
これをオートフィルしてやると、D列に「移動平均 - 標準偏差の2倍」、E列に「移動平均 + 標準偏差の2倍」が入ることになります。これは何を意味しているかというと、ざっくり言えば「統計的にただの偶然とは言い切れない変動幅」を表します。
ものすごーーーく大ざっぱに書くと、正規分布と±2σ境界線との間には下の図のような関係があります。
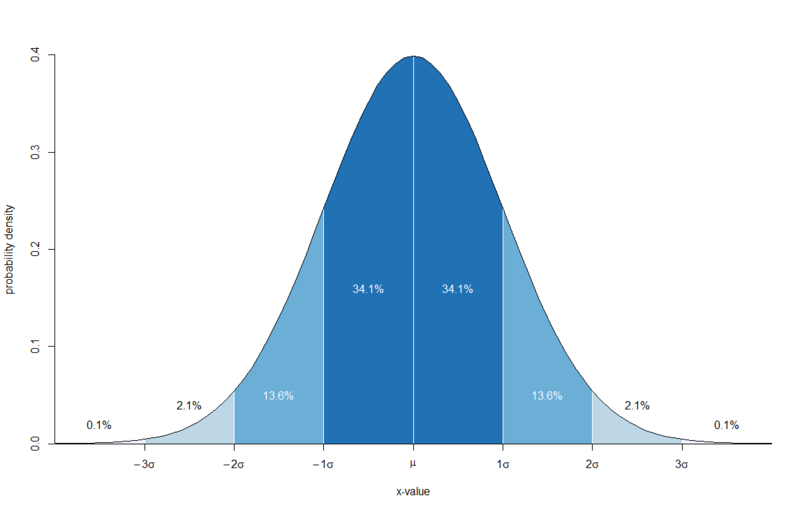
要は「バラツキのうち95%ぐらいまでが±2σの範囲で説明できてこれを偶然の産物とみなす」というわけです。統計学の慣習の一つにこの「95%の範囲を超えたらただの偶然ではなく必然である可能性が高い」というのがあり、それにならおうというわけです。
なお、この図はここにあるコードをそのまま貼り付ければRで描けます。
さて、元の時系列のデータに戻りましょう。まずA列とB列を並べてプロットするとこんな感じになります。
次に、D列とE列を追加します。
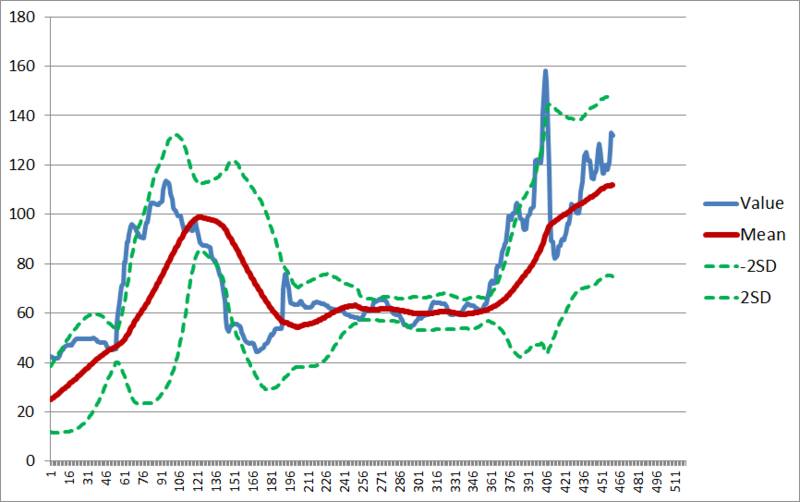
これで±2σ境界線つきの、データプロットが出来上がりました。そこでこの境界線から上下に値が外れているところを明示してみると、

こんな感じで検出されるのが分かります。リアルタイムでもある程度この辺の検出はできるので*1、毎日このプロットを作っておくことでそれなりに異常値に気付きやすくなると思います。
注意点
今回は適当に60点移動平均にしましたが、これが例えば日次データで1週間ごとに周期性*2を見せるようなら、「7日間移動平均」にするとか、はたまた「28日間(4週間)移動平均」にするとか工夫することで、うまく周期性をフィルタリングできます。
ところで、それっぽく書いちゃいましたがこの方法論は統計学的な妥当性という点で言うと果てしなく微妙な代物です。本来なら、最初にも書いたように計量時系列分析などでカッチリやるべきものなので、あまり頼り過ぎてもいけません。あくまでもヘルスチェック目的でどうぞ。
(※厳密な話をしたい人のために付記しておくと、KPIは正規分布しない上に大抵は単変量なら和分を伴うARIMA過程、多変量なら共和分を伴うVAR過程なので、静的データに対する統計学を用いること自体が不適切です。計量時系列分析の諸手法で臨むのが本義だと考えています。個人的にはマルコフ状態転換モデルを推したいところ)
(※※ちなみに今回ここまで強く「グローバルトレンドを重視する」ことを打ち出した背景として、「平均への回帰or見せかけの回帰にハマること」へのアンチテーゼというのを意識しています。よりマシ論とまでは言わないにせよ、少しでも「毎日頑張ってる割にうまくいかない」シチュエーションからの脱却に貢献する方法を模索してみた中での、一つの帰結ということで)
(※※id:aaaazzzz036さんから言及を頂きました→「平均値0, 分散1にした対称な連続分布いろいろ」)