追記
2016年3月に以下の記事によってこの内容はupdateされています。今後はそちらをお読み下さい。
主に自分向けのまとめという意味合いが強いんですが(笑)、僕が実際に2013年6月現在webデータ分析&データサイエンスの実務でツール・ライブラリ・パッケージを利用しているものに限って、統計学・機械学習系の分析手法を10個挙げて紹介してみようと思います。
- 追記
- 回帰分析(特に線形重回帰分析)
- 独立性の検定(カイ二乗検定・フィッシャーの正確確率検定)
- 主成分分析(PCA) / 因子分析
- クラスタリング
- 決定木 / 回帰木
- サポートベクターマシン(SVM)
- ロジスティック回帰
- ランダムフォレスト
- アソシエーション分析(バスケット分析・相関ルール抽出)
- 計量時系列分析
- おわりに
基本的にはどれも僕が戦略マーケティング部門で実務として行っているアドホック分析向けの手法で、
- 僕自身が知っていても実務ではほとんど使っていないもの
- レコメンドなどバックエンドシステム向けの手法
- 機械学習の諸手法のバックエンドシステム向けの実装方法
- Deep learningとか巷では有名でも個人的にはまだ実務で使ったことのないもの
- ベイジアンなどそもそも僕が不得手なもの
などは外してあります。悪しからずご了承を。なお、僕の仕事内容が変わる度に今後このシリーズはアップデートされていく・・・予定です、たぶん(笑)。
ちなみに、今回も統計学的・機械学習的な厳密性はある程度度外視して、ものすごく大ざっぱな説明に留めるつもりです。細かいポイントはまた改めて、ということで。そして、どれもR / SPSSなら大体使えるものばかりです。初めてRを使うという人は、以前の記事(素性ベクトル+分類ラベルのテーブルを持ってくる⇒Rを使ってお手軽に機械学習で分類してみる)などを参考に、実行環境を準備した上でトライしてみて下さい。
(※基本的に「どんな手法を使っているか」「どういうツール・ライブラリ・パッケージを利用すればその手法が使えるか」にのみフォーカスした記事なので、厳密性にかかわる部分は全て度外視しています。悪しからず)
回帰分析(特に線形重回帰分析)
猛烈に大ざっぱに書くと、
売上高 = a * ヘビーユーザーDAU + b * ライトユーザーDAU + c * 呼び戻しユーザーDAU
のように仮に数値モデルを立てて、実データから逆算してそれぞれの係数a, b, cを推定することでモデルの全体像を求める手法のことです。主にDAUとか売上高とか「何かと何かを足し合わせたりかけ合わせることで得られるであろう数値」のモデル化に向いています。
Rではこんな感じで実践できます。サンプルデータとしてはairqualityを使ってます。ちなみにプロットするとこんな感じのデータで*1、黒いプロットで表されるオゾン濃度を説明するモデルを探す感じです。

> data(airquality) # データ読み込み > airq<-airquality[,1:4] # 月・日付のデータを外す > airq.lm<-lm(Ozone~.,airq) # Ozone = a * Solar.R + b * Wind + c * Temp + dのモデルを推定する > summary(airq.lm) # 結果を表示する Call: lm(formula = Ozone ~ ., data = airq) Residuals: Min 1Q Median 3Q Max -40.485 -14.219 -3.551 10.097 95.619 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -64.34208 23.05472 -2.791 0.00623 ** Solar.R 0.05982 0.02319 2.580 0.01124 * Wind -3.33359 0.65441 -5.094 1.52e-06 *** Temp 1.65209 0.25353 6.516 2.42e-09 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 21.18 on 107 degrees of freedom (42 observations deleted due to missingness) Multiple R-squared: 0.6059, Adjusted R-squared: 0.5948 F-statistic: 54.83 on 3 and 107 DF, p-value: < 2.2e-16 > airq.lm<-lm(Ozone~. - 1,airq) # 切片dを除外する > summary(airq.lm) Call: lm(formula = Ozone ~ . - 1, data = airq) Residuals: Min 1Q Median 3Q Max -40.675 -15.446 -5.526 13.479 88.822 Coefficients: Estimate Std. Error t value Pr(>|t|) Solar.R 0.06306 0.02387 2.641 0.00948 ** Wind -4.59884 0.48653 -9.452 8.21e-16 *** Temp 0.98525 0.08739 11.275 < 2e-16 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 21.84 on 108 degrees of freedom (42 observations deleted due to missingness) Multiple R-squared: 0.8383, Adjusted R-squared: 0.8338 F-statistic: 186.7 on 3 and 108 DF, p-value: < 2.2e-16
オゾン濃度には気温がプラスの影響を、風速がマイナスの影響を与えていることが分かりますね。ちなみに交互作用とかモデル選択の問題*2とか細かい点は、ややこしくなるのでここでは割愛。また今回はやりませんでしたが、predict()関数でモデルに基づいた予測を行うこともできます。
なお、Rを使う人はこの回帰分析のところで出てくる
y ~ x1 + x2 + x3 + ... # 回帰モデル y ~ . # 回帰モデル(全部入り)
のようなformula記法に慣れておくと良いと思います。回帰モデル及びformula記法はその他の重要な線形検定モデル(例えば分散分析など)でも使うことになるので、覚えておいて損はないです。
独立性の検定(カイ二乗検定・フィッシャーの正確確率検定)
何か施策を打った際のKPIに対する効果検証を行う際には必須です。特にA/Bテストで改善施策がコンバージョンUU数を増やしたかどうか調べたい!という時には、CVRだけ見ていても往々にして分母が違っていてそのままでは比較できないケースが多いので、この方法論を知っていることは重要です。
(以前のブログ記事も参照のこと:「カイゼンしたらコンバージョン率が○○%→△△%にup!」は分母を無視したら成り立たないかもしれない)
Rではchisq.test()関数やfisher.test()関数で実践できます。サンプルとして、昔からよく知られている「予防注射の効果の有無」のデータを用意してみました。
| 病気にかからない | かかった | |
|---|---|---|
| 注射した | 1625 | 5 |
| 注射しない | 1022 | 11 |
> x<-matrix(c(1625,5,1022,11),ncol=2,byrow=T) # データをマトリクスとして与える > print(x) # 確認 [,1] [,2] [1,] 1625 5 [2,] 1022 11 > chisq.test(x) # カイ二乗検定 Pearson's Chi-squared test with Yates' continuity correction data: x X-squared = 4.8817, df = 1, p-value = 0.02714 # 有意:予防注射には効果がある > fisher.test(x) # フィッシャーの正確確率検定 Fisher's Exact Test for Count Data data: x p-value = 0.01885 # 有意:予防注射には効果がある alternative hypothesis: true odds ratio is not equal to 1 95 percent confidence interval: 1.115982 12.879160 sample estimates: odds ratio 3.496373
「予防注射には効果があった」という結論になっています。同じように微妙なケースって結構A/Bテストでは多いと思うので、知っておいて損はないでしょう。
主成分分析(PCA) / 因子分析
データがごちゃごちゃしていて、ある程度どういう方向性にデータが割れているか絞り込みたい!という時に使える手法です。この2つ、良くそっくりだと言われるんですが大まかに言えば
- モデルなしで、多くの変数を少ない変数に集約するのが主成分分析
- モデルありで、多くの変数を共通因子にまとめるのが因子分析
といった違いがあります。ともあれ、全体の傾向としてデータがどの方向性に向かって分布しているかを知りたい時にはどちらの手法も非常に有用です。
主成分分析の例として、Rにデフォルトで入っているサンプルデータUSArrestsを用いてみます。物騒な変数名が並んでますが、これは1973年の全米50州での主要な犯罪によって逮捕された容疑者の数を10万人ごとの数字にして表したものです。
> data(USArrests) > pc.cr<-princomp(USArrests,cor=T) # princomp()が主成分分析を行う関数 > biplot(pc.cr)
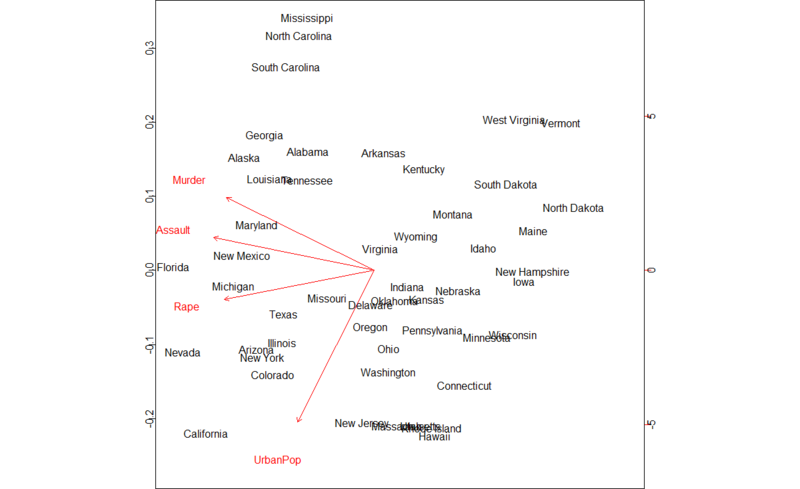
物騒な州はどの辺か?がこのプロットから分かってしまいますね*3。。。
一方、因子分析の例としてはこちらのページのサンプルを拝借することにします。ある学校で学生に「どの教科が好きor嫌い?」を5段階で答えてもらったデータだそうです。
> data <- read.csv("dataset_exploratoryFactorAnalysis.csv") > data.fac<-factanal(data,factors=3,scores="regression") # factanal()関数で因子分析。因子数を3に設定 > biplot(data.fac$scores,data.fac$loadings)
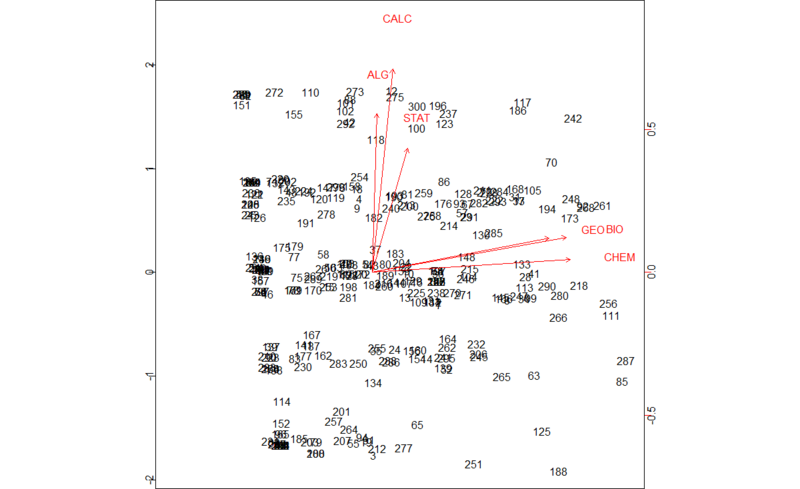
教科の好き嫌いが2系統に偏っていることが見て取れますね。ちなみに、同じデータに対して主成分分析を行ってもほぼ同様の結果になります。
クラスタリング
大ざっぱに言えば、「データの組み合わせが似たもの同士をまとめる」分析方法です。イメージとしては、「ゲームAとゲームBをやっている人たち」vs.「ゲームCとゲームDをやっている人たち」のように、利用しているサービスの組み合わせごとにグルーピングできるんじゃないか?というケースで、それを実際にUUベースで切り分ける方法論と言って良いでしょう。
データが小さければ、階層的クラスタリングという手法が使えます。上の「どの教科が好きor嫌い」データをそのまま使うと、こんな感じになります。
> data <- read.csv("dataset_exploratoryFactorAnalysis.csv") > data.d<-dist(data) # 個々のデータ間のユークリッド距離を求める > data.cls<-hclust(data.d) # hclust()が階層的クラスタリングの関数 > plot(data.cls)
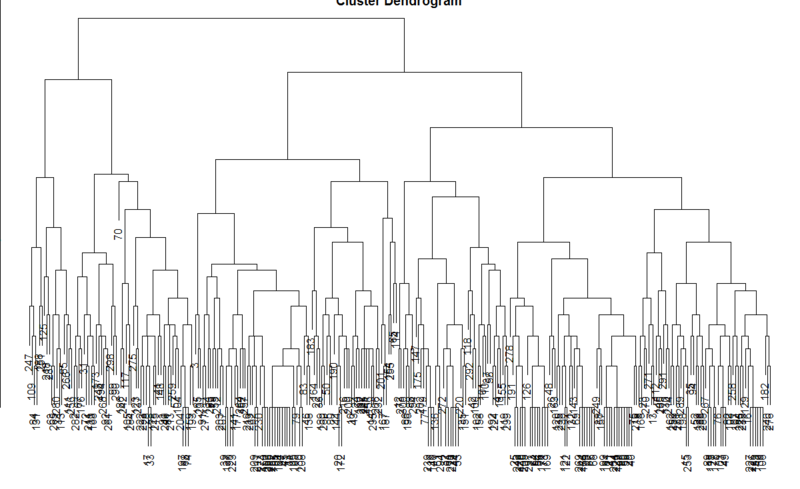
すいません、図のタイトルがはみ出しました(笑)。こんな感じのデンドログラム(樹状図)でどの教科が好きor嫌い?ごとにグループが分かれていくのが見て取れます。
なお、データサイズが大きい時はhclust()関数ではさばけないことが多いので、k平均クラスタリングを行うkmeans()関数を使った方が無難です。ただしデンドログラムを表示することは基本的にはできず、個々のデータにどのクラスタに割り振られたかを示すインデックスだけがつく、という感じです。
決定木 / 回帰木
実際にUUベースでのwebデータ分析では、これが一番人気があると思います。要するに、例えば「翌月定着or離脱した」と言った分類ラベル+「どの行動を当該期間内にとったか」と言った素性ベクトルに基づいて「何が定着or離脱とを分けたか(ガチャを引いた、他ユーザーとつながったetc.)」を樹状図の形で表す手法です*4。
これはデータの表示方法が直感的で分かりやすいため、多くのwebデータ分析の現場で使われています。中には全自動化して自前でパッケージ化して誰でもアクセスできるようにしているところもあるようです。
Rでは以下のような感じでできます。これまたあまり楽しくないデータですが、Rにデフォルトで入っている「タイタニック号乗客乗員の生存vs.死亡状況を様々なデータとともに分類した」データを用いています。ここでは{mvpart}パッケージを使用します。
> data(Titanic) > z <- data.frame(Titanic) > Titanic1 <- data.frame(Class = rep(z[, 1], z[, 5]), Sex = rep(z[, 2], z[, 5]), + Age = rep(z[, 3], z[, 5]), Survived = rep(z[, 4], z[, 5])) > Titanic1.rp<-rpart(Survived~.,Titanic1) > plot(Titanic1.rp,uniform=T,margin=0.12) > text(Titanic1.rp,uniform=T,use.n=T,all=F)

計算の便宜上カテゴリ分けがa, b, cとなってしまっているので、それぞれが何に対応しているかは生データを見る必要があります。なお、このデータからは「女性もしくは子供」「より上等の船室の乗客」ほど生き残りやすかった、というえげつない事実が分かります。
また{mvpart}以外にも例えば{C50}など、決定木 / 回帰木のRパッケージは数多くあるので*5、色々試してみると良いでしょう。
サポートベクターマシン(SVM)
言わずと知れた、スパム判定などで重宝される非常に有名な機械学習分類器です。一般にはスパムフィルタなどバックエンドシステムで使うものですが、その汎化性能の高さを生かして例えば「先月のUUが今月定着or離脱したか否かというデータから、今月のUUが来月定着or離脱するかどうかを予測する」なんてこともできます。
RにはSVMを実装しているパッケージがいくつかありますが、まず最初に{e1071}パッケージを紹介します。これはC++, Pythonなど他言語で有名なSVMライブラリとして知られるLIBSVMのR移植版で、他言語での計算結果との整合性を重視するならこちらがベター。サンプルデータはRではド定番の「フィッシャーのアヤメのデータ」irisです。3ラベルで分類しています。
> data(iris) > attach(iris) > > ## classification mode > # default with factor response: > model <- svm(Species ~ ., data = iris) # SVMモデル推定。Rではこれでいける > > # alternatively the traditional interface: > x <- subset(iris, select = -Species) > y <- Species > model <- svm(x, y) # これはLIBSVMオリジナルを意識した書式 > > print(model) # モデルの詳細 Call: svm.default(x = x, y = y) Parameters: SVM-Type: C-classification SVM-Kernel: radial cost: 1 gamma: 0.25 Number of Support Vectors: 51 > summary(model) Call: svm.default(x = x, y = y) Parameters: SVM-Type: C-classification SVM-Kernel: radial cost: 1 gamma: 0.25 Number of Support Vectors: 51 ( 8 22 21 ) Number of Classes: 3 Levels: setosa versicolor virginica > # test with train data > pred <- predict(model, x) > # (same as:) > pred <- fitted(model) > > # Check accuracy: > table(pred, y) y pred setosa versicolor virginica setosa 50 0 0 versicolor 0 48 2 virginica 0 2 48 > > # compute decision values and probabilities: > pred <- predict(model, x, decision.values = TRUE) > attr(pred, "decision.values")[1:4,] setosa/versicolor setosa/virginica versicolor/virginica 1 1.196203 1.091757 0.6708373 2 1.064664 1.056185 0.8482323 3 1.180892 1.074542 0.6438980 4 1.110746 1.053012 0.6781059 > > # visualize (classes by color, SV by crosses): 最後に図示 > plot(cmdscale(dist(iris[,-5])), + col = as.integer(iris[,5]), + pch = c("o","+")[1:150 %in% model$index + 1])
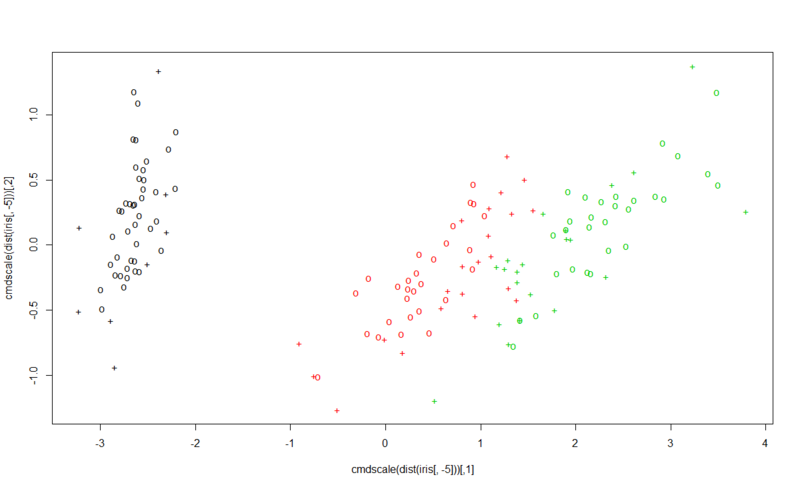
アヤメの各部位の長さのデータに基づいて、分類学上の3種類ごとに綺麗にデータが分けられることが見て取れますね。
一方、これまた有名な{kernlab}パッケージでは、以下のような感じで実行できます。上の例とは違って、こちらは2ラベルで分類しています。
> data(iris) > attach(iris) > y<-as.matrix(iris[51:150,5]) > iris1<-data.frame(iris[51:150,3:4],y) > set.seed(0) > ir.ksvm<-ksvm(y~.,data=iris1) Using automatic sigma estimation (sigest) for RBF or laplace kernel > plot(ir.ksvm,data=iris1[,1:2])
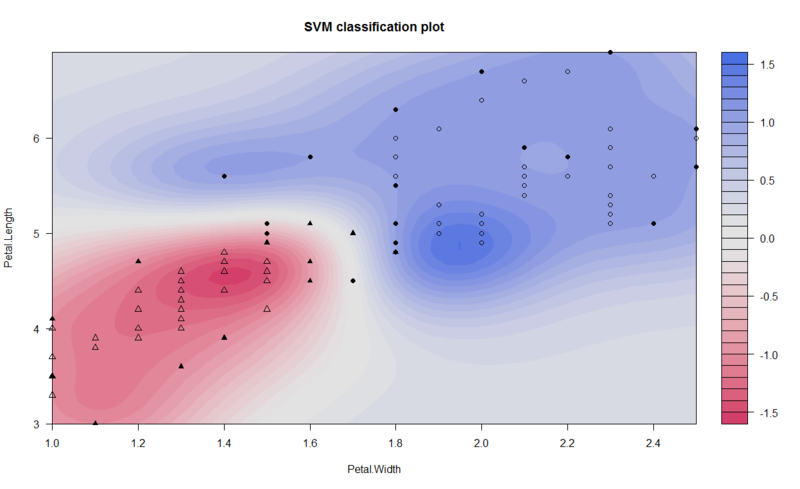
{kernlab}の方がplot()関数のカスタマイズが凝っていて見やすいかもしれません。ちなみに、変わったところでは{kernlab}には文字列分類向けの手法が実装されていて、こんな感じで試せます。
> data(reuters) > is(reuters) [1] "list" "vector" "input" "listI" "lpinput" "output" > tsv <- ksvm(reuters,rlabels,kernel="stringdot", + kpar=list(length=5),cross=3,C=10) > tsv Support Vector Machine object of class "ksvm" SV type: C-svc (classification) parameter : cost C = 10 String kernel function. Type = spectrum Hyperparameters : sub-sequence/string length = 5 Normalized Number of Support Vectors : 39 Objective Function Value : -13.6834 Training error : 0 Cross validation error : 0.02381
どちらのパッケージであっても、predict()関数もしくはそれに類似した枠組みで、学習モデルに基づいて予測することが可能です。
SVMは実装向けライブラリ・パッケージ群が非常に充実していて、例えばC++ / Java / Pythonなどの言語にも対応するライブラリが数多くあります。むしろ実務的にはそちらで実装することの方が多いかもしれないです。
ロジスティック回帰
非線形回帰分析の一種なんですが、「0 or 1に回帰させる」ことから事実上機械学習として扱われることが多いです。実際、ほとんどSVMと同じノリで使うケースが少なくないように感じます。
使い方としては、例えば「個々のユーザーIDに対して翌月定着したら1 or しなかったら0、ゲームAをプレイしたら1 or しなかったら0、ゲームBを…」という感じでカテゴリカルデータから成る素性ベクトルを作り、これを翌月定着したorしないを分類ラベルとしたロジスティック回帰にかけることで、「どのゲームがUUの翌月定着に貢献したか?」を算出することができます。
ということでRでやってみます。サンプルデータは、以前の記事で用いたtjo_uu_behavior.txtです。
> rawData <- read.delim("tjo_uu_behavior.txt") > partData<-rawData[,2:8] # UserIDカラムとResultラベルを除外する > partData<-as.matrix(partData) # マトリクス形式に直す > idx<-which(is.na(partData)==T) # NAが入っているマトリクスのインデックスを求める > partData[idx]<-0 # NAが入っているインデックス全てに0を代入する > partData<-as.data.frame(partData) # データフレーム形式に直す > attach(rawData) # 元データの各カラムを呼び出してメモリに入れる > Data<-cbind(partData,Result) # UserIDカラムを除去してNAを0に直したものとResultラベルをくっつける > detach(rawData) # 元データをメモリから外す > Data.glm<-glm(Result~.,data=Data,family="binomial") # ロジスティック回帰:"binomial"を指定する > summary(Data.glm) Call: glm(formula = Result ~ ., family = "binomial", data = Data) Deviance Residuals: Min 1Q Median 3Q Max -2.6771 -0.8263 -0.5952 0.2374 2.2293 Coefficients: Estimate Std. Error z value Pr(>|z|) (Intercept) -0.89916 0.06209 -14.483 < 2e-16 *** post.view -0.74178 0.14061 -5.275 1.33e-07 *** post.submit 4.45451 0.51088 8.719 < 2e-16 *** photo.submit 2.71624 0.30541 8.894 < 2e-16 *** comment.view -1.49874 0.28597 -5.241 1.60e-07 *** comment.submit 16.46523 438.81887 0.038 0.970 search 16.46523 403.65465 0.041 0.967 gps.on -0.09124 0.33068 -0.276 0.783 --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 (Dispersion parameter for binomial family taken to be 1) Null deviance: 2769.5 on 2200 degrees of freedom Residual deviance: 2192.1 on 2193 degrees of freedom AIC: 2208.1 Number of Fisher Scoring iterations: 14 > exp(Data.glm$coefficients)[-1] # どの変数の寄与度が強いかを出す post.view post.submit photo.submit comment.view 4.762663e-01 8.601370e+01 1.512329e+01 2.234122e-01 comment.submit search gps.on 1.415002e+07 1.415002e+07 9.127984e-01
post.submitが一番貢献度の高いアクションだということが分かります。ちなみにSVMでも同じように変数ごとの貢献度を算出することはできますが、Rだと手間がかかるようです*6。
ランダムフォレスト
近年急速に広まっている、機械学習分類器です。実はベースはただの決定木 / 回帰木なんですが、これをブートストラップ・リサンプリング法と組み合わせることで高速かつ正確に分類結果が得られるようにしたものです。
しかも、決定木のチャームポイントだった「どの変数が重要か?」を(SVMとは異なり)ストレートに求めることも可能です*7。なので、「特に未来予測したいわけではないけどどのサービスを使ってもらうと翌月定着するユーザーが増えるか?」みたいなニーズにはぴったりの手法だとも言えます。
Rでは{randomForest}パッケージを使います。データはロジスティック回帰で利用したtjo_uu_behavior.txtを引き続き用います。
> Data.rf<-randomForest(Result~.,data=Data) # 書式は回帰分析と同じ > Data.rf$importance # 変数重要度を表示する MeanDecreaseGini post.view 15.7243759 post.submit 104.0053984 photo.submit 44.4120623 comment.view 12.5603316 comment.submit 6.6833694 search 8.5228646 gps.on 0.2429852
SVMと同じく、post.submitが最も貢献度の高いアクションであるという結果になりました。
ただし、この「変数重要度」(importance)はその「向き」(定着させたor離脱させた)までは分からないので、別の方法と組み合わせる必要があります。また、計算負荷が結構でかくて、「ロジスティック回帰なら回るけどランダムフォレストだと回らない」こともあります。要注意。
なお、当然ながらランダムフォレストでもSVM同様にpredict()関数を用いて「予測」を行うことが可能です。データの性質次第でSVMとランダムフォレストとで予測精度が変わることがあるので、事前に性能比較しておくことをお薦めします。
アソシエーション分析(バスケット分析・相関ルール抽出)
いわゆる「バスケット分析」です。アメリカで有名になった「ビールとオムツのまとめ買い」の例のように、従来はどちらかというとPOSなど小売店での顧客購買データに用いられることが多かったようです。
ところが、webデータ分析の世界でも例えば「登録翌月も来訪してくれたユーザーで、コンテンツAを見ていた人は他にコンテンツB-Zのうちどれを一番多く見ていたか?」みたいな、「サービスを合わせ技で提供することでよりリピートしやすくなる」行動パターンの抽出に使われることが増えてきているようです。
ということで、これもRでやってみます。{arules}{arulesViz}パッケージを使いましょう。サンプルデータは、ベタですがGroceriesです。
> data(Groceries) > data.ap<-apriori(Groceries) # Aprioriアルゴリズムでアソシエーション・ルールを算出する parameter specification: confidence minval smax arem aval originalSupport support minlen 0.8 0.1 1 none FALSE TRUE 0.1 1 maxlen target ext 10 rules FALSE algorithmic control: filter tree heap memopt load sort verbose 0.1 TRUE TRUE FALSE TRUE 2 TRUE apriori - find association rules with the apriori algorithm version 4.21 (2004.05.09) (c) 1996-2004 Christian Borgelt set item appearances ...[0 item(s)] done [0.00s]. set transactions ...[169 item(s), 9835 transaction(s)] done [0.00s]. sorting and recoding items ... [8 item(s)] done [0.00s]. creating transaction tree ... done [0.00s]. checking subsets of size 1 2 done [0.00s]. writing ... [0 rule(s)] done [0.00s]. creating S4 object ... done [0.00s]. > data.ap<-apriori(Groceries,parameter=list(support=0.001)) # デフォルトだと条件が厳し過ぎてルールが出てこないので、条件を緩くしてみる parameter specification: confidence minval smax arem aval originalSupport support minlen 0.8 0.1 1 none FALSE TRUE 0.001 1 maxlen target ext 10 rules FALSE algorithmic control: filter tree heap memopt load sort verbose 0.1 TRUE TRUE FALSE TRUE 2 TRUE apriori - find association rules with the apriori algorithm version 4.21 (2004.05.09) (c) 1996-2004 Christian Borgelt set item appearances ...[0 item(s)] done [0.00s]. set transactions ...[169 item(s), 9835 transaction(s)] done [0.00s]. sorting and recoding items ... [157 item(s)] done [0.00s]. creating transaction tree ... done [0.00s]. checking subsets of size 1 2 3 4 5 6 done [0.01s]. writing ... [410 rule(s)] done [0.00s]. creating S4 object ... done [0.00s]. > summary(data.ap) # サマリーを見てみる set of 410 rules rule length distribution (lhs + rhs):sizes 3 4 5 6 29 229 140 12 Min. 1st Qu. Median Mean 3rd Qu. Max. 3.000 4.000 4.000 4.329 5.000 6.000 summary of quality measures: support confidence lift Min. :0.001017 Min. :0.8000 Min. : 3.131 1st Qu.:0.001017 1st Qu.:0.8333 1st Qu.: 3.312 Median :0.001220 Median :0.8462 Median : 3.588 Mean :0.001247 Mean :0.8663 Mean : 3.951 3rd Qu.:0.001322 3rd Qu.:0.9091 3rd Qu.: 4.341 Max. :0.003152 Max. :1.0000 Max. :11.235 mining info: data ntransactions support confidence Groceries 9835 0.001 0.8 > data.ap2<-subset(data.ap,subset=size(items)<4) # 多過ぎるので、試しに4つ未満の組み合わせに絞る > summary(data.ap2) set of 29 rules rule length distribution (lhs + rhs):sizes 3 29 Min. 1st Qu. Median Mean 3rd Qu. Max. 3 3 3 3 3 3 summary of quality measures: support confidence lift Min. :0.001017 Min. :0.8000 Min. : 3.131 1st Qu.:0.001118 1st Qu.:0.8125 1st Qu.: 3.261 Median :0.001220 Median :0.8462 Median : 3.613 Mean :0.001473 Mean :0.8613 Mean : 4.000 3rd Qu.:0.001729 3rd Qu.:0.9091 3rd Qu.: 4.199 Max. :0.002542 Max. :1.0000 Max. :11.235 mining info: data ntransactions support confidence Groceries 9835 0.001 0.8 > inspect(head(sort(data.ap2,by="support"),n=10)) # 上位10件の組み合わせを出してみる lhs rhs support confidence lift 1 {hamburger meat, curd} => {whole milk} 0.002541942 0.8064516 3.156169 2 {herbs, rolls/buns} => {whole milk} 0.002440264 0.8000000 3.130919 3 {tropical fruit, herbs} => {whole milk} 0.002338587 0.8214286 3.214783 4 {liquor, red/blush wine} => {bottled beer} 0.001931876 0.9047619 11.235269 5 {yogurt, rice} => {other vegetables} 0.001931876 0.8260870 4.269346 6 {herbs, shopping bags} => {other vegetables} 0.001931876 0.8260870 4.269346 7 {pork, butter milk} => {other vegetables} 0.001830198 0.8571429 4.429848 8 {yogurt, cereals} => {whole milk} 0.001728521 0.8095238 3.168192 9 {meat, margarine} => {other vegetables} 0.001728521 0.8500000 4.392932 10 {hamburger meat, bottled beer} => {whole milk} 0.001728521 0.8095238 3.168192 > plot(data.ap2,method="graph",control=list(type="items",arrowSize=0.1),interactive=T) Loading required package: tcltk Tcl/Tkインターフェースのロード中 終了済 # インタラクティブなグラフ表示にしてみる
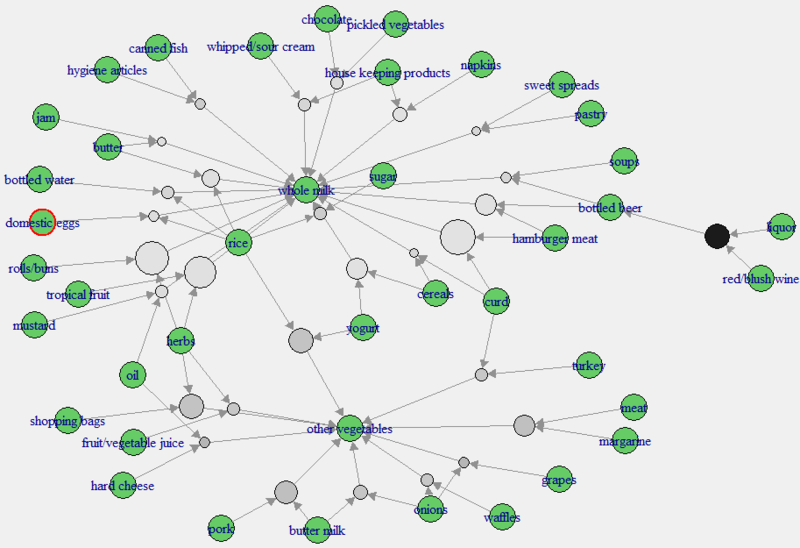
「ミルク」と「その他野菜」がえらく強いですね(笑)。。。当たり前っちゃ当たり前なんですが。こういう小売系のデータだと意外性のある発見って多くないんでしょうが、これがwebデータ分析だと想像だにしなかったような結果が得られることもあるので、個人的にはwebデータ分析向けに強く推したい手法の一つです。
ところで、この{arules}パッケージで用いているアソシエーション・ルールの算出方法は、実はレコメンドアルゴリズムのそれとよく似ています。実際、{recommenderlab}というレコメンドのシミュレーションパッケージは、{arules}を依存パッケージとして指定しているんですね。なので、アソシエーション分析を行うことで、アドホックで手動でレコメンドしていることになるとも言えそうです。
計量時系列分析
実はこれがwebデータ分析業界にとっては鬼門。僕の知る限りでは、この計量時系列分析を積極的にデータサイエンスの実務に投入しているところはまだ殆どないからです。
以前のブログ記事(見せかけの回帰について)でも数理的な基礎も含めてチラっと触れましたが、時系列データをモデリングして予測に役立てることは非常に有益です。今回の記事では、あくまでもさわりの部分だけちょろっとやってみることにします。
まず単変量時系列データについて。Rでは{forecast}パッケージが便利です。
> x.ts<-arima.sim(list(order=c(2,1,1),ar=c(0.2,-0.1),ma=0.1),n=200) # ARIMA(2,1,1)過程を200点発生させる > x.arima<-auto.arima(x.ts,trace=T,stepwise=T) # 発生させたx.ts系列のARIMA次数を推定する ARIMA(2,1,2) with drift : 572.951 ARIMA(0,1,0) with drift : 596.7827 ARIMA(1,1,0) with drift : 574.314 ARIMA(0,1,1) with drift : 570.8908 ARIMA(1,1,1) with drift : 571.74 ARIMA(0,1,2) with drift : 572.8034 ARIMA(1,1,2) with drift : 572.3238 ARIMA(0,1,1) : 569.8922 ARIMA(1,1,1) : 570.9663 ARIMA(0,1,0) : 596.6043 ARIMA(0,1,2) : 571.7132 ARIMA(1,1,2) : 571.3888 Best model: ARIMA(0,1,1) # 意外とAR次数とMA次数の推定は曖昧だったりする > plot(forecast(x.arima,level=c(50,95),h=50)) # forecast()関数で未来予測
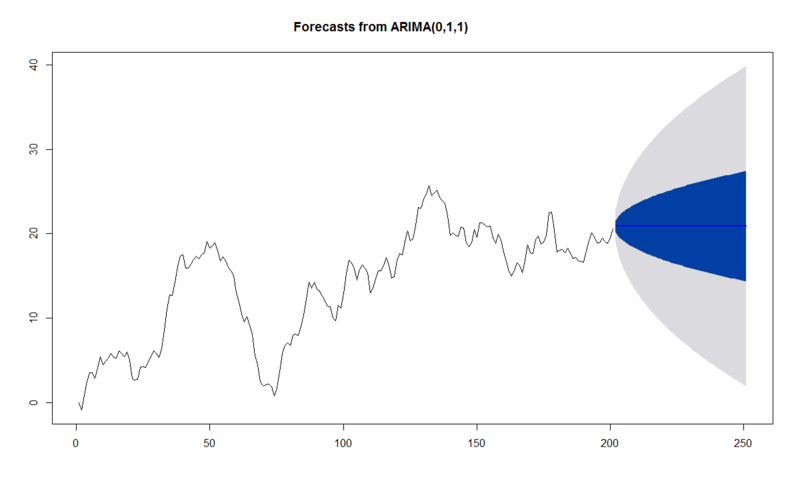
また、多変量時系列モデルであるVARモデルを使えば、互いに影響を及ぼし合うと予想される複数の時系列データ同士のインタラクションを考慮して、同時にそれらの複数の時系列データに対する未来予測を行うこともできます。ここでは{vars}パッケージを用います。サンプルデータは同梱のCanadaです。
> data(Canada) > VARselect(Canada) # VARモデル次数を推定 $selection AIC(n) HQ(n) SC(n) FPE(n) 3 2 1 3 $criteria 1 2 3 4 5 6 7 8 AIC(n) -6.191599834 -6.621627919 -6.709002047 -6.512701777 -6.30174681 -6.194596715 -6.011720944 -6.054479536 HQ(n) -5.943189052 -6.174488511 -6.063134014 -5.668105118 -5.25842152 -4.952542805 -4.570938409 -4.414968375 SC(n) -5.568879538 -5.500731387 -5.089929279 -4.395452772 -3.68632157 -3.080995238 -2.399943231 -1.944525586 FPE(n) 0.002048239 0.001337721 0.001237985 0.001534875 0.00195439 0.002278812 0.002924622 0.003073249 9 10 AIC(n) -5.912126222 -5.867271844 HQ(n) -4.073886435 -3.830303432 SC(n) -1.303996035 -0.760965421 FPE(n) 0.004015164 0.004961704 > Canada.var<-VAR(Canada,p=3) # VARモデルを推定 > Canada.pred<-predict(Canada.var,n.ahead=20,ci=0.95) # 20期先まで短期予測 > plot(Canada.pred)
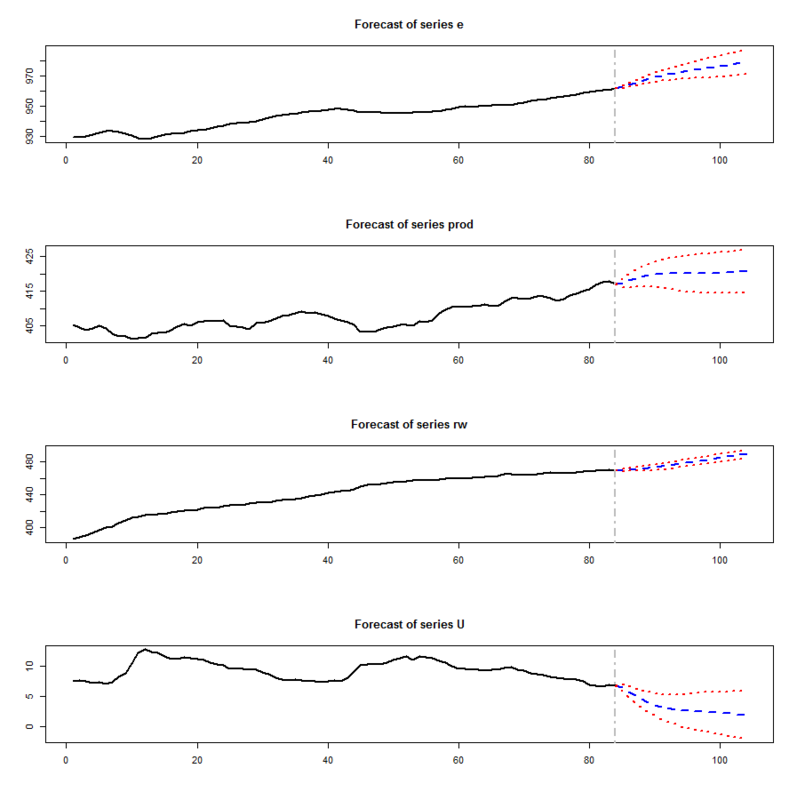
4つの時系列それぞれの未来予測が得られています。基本的にwebデータ分析におけるKPIも他の変量からの影響を受けやすいので、できるだけVARモデル以下多変量時系列モデルを用いた方が良いと僕は考えています。
これ以外にも、因果性検定や見せかけの回帰、共和分やGARCH、はたまたマルコフ転換モデルといった様々な概念・手法が計量時系列分析にはありますが、それらはまた改めて紹介しますよということで。
おわりに
今回は全部Rメインでやってみましたが、大半の手法はSPSSなどでも実装されています*8。また、実際にバックエンドシステムに組み込んだり自動化することを考えれば、Pythonなどで組めた方が良いという部分もあります。勿論、既存のパッケージ・ライブラリでは飽きたらず、自主研究開発する必要に迫られることもあるでしょう。
というわけでこの記事を「入口」として、めくるめくwebデータ分析&データサイエンスの世界に踏み入ってくれる人が一人でも増えれば嬉しいです。
おまけ1:「素性ベクトル+分類ラベル」なるデータ前処理
以前の記事(Hiveで生テーブルを取ってくる→素性ベクトル+分類ラベルのテーブルに直す)をご参照のこと。これがないと、特にRの場合は機械学習はどの手法であってもやりづらいです。
ちなみに、実はHadoop + Hiveであっても直接「素性ベクトル+分類ラベル」になるようなデータを抽出することが可能です*9。この場合、エクスポートしたデータを直接Rに読み込ませるだけでデータ分析できるので便利です。
おまけ2:グラフ理論*10
ところで、アソシエーション分析のデータはグラフ理論のグラフとして扱うこともできます。これに限らず、今後はwebデータ分析でもグラフ理論が活躍する場面は増えてくるだろう。。。というのが僕の観測です。
ぶっちゃけ僕はここは素人なので*11、はっきり言ってRのパッケージ群を使いながらだましだまし独学しているレベルです(笑)。とは言え、例えばマルコフ過程っぽく「とにかく直前と現在とのステータスの遷移にしか興味を持たない」とか仮定すると、webデータからでもちょっとしたグラフ構造を構成することができるので、色々応用できるんじゃないかと思ってます。
Rでグラフ理論をやるのであれば、以下のページが最も参考になるかと。
ちなみに{igraph}パッケージではGoogleページランクを構成するアルゴリズムの一つであるPage Rankを算出することができ、{igraph0} + {linkcomm}パッケージの組み合わせではネットワーク内に存在する下位ネットワークを検出することも可能です。
{igraph}パッケージでグラフ分析
こちらのページに非常に良いサンプルがあったので、拝借します。これはあるTwitterアカウントのツイートの単語文書行列です。
> load("termDocMatrix.rdata") > # change it to a Boolean matrix > termDocMatrix[termDocMatrix>=1] <- 1 > # transform into a term-term adjacency matrix > termMatrix <- termDocMatrix %*% t(termDocMatrix) > # inspect terms numbered 5 to 10 > termMatrix[5:10,5:10] Terms Terms data examples introduction mining network package data 53 5 2 34 0 7 examples 5 17 2 5 2 2 introduction 2 2 10 2 2 0 mining 34 5 2 47 1 5 network 0 2 2 1 17 1 package 7 2 0 5 1 21 > # build a graph from the above matrix > g <- graph.adjacency(termMatrix, weighted=T, mode = "undirected") > # remove loops > g <- simplify(g) > # set labels and degrees of vertices > V(g)$label <- V(g)$name > V(g)$degree <- degree(g) > # set seed to make the layout reproducible > set.seed(3952) > layout1 <- layout.fruchterman.reingold(g) > plot(g, layout=layout1)
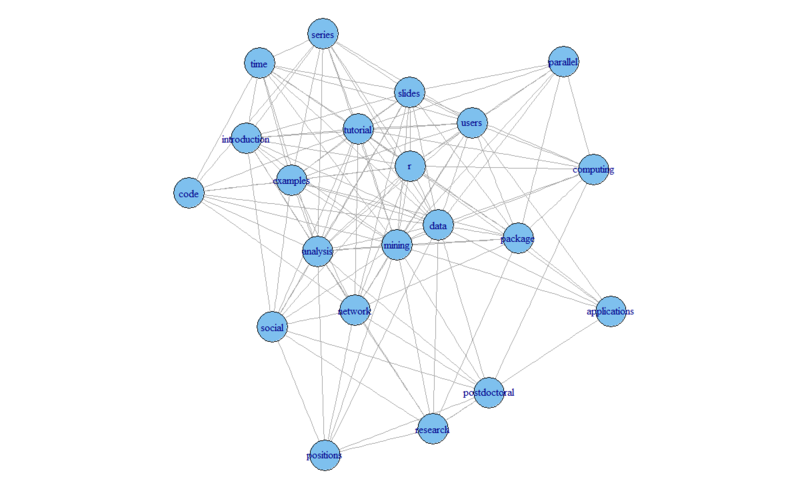
Fruchterman-Reingoldアルゴリズムで描画した結果です。中心に"data", "mining", "r"が来ていますね。このアルゴリズムだとある程度隣接しているもの同士が近くに配置されるので、この3つの単語はかなり関連性が強いであろうことがうかがえます。
Page Rankもこんな感じで出せます。"r"と"data"が強いですね。
> page.rank(g)$vector analysis applications code computing data examples 0.07022298 0.02249946 0.02695463 0.02793215 0.10116822 0.04917196 introduction mining network package parallel positions 0.02421137 0.09600309 0.04951537 0.04624544 0.02615590 0.02472511 postdoctoral r research series slides social 0.02990285 0.14125478 0.02646251 0.03275173 0.03787469 0.03888708 time tutorial users 0.03275173 0.04198358 0.05332538
他にもbetweenessとかcentralityとか色々グラフ全体の性質を表す特徴量を算出することも可能ですが、ここでは割愛します。
{linkcomm}パッケージで下位ネットワーク検出
これまではよくあるグラフ分析の話でした。ここから先は、最近になって研究開発が進められている「グラフからさらに下位のネットワークorグルーピング」を検出するという方法論のお話です。上記ページでも紹介されている通り、{linkcomm} + {igraph0}パッケージで実際に分析することができます。
例えば{linkcomm}パッケージに入っているサンプルデータ、karate*12を用いるとこんな感じになります。
> karate.g<-getLinkCommunities(karate,directed=T) Checking for loops and duplicate edges... 100.00% Calculating edge similarities for 78 edges... 100.00% Hierarchical clustering of edges... Calculating link densities... 100.00% Maximum partition density = 0.1632479 Finishing up...4/4... 100.00% Plotting... Colouring dendrogram... 100% > karate.ocg<-getOCG.clusters(karate) Calculating Initial class System....Done Nb. of classes 24 Nb. of edges not within the classes 13 Number of initial classes 24 Running.... Remaining classes: None Reading OCG data... Extracting cluster sizes... 100% > plot(karate.g) > plot(karate.g,type="graph") Getting node community edge density...100% Getting node layout... Constructing node pies...100% > plot(karate.ocg,type="graph") Getting node community edge density...100% Getting node layout... Constructing node pies...100%
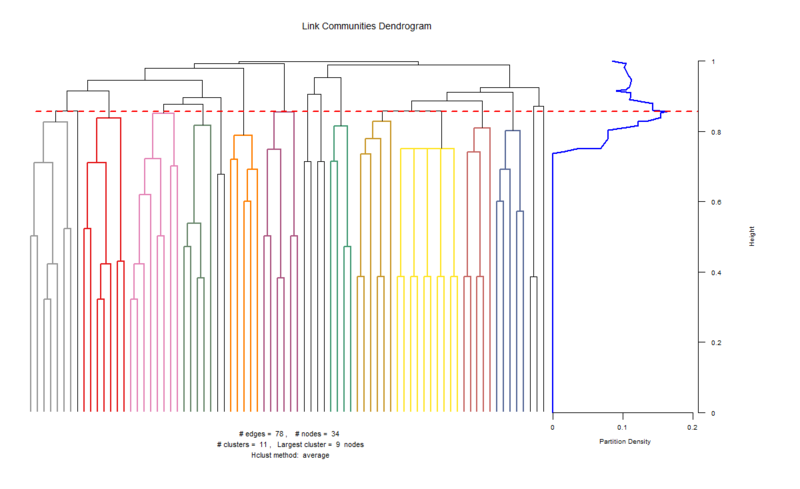
getLinkCommunities()関数を実行した時点で、デンドログラムが表示されます。このプロットからは下位ネットワークへの分岐の様子が見て取れます。また、その下の2つのplot()関数で以下のように下位ネットワークを図示することができます。

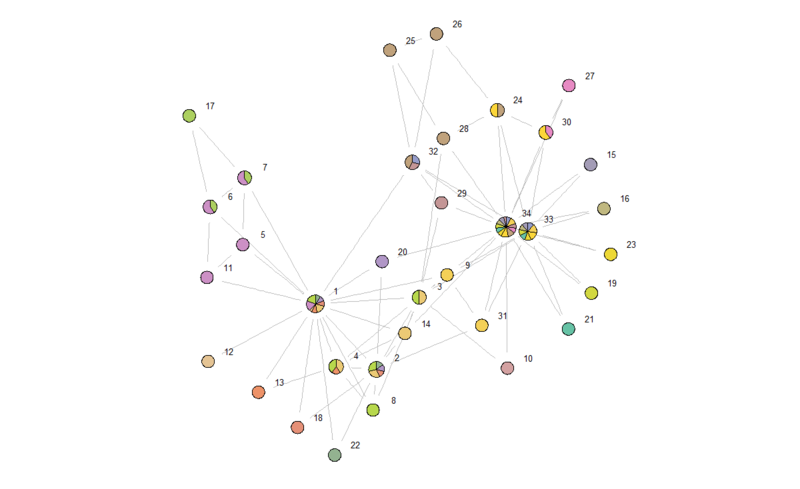
この空手クラブが、2つの大きな派閥グループに分かれていることが定性的に分かります。。。格闘技の団体でこういう派閥があるのって危ないと思うんですが(笑)。同様のデータセットを抽出することさえできれば、もちろんwebデータ分析でも十分に使える手法だと思います。
(※※用語の誤りがいくつかあったので直しました。ごめんなさい。。。)
(※※※id:yag_aysさんのご指摘に従い、グラフ理論周りは記述を改めました。ご指摘有難うございました&ごめんなさい)
*1:線がところどころ飛んでいるのは欠測値としてNAが入っているせいです
*2:Rだと可能なモデルをある程度網羅的に試せて、さらにAICとかで最適モデルを選べる
*3:一応ミシガン州の名誉のために書いておくと、近年になって特にシカゴ近辺は汚名返上とばかりに治安の向上が進み、今やシカゴのダウンタウンは夜でも女性の独り歩きができるくらい安全な街になっています。念のため
*4:厳密にはジニ係数を使うかエントロピーを使うかで手法が変わる
*5:3分類以上に分けられる手法を実装しているパッケージもある
*6:SPSSはモンテカルロ・シミュレーションか何かで出しに行っているようですが
*7:ジニ係数を用いるCART系列の場合、ジニ係数減少度で変数重要度を表すことが可能
*9:ってか最近これをやるHiveクエリの書き方を知った
*10:指摘を受けて修正しました
*11:素人ゆえの誤りを犯しておりましたごめんなさい
*12:"A social network of friendships between 34 members of a karate club at a US university in the 1970s (Zachary 1977)"と書いてある通り、実際のアメリカの大学の空手同好会における学生同士の関係性を取材して得たデータらしいです