機械学習は全然専門ではない僕が知ったかぶりをするのも何なので*1、もっともっと以前からそこそこやっている*2計量時系列分析の話でもしてお茶を濁してみることにします(笑)。
もうしつこ過ぎて自分でも嫌になってきたんですが(笑)、このシリーズでベースにするテキストは以下の2冊。沖本テキストとHamiltonテキストです*3。他にも良いテキストはあるんじゃないかと思いますが、ここではこの2冊をベースにしていきます。なお、ほとんど沖本テキストからの抜粋なのでお持ちの方はそちらを読んでもらった方が圧倒的に早いです、悪しからず。

経済・ファイナンスデータの計量時系列分析 (統計ライブラリー)
- 作者: 沖本竜義
- 出版社/メーカー: 朝倉書店
- 発売日: 2010/02/01
- メディア: 単行本
- 購入: 4人 クリック: 101回
- この商品を含むブログ (6件) を見る

- 作者: James D. Hamilton
- 出版社/メーカー: Princeton Univ Pr
- 発売日: 1994/01/11
- メディア: ハードカバー
- 購入: 1人 クリック: 5回
- この商品を含むブログ (8件) を見る
そもそも何故時系列データをモデリングするのか?
これって結構忘れられやすいポイントなんですが、要は「時間とともに変化するデータがあって、もしそれが何らかの『内部構造』を持っていれば、何がしかの形で定式化できるはずだ」という前提もしくは仮説がある、ということです。
様々な時系列データは、一見するとどれもランダムに上下動しているように見えます。株価は言わずと知れた代表例ですね。もちろん、このブログをお読みの皆さんの多くが興味のありそうな、DAUとか課金UU数とか、CVRとかもそうです。
もし、それらが本当にランダムなのであれば、そもそも分析する意味はほとんどないわけです。ただの乱数データは、そもそも次の値を予測すること自体が困難なのですから。。。
でも、例えば株価であればその根底に投資家たち同士の「景況感」「駆け引き」「雰囲気」といった要因がありますし、ソシャゲのDAUや課金UU数であればユーザーの「満足度」「イベントへの誘引」といった要因がありますし、オンライン広告のCVRであれば「顧客満足度」「商品訴求の強弱」といった要因があります。これらの要因が、時系列データ全体の挙動を決める内部構造を形作っているであろうことは、想像に難くないですよね。
そういった、隠れた内部構造を含めて「時系列データが持っている多様な特徴を記述できるモデルを構築する」こと(沖本本p.4)、「変数間の動学的関係を明らかにする」こと(沖本本p.4:要するに異なる時系列同士で時間変化していく相関・因果・依存関係などを導き出すこと)、そして「それらの時系列モデルに基づいて様々な経済学的・ビジネス的な仮説や理論を検証する」ことこそが、時系列分析の目的だと言って良いでしょう。
計量時系列分析で使うRパッケージ
大体のまとめがCRAN Task View: Time Series Analysisに載っているので、面倒な人は先にそちらを読んでください(笑)。というのも不親切なので、僕が普段使っているものを以下に列挙しておきます。なお、GARCHモデルなどwebデータサイエンスではあまり使われないものは割愛しました、ごめんなさい。
- {forecast}: 単変量時系列モデリング向け。ARIMA次数推定やその予測など
- {tseries]: 汎用パッケージ。単位根のADF検定など時系列の性質を調べる際に使う
- {vars}: 多変量(ベクトル)時系列モデリング向け。ズバリVARモデルやその予測、Granger因果など
- {urca}: 共和分モデリング向け。VECM推定など。{vars}の依存パッケージなので自動的に入る
- {tsDyn}: 非線形単変量時系列モデリング向け。SETARモデルなど
- {MSwM}: マルコフ状態転換モデル推定
その他にも{arfima}, {fracdiff}, {dlm}, {timsac}, {MSBVAR}なども試したことはありますが、まだ実戦投入していませんのでここでは割愛します。ってか特に{MSBVAR}は詳しい人いたら教えて下さい。。。
基礎知識:時系列データの種類、定常過程、ホワイトノイズ、自己相関etc.
はっきり言って沖本本からの丸写し*4で恐縮なんですが(笑)、大事な話なので一応書いていきます。
時系列データの種類
時間軸に沿ってただ値を並べただけのデータこそがまさに時系列データなわけですが、これは一応「原系列」と呼ばれます。何でそんな呼び名をつけるのかというと、色々理由があって分析する際に一旦何かしらの変数変換しなきゃいけないことがままあるからです。
例えばこんな感じ↓の原系列とかありそうですよね。
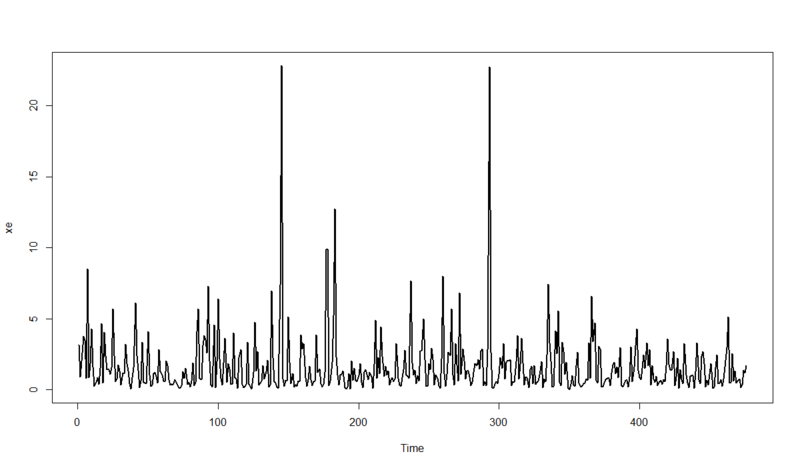
ありがちなのが、経済・ファイナンス系データで値が大きくなるとばらつきも大きくなってしまうようなもの。こういうのは扱いづらくて仕方ない*5ので、対数変換することがあります。この場合は対数系列と呼ばれます。
上の時系列を対数変換すると↓こうなります。

このブログをずっと読まれている方なら「見せかけの回帰」「共和分」といったタームを見たことがあると思いますが、そういう問題もあるので時系列分析では1時点離れたデータとの差分もよく使われます。それらを差分系列または階差系列と呼びます。
また、時系列データの水準そのものよりその変化率・成長率に興味がある場合もあって、その場合は対数差分系列(対数系列で差分を取る)が用いられることも*6。
最後に、課金額や年間売上高のような1ヶ月ごととか四季ごとといった周期性のあるデータについて。これはそのままでは分析結果が歪むので、季節調整をしなければいけません。詳しい理論は今回のシリーズ記事では省きますが、Rではこの辺を勘案して分析することももちろん可能です。その過程で季節変動を取り除いた系列は季節調整済み系列と呼ばれます。
・・・ということで色々な時系列を見てきましたが、大事なこととして「時系列データの各点は一度しか観測できないもの」だという大前提があります。その「一回性」がある以上、目の前にある時系列データ「だけ」を見ていても言えることは限られてしまいます。
そこで、計量時系列分析では得られた時系列データを、ある普遍母集団としての確率変数列
から得られたある1つの実現値とみなし、その確率変数列の生成過程に関して何らかの性質や構造を仮定する、という立場を取ります。
このような確率変数列を確率過程もしくはデータ生成過程と呼び(単に「過程」とのみ呼ぶことも多い)、その確率過程の構造を計量時系列分析では「時系列モデル」と称するわけです。
定常過程
計量時系列分析で必ず出てくるキーワードとして「定常性」というものがあります。厳密な定義は後で述べますが、平たくいえば「時間が経っても全体で見ればその時系列は変わらない」という性質のことです。これが満たされないと推定できない時系列モデルがほぼ全てなので、非常に重要な概念です*7。
定常性は同時分布*8や基本統計量の時間不変性に関するものであり、何を不変とするかによって弱定常性と強定常性の2つに分かれます。
まず、弱定常性は過程の期待値と自己共分散が時間を通じて一定である、というものです。これは想像しやすいと思います。
任意のtとkに対して、
が成立する場合、過程は弱定常といわれる
一方、強定常性は同時分布が不変である、というものです。
任意のtとkに対して、
の同時分布が同一である場合、過程は強定常といわれる
ただし同時分布が多変量正規分布の場合は正規過程と呼ばれ、弱定常性と強定常性が同値になります。
計量時系列分析のメインターゲットとなる経済データにおいては、単に定常性といったら弱定常性を指すことが多いようです。また、強定常性の仮定が必要なケースがむしろ多くないという事情もある模様です。
ホワイトノイズ
いかな何かしらの確率過程に従って得られている時系列データであったとしても、それらには何かしらの統計学的ばらつきが伴うものです。それは通常のクロスセクションデータであれば正規分布とかで表されるわけですが、時系列データの場合はホワイトノイズという系列で表されます。
各時点でのデータが互いに独立でかつ同一の分布に従う(強定常)系列はiid系列と呼ばれる。
すべての時点tにおいて
が成立するとき、
はホワイトノイズと呼ばれる。
特に正規過程に従うホワイトノイズは正規ホワイトノイズと呼ばれ、
が分散
の正規ホワイトノイズに従うことを
もしくは
と表記する
ちなみにRでこれを表現するのはめちゃくちゃ簡単で、
> w<-ts(rnorm(300)) > plot(w)

という感じに表せます。ちゃんと平均0、分散もだいたい1ぐらいでばらつきながら300点並んでいるのが見て取れるかと思います。
自己相関
非常に重要な概念です。これはもともとは自己共分散に由来する量で、例えばk時点前の値との自己共分散は
で表されますが、これは値の大きさが単位に依存してしまいます。そこでこれを基準化したものを自己相関と呼びます。
式を見ても分かりますが、要は異なる時点間でその過程が何かしらの関係性(相関)を持っているか否か?を表す指標です。なので、これが全くない(t=0以外での自己相関がゼロ)だと、単なるホワイトノイズということになってしまいます。よって、自己相関を調べることはその時系列データの性質を調べる上での第一歩だとも言えます。
Rではacf(){stats}関数で簡単に自己相関を調べることができます。例えば、
> w<-ts(rnorm(300)) > acf(w)

というようにホワイトノイズの自己相関を調べても、t=0以外の自己相関は全て統計的に有意に0から離れていない=「ない」という結果が得られます。そこで、こうしてみましょう。
> library("forecast", lib.loc="C:/Program Files/R/R-3.0.1/library") > data(gas) > acf(gas) > plot(gas)

何じゃこりゃ。めちゃくちゃ自己相関強いですね。それもそのはず、原系列をプロットすると

こうなります。これは{forecast}パッケージに同梱されているオーストラリアのガス生産量のデータで、見るからに漸増傾向&季節性が見られます。こういうデータなら、ばっちり自己相関が出るというわけです。
・・・ということで、次回からは具体的な時系列モデルをRでの扱い方と合わせて紹介していこうと思います。お楽しみに!*9
*1:新職場には正真正銘の機械学習の研究者から転じた先任のQuantitative Engineer & Researcherの人がいるので、僕なんぞが無理してやらなくても良いという構図
*2:っても実はVARとGranger因果周りが大半だったりする
*3:後者はなくても大丈夫
*4:なので持ってる人はそっち読んじゃってください!
*5:後に述べる定常性が自然と破綻してしまう
*7:なので定常性が満たされない時系列に出くわしたら、前述のように変数変換をかける羽目になることが多い
*8:ここでは同時分布の細かい説明は割愛するので、ググるなり本を読むなりして調べてください
*9:いつまで続けるか自信ないけど笑