渋谷駅前で働くデータサイエンティストのブログ

元祖「六本木で働くデータサイエンティスト」です / 道玄坂→銀座→東京→六本木→渋谷駅前

パッケージユーザーのための機械学習(4)：ニューラルネットワーク

R Python 機械学習 サンプルデータで試す機械学習シリーズ

（※はてなフォトライフの不具合で正しくない順番で画像が表示されている可能性があります）


実は僕は普段全くニューラルネットワークを使ってない上に、すぐ隣に再帰ニューラルネットワークでバリバリNIPSに通していたことのある教授氏がいるので*1、こんなところで知ったかぶりして何か書くのはほとんど蛮勇に近いんですが（笑）、純粋に自分の勉強も兼ねて分離超平面の可視化をやってみたいので頑張って書いてみようと思います。


今回の参考文献もピンクの薄い本です。第7章pp.102-113にパーセプトロン型学習規則の発展系として、誤差逆伝播法に則った多層パーセプトロン＝ニューラルネットワークの説明が載っています。


はじめてのパターン認識

はじめてのパターン認識


なのですが。改めて読み返してみると、もしかしたらはじパタの説明では実装面ではちょっとややこしいかなという気がしないでもないので、Pythonか何かで実装してみたいという人はむしろこちらを読んだ方が良いかもです。


わかりやすいパターン認識

わかりやすいパターン認識


古典中の古典ですが、こちらのpp.42-48の方が説明がシンプルで分かりやすい気がします。僕も以前Matlabでスクラッチからコード書いた時は、こちらの説明を参考にしました*2。


まずRでどんなものか見てみる


いつも通りニューラルネットワークの雰囲気だけ見るということで、前回同様GitHubに置いてある以前のサンプルデータを使いましょう。毎度お馴染み、コンバージョン(CV)に効くアクション(a1-a7)を探り出そうというテーマで用意されたデータです。dという名前でインポートしておきます。


Rでニューラルネットワークと言えば、代表的なのは{nnet}パッケージです。こいつをインストールして、以下のようにやってみましょう。

> require("nnet")
> d.nnet<-nnet(cv~.,d,size=5) # ユニット数は適当
# weights:  46
initial  value 2192.031348 
iter  10 value 537.501096
iter  20 value 508.763648
iter  30 value 500.417160
iter  40 value 496.577035
iter  50 value 491.822318
iter  60 value 490.955366
iter  70 value 489.966590
iter  80 value 489.576762
iter  90 value 488.992214
iter 100 value 488.717127
final  value 488.717127 
stopped after 100 iterations
> table(d$cv,round(predict(d.nnet,d[,-8]),0))
     
         0    1
  No  1401   99
  Yes   81 1419

# 元データに対する予測マトリクス
# 正答率94%と悪くない


前回のSVM同様、偏回帰係数とか変数重要度とかが出るような手法ではないので、至って素っ気ない結果だけが返ってきます。

ニューラルネットワークとは何ぞや


簡単に言えば「層を増やして非線形分離も可能にしたパーセプトロン」です。ちなみにパーセプトロンについては大昔の記事なんかもご参照あれ。


はじパタp.103にも書いてありますが、超絶大ざっぱに言うとパーセプトロン型学習規則は層を増やせば増やすほど、n次元のデータに対して分離超平面がn+k次元へと上がっていき*3、自由自在に分類できるようになります。層を増やすというのは、下の図で言うところの「隠れ層」(hidden layer)を入れるということです。


f:id:TJO:20131213162022p:plain:w300


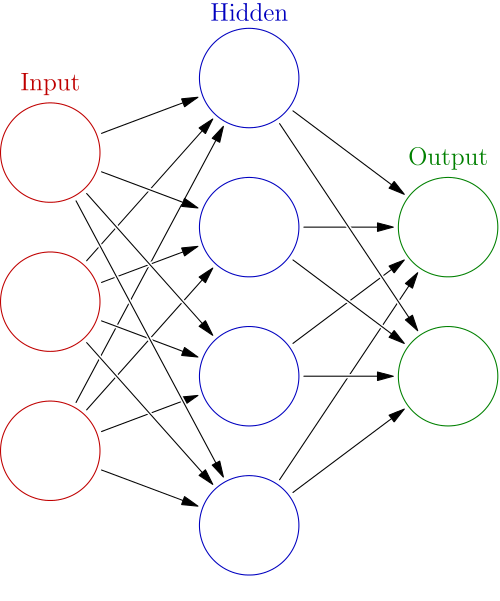
(wikipedia:en:Artificial_neural_networks)


細かい数式を全部書いていくと大変なので詳しくは上記で引用したページを見て欲しいのですが、出力関数としてシグモイド関数g(u)=\frac{1}{1+exp(-\beta u)}もしくはtanh(u)を選ぶのが通例です。理由は簡単で、出力ユニットはクラス分類値を返すので閾値を切りたいところなのですが、普通の閾値関数（ただの矩形）だと微分不可能で式が立たず、それの代用になる微分可能関数がその2つだからです。


なお、参考までにうちの教授氏が弊社公式ブログにシグモイド関数とtanh関数とでのニューラルネットワークの振る舞いの違いについて記事を書いているので、興味のある方はどぞー。


あとは、その定義に従ってコードを書いていくだけです。ちなみにWikipedia英語版にはご丁寧に擬似コードが載っています。他にも色々なブログでPRML独習の一環としてアルゴリズムの実装例が紹介されているので、興味のある方は適当に調べてみてください。

initialize network weights (often small random values)
do
forEach training example ex
prediction = neural-net-output(network, ex) // forward pass
actual = teacher-output(ex)
compute error (prediction - actual) at the output units
compute \Delta w_h for all weights from hidden layer to output layer // backward pass
compute \Delta w_i for all weights from input layer to hidden layer // backward pass continued
update network weights
until all examples classified correctly or another stopping criterion satisfied
return the network

(wikipedia:en:Artificial_neural_networks)


さすがにパーセプトロンよりは面倒ですが、SVMに比べれば*4実装自体は割と簡単だと思います。もっともここでは{nnet}を使うので実装の手間すら要りませんが（笑）。


決定境界を描いてみる


では、いつも通りやってみましょう。単純パーセプトロンとは異なり、非線形分離可能にしたのがニューラルネットワークの利点なので、XORパターンの分類をやってみましょう。GitHubからXORパターンのシンプル版、複雑版を持ってきて、それぞれxors, xorcという名前でインポートしておきます。


ところで、以前の記事（Rで機械学習するならチューニングもグリッドサーチ関数orオプションでお手軽に）で{nnet}は{caret}経由でチューニングできるというのを紹介してますので、せっかくなのでついでにやってみることにしましょう。

> require("nnet")
 要求されたパッケージ nnet をロード中です 

> xors$label<-as.factor(xors$label)
> xorc$label<-as.factor(xorc$label)
# 学習ラベルをfactor型に直す

> require("caret")
 要求されたパッケージ caret をロード中です 
 要求されたパッケージ cluster をロード中です 
 要求されたパッケージ foreach をロード中です 
foreach: simple, scalable parallel programming from Revolution Analytics
Use Revolution R for scalability, fault tolerance and more.
http://www.revolutionanalytics.com
 要求されたパッケージ lattice をロード中です 
 要求されたパッケージ plyr をロード中です 
 要求されたパッケージ reshape2 をロード中です 
# チューニングしたいので{caret}を呼ぶ

> xors.tune<-train(label~.,data=xors,method="nnet",tuneLength=4,maxit=100,trace=F)
Loading required package: class
Warning message:
executing %dopar% sequentially: no parallel backend registered 
> print(xors.tune)
100 samples
  2 predictors
  2 classes: '1', '2' 

No pre-processing
Resampling: Bootstrap (25 reps) 

Summary of sample sizes: 100, 100, 100, 100, 100, 100, ... 

Resampling results across tuning parameters:

  size  decay    Accuracy  Kappa  Accuracy SD  Kappa SD
  1     0        0.629     0.262  0.0598       0.0935  
  1     1e-04    0.662     0.306  0.0719       0.136   
  1     0.00316  0.654     0.311  0.0754       0.138   
  1     0.1      0.635     0.283  0.0603       0.101   
  3     0        0.868     0.737  0.0959       0.184   
  3     1e-04    0.905     0.813  0.0866       0.163   
  3     0.00316  0.923     0.846  0.0465       0.0912  
  3     0.1      0.918     0.837  0.0599       0.119   
  5     0        0.912     0.824  0.0671       0.128   
  5     1e-04    0.94      0.878  0.0447       0.0894  
  5     0.00316  0.952     0.904  0.026        0.0521  
  5     0.1      0.964     0.927  0.026        0.0524  
  7     0        0.928     0.854  0.044        0.0889  
  7     1e-04    0.943     0.886  0.0368       0.0731  
  7     0.00316  0.956     0.911  0.0308       0.0621  
  7     0.1      0.963     0.925  0.027        0.0542  

Accuracy was used to select the optimal model using  the largest value.
The final values used for the model were size = 5 and decay = 0.1. 
# xorsに最適なsizeとdecayが決まった

> xorc.tune<-train(label~.,data=xorc,method="nnet",tuneLength=4,maxit=100,trace=F)
> print(xorc.tune)
100 samples
  2 predictors
  2 classes: '1', '2' 

No pre-processing
Resampling: Bootstrap (25 reps) 

Summary of sample sizes: 100, 100, 100, 100, 100, 100, ... 

Resampling results across tuning parameters:

  size  decay    Accuracy  Kappa   Accuracy SD  Kappa SD
  1     0        0.563     0.129   0.0761       0.131   
  1     1e-04    0.536     0.0876  0.0748       0.134   
  1     0.00316  0.578     0.146   0.0842       0.163   
  1     0.1      0.527     0.0648  0.0855       0.15    
  3     0        0.658     0.321   0.0674       0.125   
  3     1e-04    0.663     0.332   0.0989       0.183   
  3     0.00316  0.674     0.349   0.0959       0.187   
  3     0.1      0.7       0.403   0.0798       0.155   
  5     0        0.693     0.387   0.0663       0.127   
  5     1e-04    0.696     0.391   0.0644       0.127   
  5     0.00316  0.712     0.424   0.0564       0.11    
  5     0.1      0.703     0.405   0.0694       0.137   
  7     0        0.685     0.367   0.0815       0.164   
  7     1e-04    0.679     0.358   0.0726       0.149   
  7     0.00316  0.68      0.359   0.0649       0.127   
  7     0.1      0.711     0.422   0.0624       0.124   

Accuracy was used to select the optimal model using  the largest value.
The final values used for the model were size = 5 and decay = 0.00316. 
# xorcに最適なsizeとdecayが決まった

> xors.nnet<-nnet(label~.,xors,size=5,decay=0.1)
# weights:  21
initial  value 74.105816 
iter  10 value 37.125181
iter  20 value 33.035133
iter  30 value 32.715836
iter  40 value 32.711947
iter  40 value 32.711947
iter  40 value 32.711947
final  value 32.711947 
converged
> xorc.nnet<-nnet(label~.,xorc,size=5,decay=0.00316)
# weights:  21
initial  value 81.438276 
iter  10 value 50.109105
iter  20 value 43.578750
iter  30 value 40.263447
iter  40 value 38.029642
iter  50 value 37.921192
iter  60 value 37.578741
iter  70 value 37.176696
iter  80 value 36.886196
iter  90 value 36.880551
iter 100 value 36.879125
final  value 36.879125 
stopped after 100 iterations
# それぞれnnet()関数で学習させる

> px<-seq(-3,3,0.03)
> py<-seq(-3,3,0.03)
> pgrid<-expand.grid(px,py)
> names(pgrid)<-c("x","y")
# 分離超平面を描くためのグリッドを作る

> plot(xors[1:50,-3],col="blue",pch=19,cex=3,xlim=c(-3,3),ylim=c(-3,3))
> points(xors[51:100,-3],col="red",pch=19,cex=3)
> par(new=T)
> contour(px,py,array(out.xors.nnet,dim=c(length(px),length(py))),xlim=c(-3,3),ylim=c(-3,3),col="purple",lwd=3,drawlabels=F,levels=0.5)
# シンプルパターンの分離超平面を描く

> plot(xorc[1:50,-3],col="blue",pch=19,cex=3,xlim=c(-3,3),ylim=c(-3,3))
> points(xorc[51:100,-3],col="red",pch=19,cex=3)
> par(new=T)
> contour(px,py,array(out.xorc.nnet,dim=c(length(px),length(py))),xlim=c(-3,3),ylim=c(-3,3),col="purple",lwd=3,drawlabels=F,levels=0.5)
# 複雑パターンの分離超平面を描く

> table(as.numeric(xors$label)-1,round(predict(xors.nnet,xors[,-3])))
   
     0  1
  0 49  1
  1  0 50

# シンプルパターンの正答率は99%

> table(as.numeric(xorc$label)-1,round(predict(xorc.nnet,xors[,-3])))
   
     0  1
  0 48  2
  1  9 41

# 複雑パターンの正答率は89%


f:id:TJO:20131213165858p:plain

シンプルパターンの場合と、

f:id:TJO:20131213165910p:plain

複雑パターンの場合。


SVMに比べると汎化性能という点でも色々と毛色が違うっぽい、ということがこの分離超平面を見ていても一目瞭然だと思います。この件について教授氏に質問したところ、「ニューラルネットワークは分類の追随性能ではどこまででも高められる一方で過学習に陥りやすく、職人芸的な要素が強い」「SVMは逆に汎化性能を極端に高めることで分類性能を犠牲にしている部分が大きい」とのコメントでした。


ちなみにニューラルネットワークはその性質上クラス分類事後確率を返しているのと同じことになるので、ステップ状に等高線を描くように分離超平面を描くこともできます。そうしてみると、

> plot(xors[1:50,-3],col="blue",pch=19,cex=3,xlim=c(-3,3),ylim=c(-3,3))
> points(xors[51:100,-3],col="red",pch=19,cex=3)
> par(new=T)
> contour(px,py,array(out.xors.nnet,dim=c(length(px),length(py))),xlim=c(-3,3),ylim=c(-3,3),col="purple",lwd=3,drawlabels=T)
# シンプルパターン

> plot(xorc[1:50,-3],col="blue",pch=19,cex=3,xlim=c(-3,3),ylim=c(-3,3))
> points(xorc[51:100,-3],col="red",pch=19,cex=3)
> par(new=T)
> contour(px,py,array(out.xorc.nnet,dim=c(length(px),length(py))),xlim=c(-3,3),ylim=c(-3,3),col="purple",lwd=3,drawlabels=T)
# 複雑パターン


f:id:TJO:20131213170148p:plain

シンプルパターンの場合と、

f:id:TJO:20131213170157p:plain

複雑パターンの場合。


ニューラルネットワークが、分類の易しい領域では等高線をなだらかに、分類の難しい領域ではグッと等高線の勾配をきつくして、適切にデータを分類しているのが見て取れます。


Deep learningとの関係


ところで現代におけるニューラルネットワークの発展形と言えば、言わずと知れた今や花盛りのDeep learning(wikipedia:en:Deep_learning)でしょう。名前の通り、8層とかかなり多い隠れ層を使うことで知られていますが、実際問題何がどう特徴的なのかをうちの教授氏に教わったところによると

  • Auto Encoderによる多層をまたいだ誤差伝播の改善
  • Dropoutによる過学習の抑制


だそうです。もともと過学習の抑制には正則化項を追加するという手法が知られてきたんですが*5で、先日のNIPSでは2番目のDropoutの数理的性質に関する発表があり("Understanding Dropout")、僕は新参者ゆえボサッと聞いてたので教授氏に解説してもらったところ*6「DropoutはL2ノルムと（L1ノルムで）スパース化させる効果を組み合わせたような正則化項で近似できる」*7とのことでした。信号処理系ではL1 / L2ノルムの組み合わせで折衷させる方法は割と昔からあったんですが、同じようなことがDeep learningでもいけるんですねー。


ということで、Deep learningの発展に伴い古典の山に埋もれかけていたニューラルネットワークとその関連分野の数々が今後どんどん息を吹き返してくるのは確実だと思われます。そういう意味でも、ニューラルネットワークの「性質」を理解しておくことは大事なんじゃないかなー、とぼんやり感じているところです。


最後に


そうそう、識別関数＆識別モデルまわりでは他に「判別分析」があるんですが、僕は全く使わない＆理屈はさらっと知ってる程度で解説なんて全くできないので、あえてエントリは立てません。性能比較の時にちろっと紹介する予定です。。。

*1:断っておきますが教授は実験科学系だった僕とは違ってガチの基礎数学＆機械学習系なのです

*2:ってかその時まだはじパタは出版されていなかった

*3:つまり2次元データに対して1層増やすと3次元空間中に分離超平面を描ける

*4:SMOという高い高いハードルがあるのでかなり面倒

*5:はじパタpp.109-111

*6:聞いてろよボケとか突っ込まないでー

*7:ただし実際のDropoutの実装は割と職人芸というか人海戦術でゴリゴリやるような状況なので、今後はその自動化アルゴリズムを考える必要もあるんじゃねというのがさらに教授の追加コメント