渋谷駅前で働くデータサイエンティストのブログ

元祖「六本木で働くデータサイエンティスト」です / 道玄坂→銀座→東京→六本木→渋谷駅前

Rによる最適化計画(1)：とりあえずCRAN Task Viewを見て、{linprog}パッケージのsolveLP関数とoptim関数を触ってみる

R 最適化計画

時々最適化計画をやってくれみたいな依頼をもらうことがあるんですが、普通の線形計画法って普通にやると実はwinner-take-allみたいなことになって、結局ヒトが介在しなきゃダメみたいなことになるんですよね。なーんて愚痴りながらググってたらこんなPDFを見つけまして。

最適化の結果は．．．

  • いい設定をすると
    • 往々にして，ベテランの技術者の出す結果と同じになる．
    • 当たり前の結果しか導かない


うわあああああ耳が痛ええええええってなわけで、多目的最適化とか色々漁ってる真っ最中なわけですが。単一の最適化目的関数だけ立てるからwinner-take-allになってどうしようもなくなるわけで、それに何とかして別の制約をかぶせたいなぁとか思うんですが、でも多目的最適化とかだといきなりハードル高いかなぁと。。。


というわけで、今までこのブログではあまり触れてこなかった最適化計画の話をちょっとやってみようかなと思います。ちなみに僕は最適化計画は完全にド初心者でして、明らかにテキストが必要なんですがこれがまだ決めかねており*1。。。まぁおいおい決めますよということで。


とりあえず僕が今までにインストールしている最適化計画関連のCRANパッケージは以下の通り。あとはデフォルトで入ってるoptim関数とかですかね。

  • {linprog} / 線形計画
  • {quadprog} / 凸二次計画
  • {mco} / 多目的最適化（ただしGAで解く前提）

なお言うまでもなくCRAN Task Viewを見れば網羅的に眺めることができます。

ということで、まずは備忘録的にヘルプを見てなぞった結果を下に残しておきます。いずれまともに問題を設定してやってみると思いますが、それはもう少し後でいうことで。


線形計画を{linprog}パッケージで解く


実は上にも書いたように以前から必要があって線形計画は解く機会が結構あって、基本的には{linprog}パッケージを使ってます。なのでついでにこちらの説明も。


例えば、ちょっと前のStanネタ記事でもやったようなCV数とか何かしらのKGIを広告予算とかのKPIで回帰するようなケースを考えてみましょう。この場合、CV数の純粋増加分はCV_i = a x_{1i} + b x_{2i} + c x_{3i} + dなる線形モデルで表されるわけですが、一般にはこの数字を予算配分（ポートフォリオ）を操作するだけで最大化したい！みたいな欲求があったりするわけです。


そういう場合、線形の目的関数であるCV_i = a x_{1i} + b x_{2i} + c x_{3i}に対して予算額 x_{1i}, x_{2i}, x_{3i}の制約条件を与えることで最大化するという問題に帰着するかと思います。これは僕らの世代であれば大学受験時にも勉強したであろう線形最適化問題で、2変数ならプロットを書いて考えればおしまいです。しかし実際にはもっと変数が多いので、ソルバを使うことが通常でしょう。


で、こういう場合は{linprog}パッケージのsolveLP関数を使います。ヘルプを見れば分かるかと思いますが、これの内部アルゴリズムはシンプレックス法です。wikipedia:シンプレックス法に詳細な解説があるので、それを引用すればひとまずは十分でしょう。以下引用。

  1. 線型計画問題を制限標準型に変形する。
    1. スラック変数を加え、標準型に変形する。制約条件のうち、不等式を含む物がなくなり、全て等式となる。
    2. 人工変数を加え、制限標準型に変形する。等式化された問題の目的関数をzとおく。zを最大化(最小化)する線型計画問題にする。
  2. ここまで行った作業を基にシンプレックス表(Simplex Tableau、線型計画問題の係数を表にまとめたもの)を作成する。
  3. 式の数だけ基底変数を定める。目的関数zは必ず基底変数に選ばなければならない。
  4. 初期の基底変数から得られた連立方程式の解が最適かどうかを調べる。最適とみなすことができた場合は終了。終了しなかった場合は以下の作業をおこなう。
  5. 基底変数と非基底変数の組合せを変更する。
    1. 新たに基底変数にできそうな変数を非基底変数の中から選ぶ。複数存在する場合は、最も効果の高い変数を基底に選ぶ。(ピボット列の決定)
    2. 基底から追い出す変数を決める。増加限界(定数項の値から新たに基底に入れる変数の係数を割ったもの)によって変数を決めることが多い。 (ピボット行の決定)
    3. 新しい基底変数での連立方程式を解く。具体的にはピボットを中心に掃き出し法などで新たな実行可能解を求める。実行後は4.に戻り、同様の処理を繰り返す。


ということで実際にsolveLP関数を使ってStanネタ記事の時の問題を線形計画として解いてみましょう。Stanネタ記事の時のワークスペースを参照すると、以下のような感じになっているかと思います。

> summary(ad1)
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
   0.00    0.00    0.00   12.51   38.77   52.73 
> summary(ad2)
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
   0.00    0.00    0.00   12.25   34.25   54.87 
> summary(ad3)
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
   0.00    0.00    0.00   12.44   36.40   53.54 
> c(a_w,b_w,c_w,d_w)
[1]   1.7772343   1.7304724   0.4276865 152.6054050


そこで、広告1の予算範囲を例えば30 \leq x_{1i} \leq 45、広告2は25 \leq x_{2i} \leq 40、広告3は15 \leq x_{3i} \leq 47ということにしてみましょう。その上で解くべき目的関数は推定した偏回帰係数を充てて

CV_i = 1.78x_{1i} + 1.73x_{2i} + 0.43x_{3i} + 152.7

であるとしましょう（ちなみに当然ながら切片はここでは勘案しなくて良い）。この場合、solveLP関数では以下のように回します。

> cvec<--c(a_w,b_w,c_w)
# 線形目的関数の係数を与える
# solveLP関数に限らず大半の最適化計画ソルバは「最小化」で計算するので
# 「最大化」したい場合は目的関数に-1を乗じておく（つまり係数に-1を乗じる）

> Amat<-rbind(c(1,0,0),c(1,0,0),c(0,1,0),c(0,1,0),c(0,0,1),c(0,0,1))
# 制約条件のを指定するマトリクスを与える
# これは例えばx1, x2, x3の3変数があってx1 > Aの条件だけを記述したければ
# c(1,0,0)という行を書いてやれば良い
# 次のbvecとsolveLP関数のconst.dir引数でAの値と不等式の種類を与える

> bvec<-c(30,45,25,40,15,47)
# 制約条件の定数項を与える

> cv.slt<-solveLP(cvec,bvec,Amat,const.dir=rep(c(">=","<="),3))
# solveLP関数を走らせる
# const.dirが制約条件の等号不等号を向きとともに与えるための引数

> cv.slt$solution
 1  2  3 
45 40 47 
# solutionが最適値

> cv_optimal<-a_w*cv.slt$solution[1]+b_w*cv.slt$solution[2]+c_w*cv.slt$solution[3]+d_w
# 実際に推定した最適値をモデル式に突っ込んでみる

> cv_optimal
       1 
321.9011 
# 一応これにトレンド累積値と季節成分を加えた値が本当の最適値


こんな感じで計算できます。ただ、これは皆さん想像がつくように制約条件次第でいかようにも結果が変わります。例えば制約条件を以下のように変えると。。。

> bvec2<-rep(c(0,30),3)
> cv.slt2<-solveLP(cvec,bvec2,Amat,const.dir=rep(c(">=","<="),3))
> cv.slt2$solution
 1  2  3 
30 30 30


そう、制約条件を全部同じ上限＆下限にしたら最適値も全部同じになってしまいました。これは当たり前で、結局線形計画だと単調な上下動しか最適化しないことで、シンプルに「制約条件の上限か下限に合わせる」みたいな結果になりやすいんですね。


なので、線形計画は制約条件にバリエーションがないと使い道に困ってしまうケースが結構ある印象が。。。これをどうやって改善するかについてはおいおい考えていこうかと思います。


おまけ：optim関数


Rで最適化計画といったら本来はこちらの汎用関数であるoptimを取り上げるべきなんでしょうが、実は僕はoptimは殆ど使ったことがない*2ので、代わりにRjpWikiのページへのリンクを張っておきます。



ということで、言われるがままにoptim関数のヘルプに載っている例をそのままだだ走らせてみましょう。

> ## "wild" function , global minimum at about -15.81515
> fw <- function (x)
+     10*sin(0.3*x)*sin(1.3*x^2) + 0.00001*x^4 + 0.2*x+80
> plot(fw, -50, 50, n = 1000, main = "optim() minimising 'wild function'")
> 
> res <- optim(50, fw, method = "SANN",
+              control = list(maxit = 20000, temp = 20, parscale = 20))
> res
$par
[1] -15.81517

$value
[1] 67.46774

$counts
function gradient 
   20000       NA 

$convergence
[1] 0

$message
NULL

> ## Now improve locally {typically only by a small bit}:
> (r2 <- optim(res$par, fw, method = "BFGS"))
$par
[1] -15.81515

$value
[1] 67.46773

$counts
function gradient 
      19        2 

$convergence
[1] 0

$message
NULL

> points(r2$par, r2$value, pch = 8, col = "red", cex = 2)

f:id:TJO:20141217214811p:plain


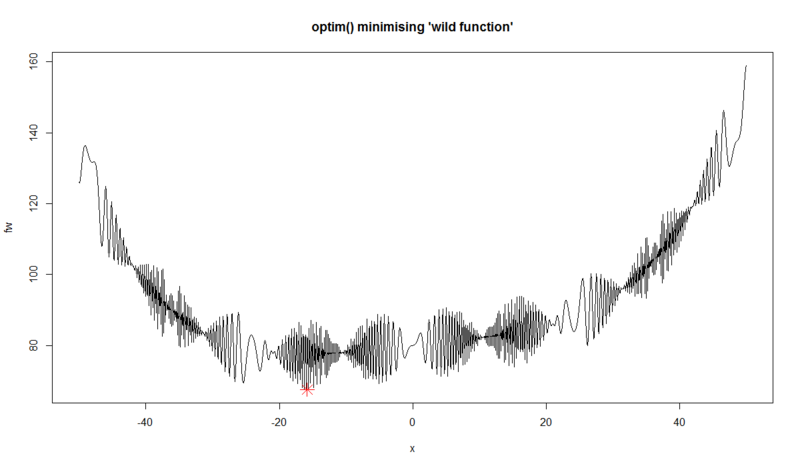
おー、ちゃんとglobal minimumに行ったわ。。。ってかなーんかこのやり方見覚えがありますよね。そう、{dlm}のdlmMLE関数で最尤推定した時のやり方です。あれも内部ではoptim関数を使っているという話だったので、いかにも納得ですね。

*1:会社の書棚には色々あるんですけどね

*2:本当にどうでもいいような最小化問題とか解くのには使いますが