基本的にロジスティック回帰は単純な線形識別関数としての分類器なので、一般には線形分離不可能パターンに対して適用すると全く分類できないという結果に終わります。実際、シンプルXORパターンと複雑XORパターンに対して、ロジスティック回帰で学習させてから決定境界を描いてみると以下のようになります。
> xors<-read.table("xor_simple.txt",header=T) > xorc<-read.table("xor_complex.txt",header=T) > xors$label<-as.factor(xors$label) > xorc$label<-as.factor(xorc$label) > xors.glm1<-glm(label~.,xors,family=binomial) # シンプルXOR > xorc.glm1<-glm(label~.,xorc,family=binomial) # 複雑XOR # グリッド作り > px<-seq(-4,4,0.03) > py<-seq(-4,4,0.03) > pgrid<-expand.grid(px,py) > names(pgrid)<-names(xors)[-3] # シンプルXORプロット > plot(c(),type='n',xlim=c(-4,4),ylim=c(-4,4)) > par(new=T) > rect(0,0,4,4,col='#aaaaff') > par(new=T) > rect(-4,0,0,4,col='#ffaaaa') > par(new=T) > rect(-4,-4,0,0,col='#aaaaff') > par(new=T) > rect(0,-4,4,0,col='#ffaaaa') > par(new=T) > plot(xors[,-3],col=c(rep('blue',50),rep('red',50)),xlim=c(-4,4),ylim=c(-4,4),pch=19,cex=2.5) > par(new=T) > contour(px,py,array(predict(xors.glm1,newdata=pgrid,type='response'),dim = c(length(px),length(py))),levels = 0.5,drawlabels = T,col='purple',lwd=3,xlim=c(-4,4),ylim=c(-4,4)) # 複雑XORプロット > plot(c(),type='n',xlim=c(-4,4),ylim=c(-4,4)) > par(new=T) > rect(0,0,4,4,col='#aaaaff') > par(new=T) > rect(-4,0,0,4,col='#ffaaaa') > par(new=T) > rect(-4,-4,0,0,col='#aaaaff') > par(new=T) > rect(0,-4,4,0,col='#ffaaaa') > par(new=T) > plot(xorc[,-3],col=c(rep('blue',50),rep('red',50)),xlim=c(-4,4),ylim=c(-4,4),pch=19,cex=2.5) > par(new=T) > contour(px,py,array(predict(xorc.glm1,newdata=pgrid,type='response'),dim = c(length(px),length(py))),levels = 0.5,drawlabels = T,col='purple',lwd=3,xlim=c(-4,4),ylim=c(-4,4))
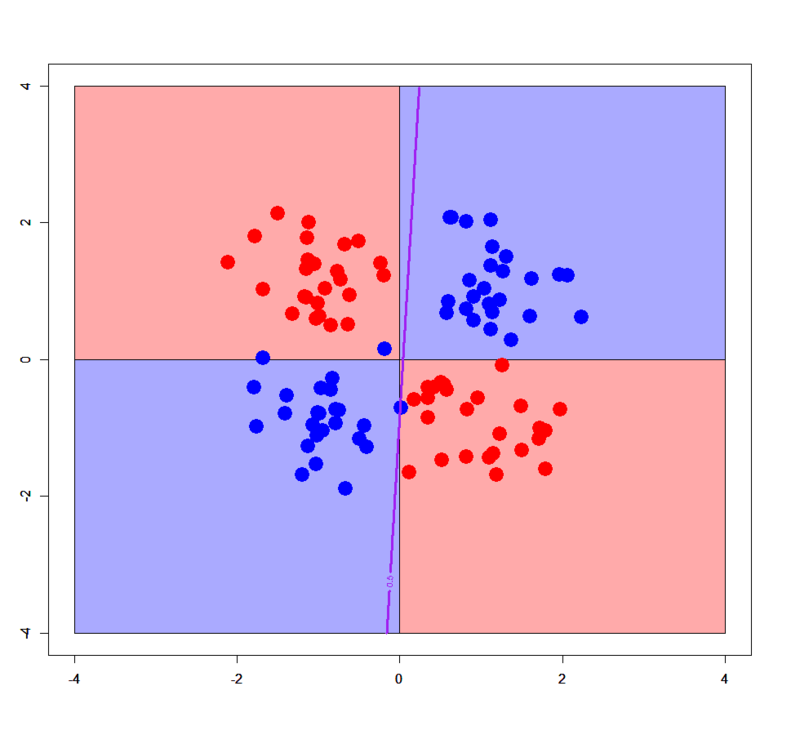
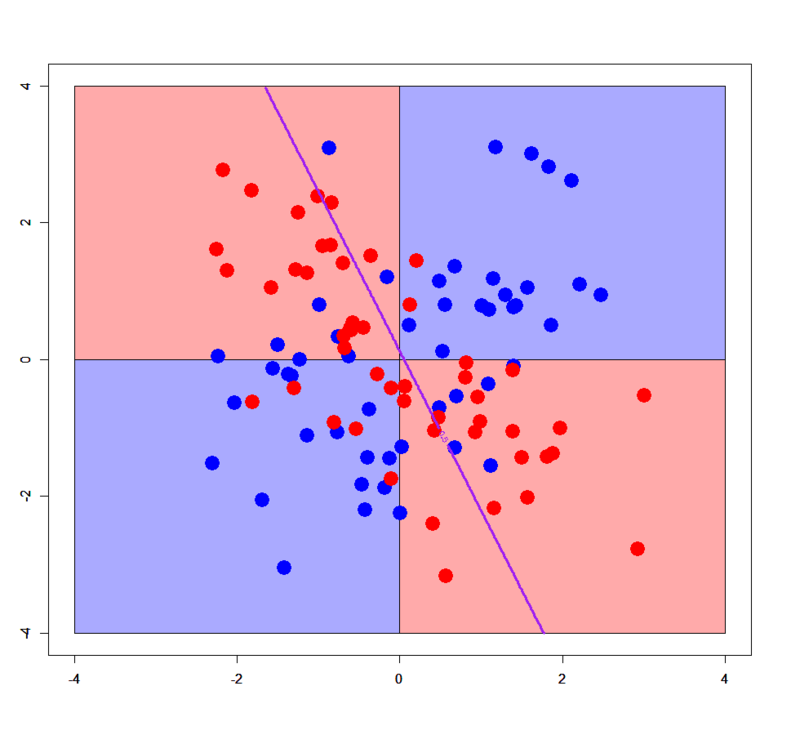
案の定ですが全然ダメです(笑)。なのですが、ここでこんなことをしてみると。。。
> xors.glm2<-glm(label~x+y+x:y,xors,family=binomial) > xorc.glm2<-glm(label~x+y+x:y,xorc,family=binomial) # シンプルXORプロット > plot(c(),type='n',xlim=c(-4,4),ylim=c(-4,4)) > par(new=T) > rect(0,0,4,4,col='#aaaaff') > par(new=T) > rect(-4,0,0,4,col='#ffaaaa') > par(new=T) > rect(-4,-4,0,0,col='#aaaaff') > par(new=T) > rect(0,-4,4,0,col='#ffaaaa') > par(new=T) > plot(xors[,-3],col=c(rep('blue',50),rep('red',50)),xlim=c(-4,4),ylim=c(-4,4),pch=19,cex=2.5) > par(new=T) > contour(px,py,array(predict(xors.glm2,newdata=pgrid,type='response'),dim = c(length(px),length(py))),levels = 0.5,drawlabels = T,col='purple',lwd=3,xlim=c(-4,4),ylim=c(-4,4)) # 複雑XORプロット > plot(c(),type='n',xlim=c(-4,4),ylim=c(-4,4)) > par(new=T) > rect(0,0,4,4,col='#aaaaff') > par(new=T) > rect(-4,0,0,4,col='#ffaaaa') > par(new=T) > rect(-4,-4,0,0,col='#aaaaff') > par(new=T) > rect(0,-4,4,0,col='#ffaaaa') > par(new=T) > plot(xorc[,-3],col=c(rep('blue',50),rep('red',50)),xlim=c(-4,4),ylim=c(-4,4),pch=19,cex=2.5) > par(new=T) > contour(px,py,array(predict(xorc.glm2,newdata=pgrid,type='response'),dim = c(length(px),length(py))),levels = 0.5,drawlabels = T,col='purple',lwd=3,xlim=c(-4,4),ylim=c(-4,4))
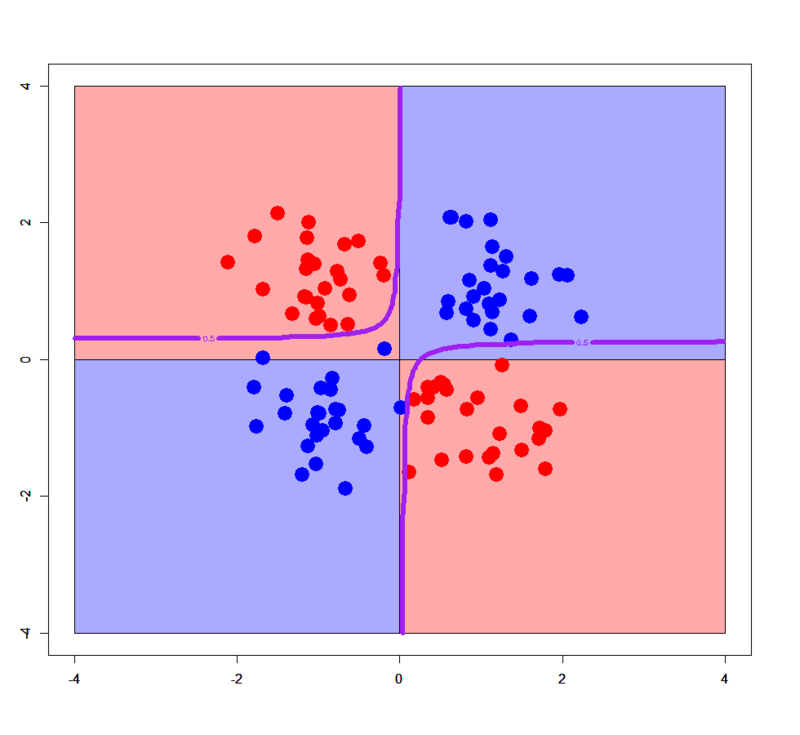
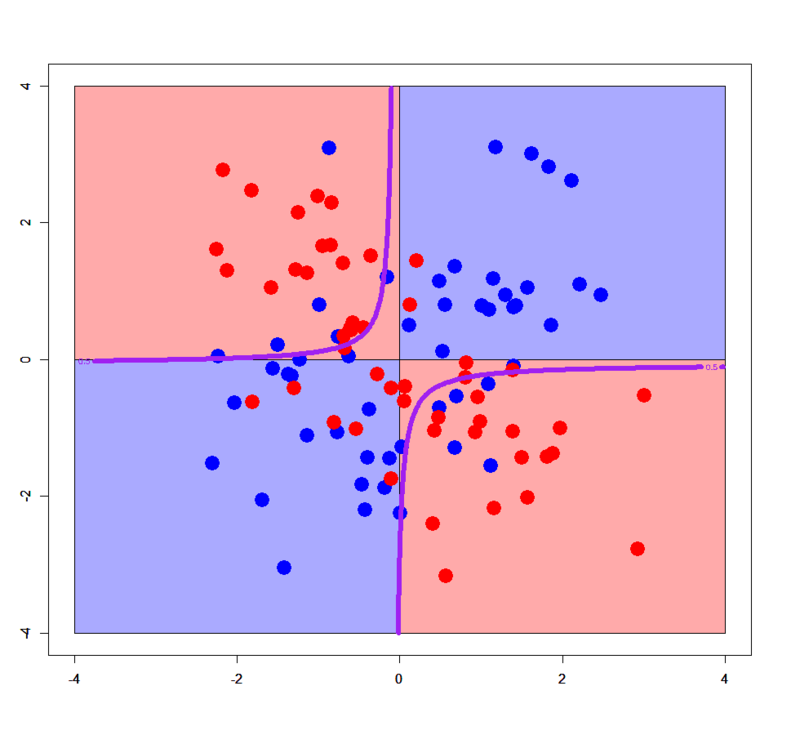
あら不思議、ガウシアンカーネル・ソフトマージンSVMで分離したかのように、きちんとXORパターンに沿った決定境界が描かれています。やったことと言えば、交互作用項x:yをformula式に入れただけ。
では、XORパターンでとして3次元プロットしたらどうなるんでしょうか。やってみれば分かりますが、
> library(scatterplot3d) > par(mfrow=c(1,2)) > scatterplot3d(xors$x,xors$y,xors$x*xors$y,color=c(rep('blue',50),rep('red',50)),pch=19,cex.symbols = 2) > scatterplot3d(xors$x,xors$y,xors$x*xors$y,color=c(rep('blue',50),rep('red',50)),pch=19,cex.symbols = 2,angle = 0) > scatterplot3d(xorc$x,xorc$y,xorc$x*xorc$y,color=c(rep('blue',50),rep('red',50)),pch=19,cex.symbols = 2) > scatterplot3d(xorc$x,xorc$y,xorc$x*xorc$y,color=c(rep('blue',50),rep('red',50)),pch=19,cex.symbols = 2,angle = 0)
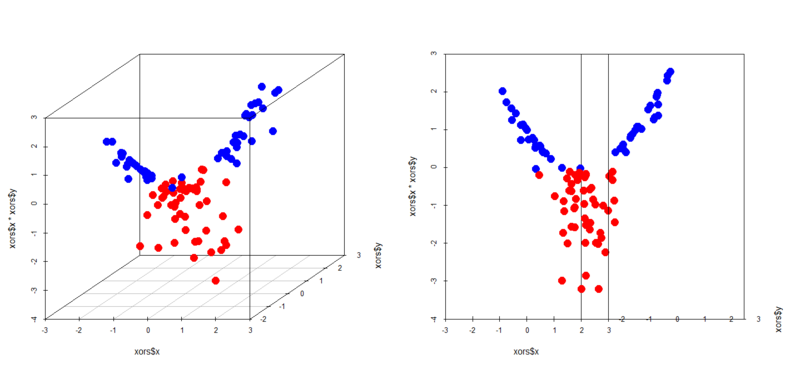
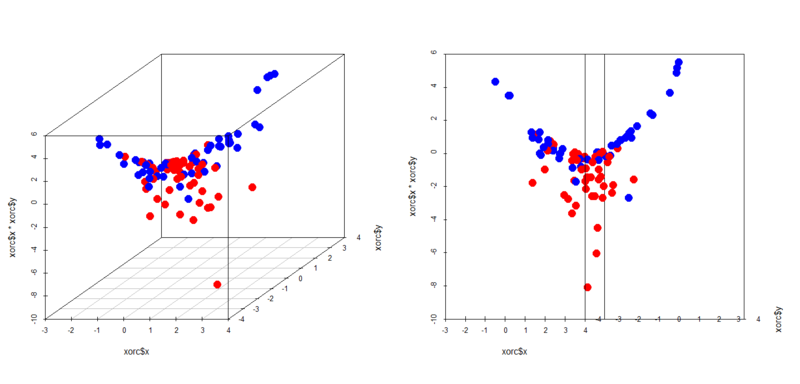
これはカーネルによる変換とよく似てますが、うまい具合に2クラスそれぞれのサンプルがなる超平面を境に上下に分かれるようになっているのが見て取れます。
ちなみに二重同心円パターンで同じことをやってみると、
> dc<-read.table("double_circle.txt",header=T) > par(mfrow=c(1,2)) > scatterplot3d(dc$x,dc$y,dc$x*dc$y,color=c(rep('blue',300),rep('red',300)),pch=19,cex.symbols = 2) > scatterplot3d(dc$x,dc$y,dc$x*dc$y,color=c(rep('blue',300),rep('red',300)),pch=19,cex.symbols = 2,angle = 0)
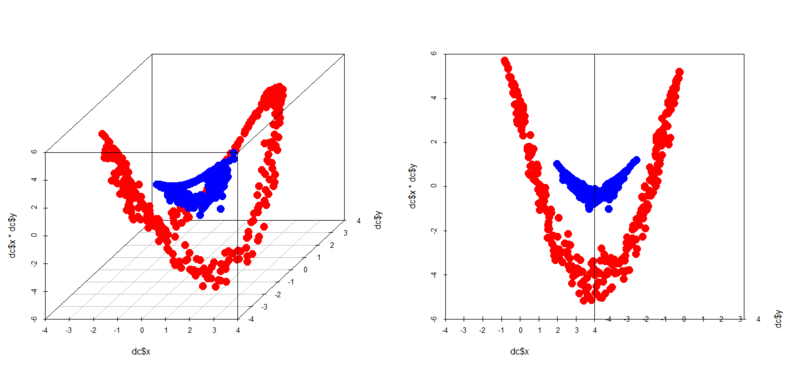
どう見ても超平面では分離できない形になりましたw もちろんロジスティック回帰やってもダメで、
> dc$label<-as.factor(dc$label) > dc.glm2<-glm(label~x+y+x:y,dc,family=binomial) > par(mfrow=c(1,1)) > plot(dc[,-3],col=c(rep('blue',300),rep('red',300)),xlim=c(-4,4),ylim=c(-4,4),pch=19,cex=2) > par(new=T) > contour(px,py,array(predict(dc.glm2,newdata=pgrid,type='response'),dim = c(length(px),length(py))),levels = 0.5,drawlabels = T,col='purple',lwd=6,xlim=c(-4,4),ylim=c(-4,4))
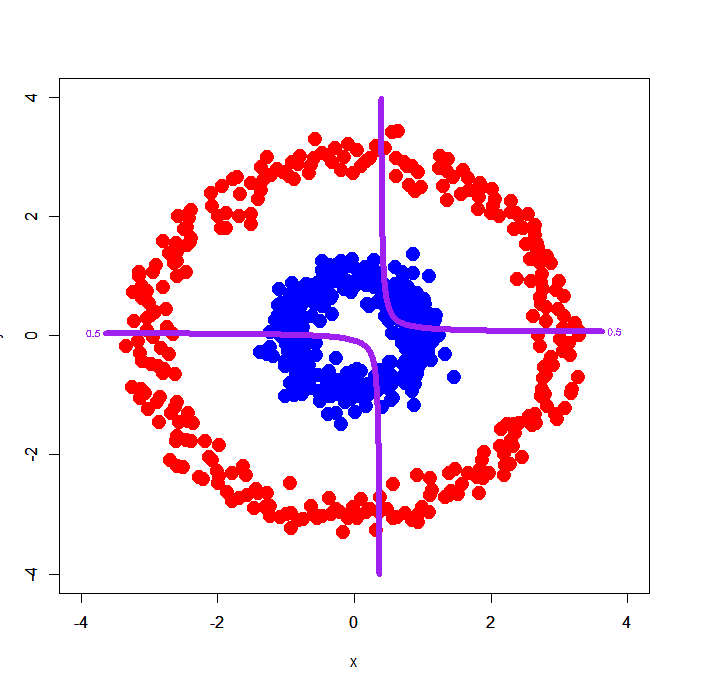
全くもってダメですw これは拙著第8章でも示したように、例えばガウシアンカーネルなどを用いればきちんと超空間上で綺麗に上下に分かれるパターンなので、ただの交互作用項では無理な相談なのでした。。。ということで参考までにガウシアンカーネルでz座標を与えたものがこちら。
> zdc<-rep(0,600) > for (i in 1:600){ + for (j in 1:600){ + zdc[i]<-zdc[i]+exp(-((dc[i,1]-dc[j,1])^2+(dc[i,2]-dc[j,2])^2)) + } + } > par(mfrow=c(1,2)) > scatterplot3d(dc$x,dc$y,zdc,color=c(rep('blue',300),rep('red',300)),pch=19,cex.symbols=1.5) > scatterplot3d(dc$x,dc$y,zdc,color=c(rep('blue',300),rep('red',300)),pch=19,cex.symbols=1.5,angle=0)
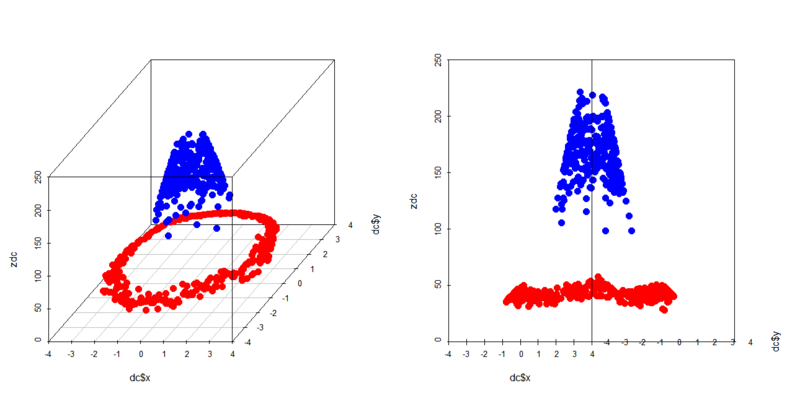
こんな感じで綺麗に上下に分かれました。見るからにあたりの超平面で完全にクラス分類できることが分かります。もちろんこれを例えばSVMで分類することは可能で、
> dc.tune<-tune.svm(label~.,data=dc,kernel='radial') > dc.tune Error estimation of ‘svm’ using 10-fold cross validation: 0 > dc.tune$best.model Call: best.svm(x = label ~ ., data = dc, kernel = "radial") Parameters: SVM-Type: C-classification SVM-Kernel: radial cost: 1 gamma: 0.5 Number of Support Vectors: 24 > dc.svm<-svm(label~.,dc,kernel='radial',cost=dc.tune$best.model$cost,gamma=dc.tune$best.model$gamma) > plot(dc[,-3],col=c(rep('blue',300),rep('red',300)),pch=19,cex=1.5,xlim=c(-4,4),ylim=c(-4,4)) > par(new=T) > contour(px,py,array(predict(dc.svm,newdata=pgrid),dim=c(length(px),length(py))),drawlabels=T,lwd=6,col='purple')
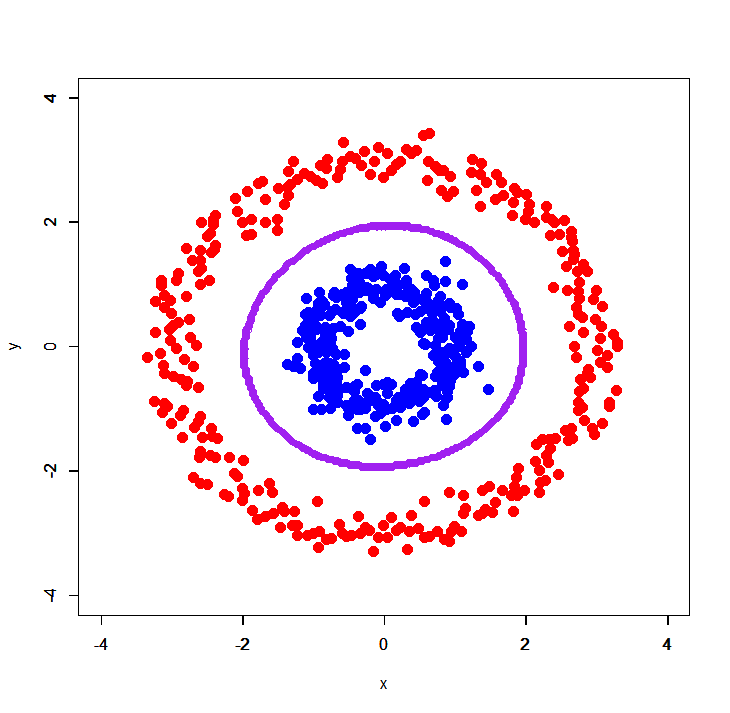
見事に分類できました。ということで、こういうパターンの時にどうすれば良いかはちょっと考えてみます。。。まぁカーネルロジスティック回帰しろ、と言われればそこまでですが(汗)。