今やKaggleやKDD cup以下名だたる機械学習コンペで絶大な人気を誇る分類器、Xgboost (eXtreme Gradient Boosting)。特にKaggleのHiggs Boson Machine Learning Challengeの優勝チームが駆使したことで有名になった感があるようで。
その実装ですが、C++ベースで高速化したものにRとPythonのラッパーをつけたものが既にGitHubで公開されています。
Rパッケージである{xgboost}のインストールについての注意事項は前回の記事に書いていますので、インストールの際はご参考にしていただければと。
さて。これだけ大人気の分類器となると国内外問わず色々な解説記事に溢れておりまして、例えば日本語ブログでもこれだけの記事が既に出てます。
- 勾配ブースティングについてざっくりと説明する - About connecting the dots.
- 最近、流行のxgboost - puyokwの日記
- xgboostとgbmのパラメータ対応一覧をつくる - 盆栽日記
- Gradient Boosting Decision Treeでの特徴選択 in R | 分析のおはなし。
既に色々な有力ブログが取り上げ切った後でこんな記事を書いてももはや何も面白くない気がするんですが、自分の備忘録のためにきちんと書いておこうかと思います。と言っても、正直言って大した内容は書けませんが。。。
まずMNISTのショートバージョンで試してみる
前回までは自前の多変量データセットを使っていたんですが、今回からは英語版ブログでも愛用しているMNISTのショートバージョンを使ってみようと思います。僕のGitHubリポジトリから"short_prac_train.csv"と"short_prac_test.csv"をDLしてきて、それぞれtrain, testという名前でインポートしておいて下さい。
> library(xgboost) > library(Matrix) > train<-read.csv("short_prac_train.csv") > test<-read.csv("short_prac_test.csv") > train.mx<-sparse.model.matrix(label~., train) > test.mx<-sparse.model.matrix(label~., test) > dtrain<-xgb.DMatrix(train.mx, label=train$label) > dtest<-xgb.DMatrix(test.mx, label=test$label) > train.gbdt<-xgb.train(params=list(objective="multi:softmax", num_class=10, eval_metric="mlogloss", eta=0.2, max_depth=5, subsample=1, colsample_bytree=0.5), data=dtrain, nrounds=150, watchlist=list(eval=dtest, train=dtrain)) [0] eval-mlogloss:1.738412 train-mlogloss:1.698857 [1] eval-mlogloss:1.445343 train-mlogloss:1.381565 [2] eval-mlogloss:1.238927 train-mlogloss:1.152097 # ...中略... [148] eval-mlogloss:0.154864 train-mlogloss:0.002696 [149] eval-mlogloss:0.155017 train-mlogloss:0.002677 > pred<-predict(train.gbdt,newdata=dtest) > sum(diag(table(test$label,pred)))/nrow(test) [1] 0.958
この0.958というスコア、実はランダムフォレストの0.953を上回り、概ねベストに近いチューニングのh2o.deeplearningと同じ数字(0.958)なんですね。KaggleのMNISTコンペではそこまでスコアは伸ばせなかったんですが、いずれにせよDeep Learningに匹敵するスコアを叩き出せるということだけはお分かりいただけるかなと。
Xgboostとは何ぞや
実はそれほど新しい手法というわけでもないので、既刊本にも結構説明が載ってます。とりあえず『はじパタ』pp.188-193とESL邦訳本『統計的学習の基礎』*1第10章pp.385-442を、ESL原典ならChapter 10 pp.337-388をAdaboostの辺りから読んでみるとよろしいかと。Web上から見られるものとしてはid:smrmktさんもご推薦のFEGさんのKDD cup 2009の解説資料が分かりやすくて良いかと思います*2。
そう言えば、Adaboostについてはこのシリーズの前回の記事で取り上げていますね(パッケージユーザーのための機械学習(11):番外編 - AdaBoost - 渋谷駅前で働くデータサイエンティストのブログ)。Xgboostも本質的にはAdaboostと発想は同じで、
ブースティング(boosting)は、与えた教師付きデータを用いて学習を行い、その学習結果を踏まえて逐次に重みの調整を繰り返すことで複数の学習結果を求め、その結果を統合・組み合わせ、精度を向上させる。
というブースティングの流れを汲むものです。Adaboostでは損失関数をとしていますが、これを決定木・回帰木など樹木モデルに替えたものがXgboostというかgradient boosted treeです。そうすることで特徴量が連続変数・カテゴリ変数であっても対応が容易で、外れ値や欠損値にも強い学習器を作ることができます。またAdaboostが各ステップで更新する際に学習データ全体を使っていたのを改め、ランダムに抽出したサンプルのみを用いている点でも異なります。この辺はランダムフォレストに発想が近いかな?という気もしますね。
ちなみに『統計的学習の基礎』pp.409-412にはもう少し細かい説明が載っています。端的に言えば元々樹木モデルをブースティングに適用したブースティング木というアルゴリズムがあり、その損失関数を最小化する木の組み合わせを求める際の最適化手法として最急降下法を用いているところを、勾配ブースティングでは各ステップで可能な限り負の勾配が得られるような木をOLSで推定して得るということをやる、みたいです*3。
『統計的学習の基礎』p.413及びFEGさんの資料にはそのものズバリ「勾配ブースティング木」のアルゴリズムが載っています。スクラッチから実装してみたい人は参考にしてみると良いでしょう。以下一部他資料を参照して修正しながら引用*4。
アルゴリズム10.3 勾配ブースティング木
1.
となるように初期化する。
である。
2.
から
に対して、以下を行う。
(a) 添え字をランダムに入れ替えた上で、
に対して次を計算する。
(b) 回帰木を目的変数
に対して回帰木を推定し、その終端領域を
とする。
(c)
に対して次を計算する。
(d)
のように更新する。
3.
を出力する。
(※筆者注:ここでは回帰木を想定、
は予測関数、
は学習データ上の
に対する損失関数、
は指示関数で
が
に含まれる場合1を返す)
2.(d)の式の更新部を単なる(a)と何かしらの学習係数との積にする(つまり)と最急降下法になるのですが、この勾配ブースティング木のアルゴリズムではより巧みな更新が行われていることが分かるかと思います。即ち、(b)のステップで検出された誤判定領域にかかるサンプルだけを抜き出して
を更新するというわけです。これで最急降下法よりもさらにgreedyに更新できるというカラクリです。
その他『統計的学習の基礎』p.413以降にはXgboostのチューニングのために必要な知識がいくつか述べられています。例えば木の大きさ(tree size)は概ね
が妥当である上に概ね6ぐらいで良かろうとか*5、繰り返し
はニューラルネットワークの早期打ち切り戦略と同じであまり大きくし過ぎるなとか、上記ステップ2.(d)の式を
として木の貢献度
を
の範囲内で小さめ(例えば0.2や0.6とか)に設定せよとか*6、部分標本化率
を0.5程度にしろとか*7、そんなことが書いてあってチューニングの参考になるかと。
なお、パラメータチューニングについては本家のGitHubにもコメントがあり、
Control Overfitting
When you observe high training accuracy, but low tests accuracy, it is likely that you encounter overfitting problem.
There are in general two ways that you can control overfitting in xgboost
- The first way is to directly control model complexity
- This include max_depth, min_child_weight and gamma
- The second way is to add randomness to make training robust to noise
- This include subsample, colsample_bytree
- You can also reduce stepsize eta, but needs to remember to increase num_round when you do so.
まぁこれはまさに書かれている通りで、「バイアス=バリアンストレードオフを考えてチューニングせよ」ってことですね。なお、Adaboost同様基本的には「誤判定した学習データに対してどんどん直列に補正していく」タイプの分類器なので、繰り返し回数を増やすほど過学習しやすくなるという点に注意が必要です。『統計的学習の基礎』p.418の図を見ると、実際に縮小率etaの値によっては繰り返し回数が増えるほど過学習が進んで精度が悪化する様子が見て取れます。
決定境界を描いてみる:XORパターン
ということで、このシリーズ恒例のXORパターンデータを使いましょう。GitHubリポジトリからシンプル版、複雑版を持ってきて、それぞれxors, xorcという名前でインポートしておきます。
{xgboost}パッケージはその他の数多くの機械学習系Rパッケージとは異なり、何故かformula式には対応していません(汗)。おそらく大規模データ対策なのだと思われますが、スパースマトリクス形式を含むマトリクス型でのデータ読み込みを基本としています。
モデルの学習に使う関数はxgboostとxgb.trainの2つがありますが、xgb.trainの方が色々調整しやすいのでお薦めです。特にテストデータ側の正解ラベルも持っていてcross validationしたい時には、xgb.train関数であればwatchlist引数を使って学習ステップごとの損失関数の変動を見てパラメータチューニングに生かすという芸当もできます。
# XORデータ読み込み > xors<-read.table("xor_simple.txt",header=T) > xorc<-read.table("xor_complex.txt",header=T) # グリッドを作る > px<-seq(-4,4,0.03) > py<-seq(-4,4,0.03) > pgrid1<-expand.grid(px,py) > names(pgrid1)<-names(xors)[-3] # パッケージをロード > library(xgboost) > library(Matrix) # 元データのラベルが良くないので直す > xors$label<-xors$label-1 > xorc$label<-xorc$label-1 # sparse.model.matrix形式に直す > xors.mx<-sparse.model.matrix(label~.,xors) > xorc.mx<-sparse.model.matrix(label~.,xorc) > pgrid1.mx<-sparse.model.matrix(~.,pgrid1) # xgb.DMatrix形式に直す > dxors<-xgb.DMatrix(xors.mx,label=xors$label) > dxorc<-xgb.DMatrix(xorc.mx,label=xorc$label) > dpgrid1<-xgb.DMatrix(pgrid1.mx) # xgboostモデルを学習させる。ここではxgb.train関数を使う記法で > xors.gbdt<-xgb.train(params=list(objective="binary:logistic",eval_metric="logloss"),data=dxors,nrounds=100) > xorc.gbdt<-xgb.train(params=list(objective="binary:logistic",eval_metric="logloss"),data=dxorc,nrounds=100) # シンプルパターン > plot(c(),type='n',xlim=c(-4,4),ylim=c(-4,4)) > par(new=T) > rect(0,0,4,4,col='#aaaaff') > par(new=T) > rect(-4,0,0,4,col='#ffaaaa') > par(new=T) > rect(-4,-4,0,0,col='#aaaaff') > par(new=T) > rect(0,-4,4,0,col='#ffaaaa') > par(new=T) > plot(xors[,-3],col=c(rep('blue',50),rep('red',50)),xlim=c(-4,4),ylim=c(-4,4),pch=19,cex=2.5) > par(new=T) > contour(px,py,array(predict(xors.gbdt,newdata=dpgrid1),dim = c(length(px),length(py))),levels = 0.5,drawlabels = T,col='purple',lwd=5,xlim=c(-4,4),ylim=c(-4,4)) # 複雑パターン > xorc.gbdt<-xgb.train(params=list(objective="binary:logistic",eval_metric="logloss"),data=dxorc,nrounds=100) > plot(c(),type='n',xlim=c(-4,4),ylim=c(-4,4)) > par(new=T) > rect(0,0,4,4,col='#aaaaff') > par(new=T) > rect(-4,0,0,4,col='#ffaaaa') > par(new=T) > rect(-4,-4,0,0,col='#aaaaff') > par(new=T) > rect(0,-4,4,0,col='#ffaaaa') > par(new=T) > plot(xorc[,-3],col=c(rep('blue',50),rep('red',50)),xlim=c(-4,4),ylim=c(-4,4),pch=19,cex=2.5) > par(new=T) > contour(px,py,array(predict(xorc.gbdt,newdata=dpgrid1),dim = c(length(px),length(py))),levels = 0.5,drawlabels = T,col='purple',lwd=5,xlim=c(-4,4),ylim=c(-4,4))

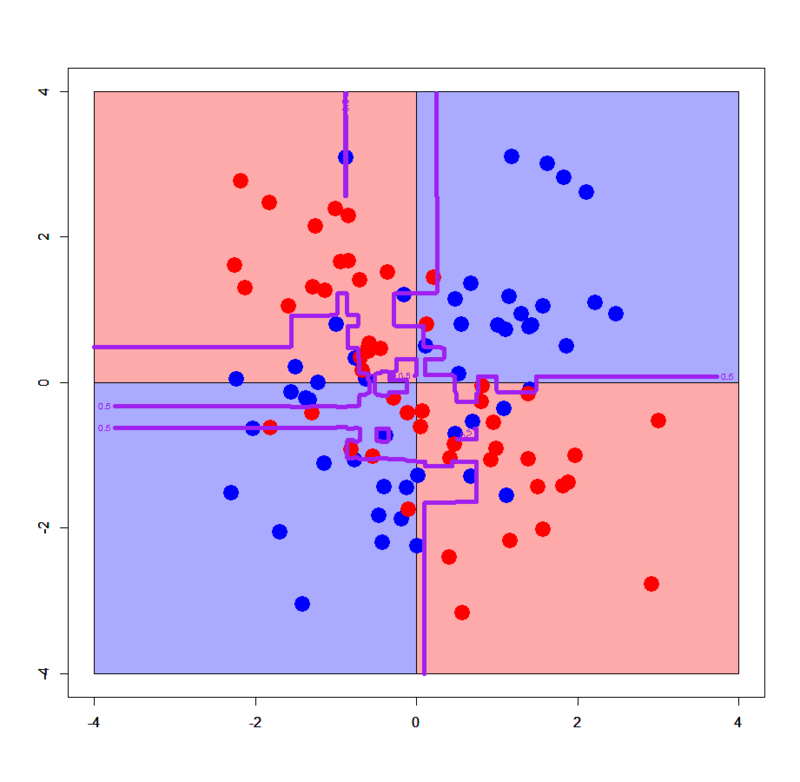
単純パターンにおける決定境界は普通の決定木と完全に同じですが、複雑パターンの方は通常の決定木より複雑な上に、以前見たランダムフォレストの決定境界とも雰囲気が異なるようです。ただしランダムフォレストの割とハチャメチャな感じに比べると、真の決定境界(プロット内の薄い赤と薄い青で塗り分けた境界)にかなり近いという印象はありますね。
次に、パラメータチューニングの影響を見てみましょう。
# ややオーバーフィッティング強め > xorc.gbdt<-xgb.train(params=list(objective="binary:logistic",eval_metric="logloss",eta=1,max_depth=8),data=dxorc,nrounds=100) > plot(c(),type='n',xlim=c(-4,4),ylim=c(-4,4)) > par(new=T) > rect(0,0,4,4,col='#aaaaff') > par(new=T) > rect(-4,0,0,4,col='#ffaaaa') > par(new=T) > rect(-4,-4,0,0,col='#aaaaff') > par(new=T) > rect(0,-4,4,0,col='#ffaaaa') > par(new=T) > plot(xorc[,-3],col=c(rep('blue',50),rep('red',50)),xlim=c(-4,4),ylim=c(-4,4),pch=19,cex=2.5) > par(new=T) > contour(px,py,array(predict(xorc.gbdt,newdata=dpgrid1),dim = c(length(px),length(py))),levels = 0.5,drawlabels = T,col='purple',lwd=5,xlim=c(-4,4),ylim=c(-4,4)) # やや汎化強め > xorc.gbdt<-xgb.train(params=list(objective="binary:logistic",eval_metric="logloss",eta=0.1,max_depth=4),data=dxorc,nrounds=100) > plot(c(),type='n',xlim=c(-4,4),ylim=c(-4,4)) > par(new=T) > rect(0,0,4,4,col='#aaaaff') > par(new=T) > rect(-4,0,0,4,col='#ffaaaa') > par(new=T) > rect(-4,-4,0,0,col='#aaaaff') > par(new=T) > rect(0,-4,4,0,col='#ffaaaa') > par(new=T) > plot(xorc[,-3],col=c(rep('blue',50),rep('red',50)),xlim=c(-4,4),ylim=c(-4,4),pch=19,cex=2.5) > par(new=T) > contour(px,py,array(predict(xorc.gbdt,newdata=dpgrid1),dim = c(length(px),length(py))),levels = 0.5,drawlabels = T,col='purple',lwd=5,xlim=c(-4,4),ylim=c(-4,4))

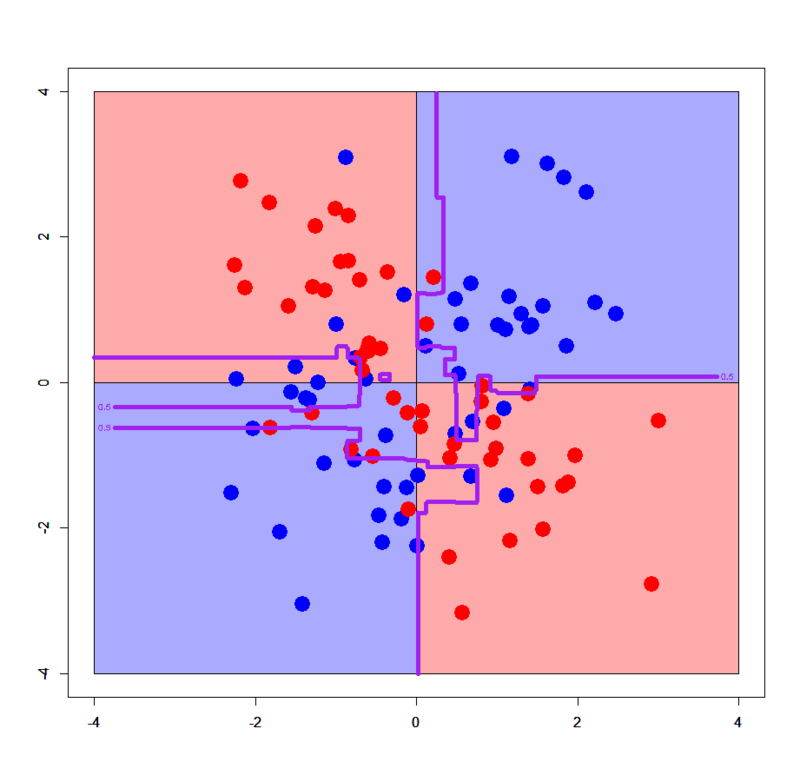
etaの値を変えることでオーバーフィッティングしたり、逆に汎化を強めることもできることが見て取れますね。今回のXORデータは次元数もサンプルサイズも小さいので他はいじっていませんが、もちろんsubsampleやcolsample_bytreeなどを調整することでより巧みにチューニングすることができます。
決定境界を描いてみる:線形分離可能パターン
実は英語ブログでは線形分離可能パターンでも決定境界を描くというのをやっているので、こちらでもやってみましょう。GitHubリポジトリから2クラスパターン、3クラスパターンをDLしてきて以下のようにインポートしてください。
# 線形分離可能パターン > dbi<-read.table("linear_bi.txt",header=T) > dml<-read.table("linear_multi.txt",header=T) # グリッドを作る > px2<-seq(-0.5,4.5,0.03) > py2<-seq(-0.5,4.5,0.03) > pgrid2<-expand.grid(px2,py2) > names(pgrid2)<-names(dbi)[-3] # sparse.model.matrix形式に直す > dbi.mx<-sparse.model.matrix(label~.,dbi) > dml.mx<-sparse.model.matrix(label~.,dml) > pgrid2.mx<-sparse.model.matrix(~.,pgrid2) # xgb.DMatrix形式に直す > ddbi<-xgb.DMatrix(dbi.mx,label=dbi$label) > ddml<-xgb.DMatrix(dml.mx,label=dml$label) > dpgrid2<-xgb.DMatrix(pgrid2.mx) # xgb.train関数で学習モデルを推定する > dbi.gbdt<-xgb.train(params=list(objective="binary:logistic",eval_metric="logloss"),data=ddbi,nrounds=100) > dml.gbdt<-xgb.train(params=list(objective="multi:softmax",num_class=3,eval_metric="mlogloss"),data=ddml,nrounds=100) # 多クラスの場合はobjectiveとnum_classの指定に注意 # 2クラスパターン > plot(c(),type='n',xlim=c(-0.5,3.5),ylim=c(-0.5,3.5)) > par(new=T) > polygon(c(-0.5,-0.5,3.5),c(3.5,-0.5,-0.5),col='#aaaaff') > par(new=T) > polygon(c(-0.5,3.5,3.5),c(3.5,-0.5,3.5),col='#ffaaaa') > par(new=T) > plot(dbi[,-3],pch=19,col=c(rep('blue',25),rep('red',25)),cex=3,xlim=c(-0.5,3.5),ylim=c(-0.5,3.5)) > par(new=T) > contour(px2,py2,array(predict(dbi.gbdt,newdata=dpgrid2),dim = c(length(px2),length(py2))),xlim=c(-0.5,3.5),ylim=c(-0.5,3.5),lwd=6,col='purple',levels = 0.5,drawlabels = T) # 3クラスパターン > plot(c(),type='n',xlim=c(-0.5,4.5),ylim=c(-0.5,4.5)) > par(new=T) > polygon(c(-0.5,-0.5,3.5),c(3.5,-0.5,-0.5),col='#aaaaff') > par(new=T) > polygon(c(-0.5,3.5,4.5,4.5,1.0,-0.5),c(3.5,-0.5,-0.5,1.0,4.5,4.5),col='#ffaaaa') > par(new=T) > polygon(c(1.0,4.5,4.5),c(4.5,1.0,4.5),col='#ccffcc') > par(new=T) > plot(dml[,-3],pch=19,col=c(rep('blue',25),rep('red',25),rep('green',25)),cex=3,xlim=c(-0.5,4.5),ylim=c(-0.5,4.5)) > par(new=T) > contour(px2,py2,array(predict(dml.gbdt,newdata=dpgrid2),dim=c(length(px2),length(py2))),xlim=c(-0.5,4.5),ylim=c(-0.5,4.5),col="purple",lwd=6,drawlabels=T,levels=c(0.5,1.5))
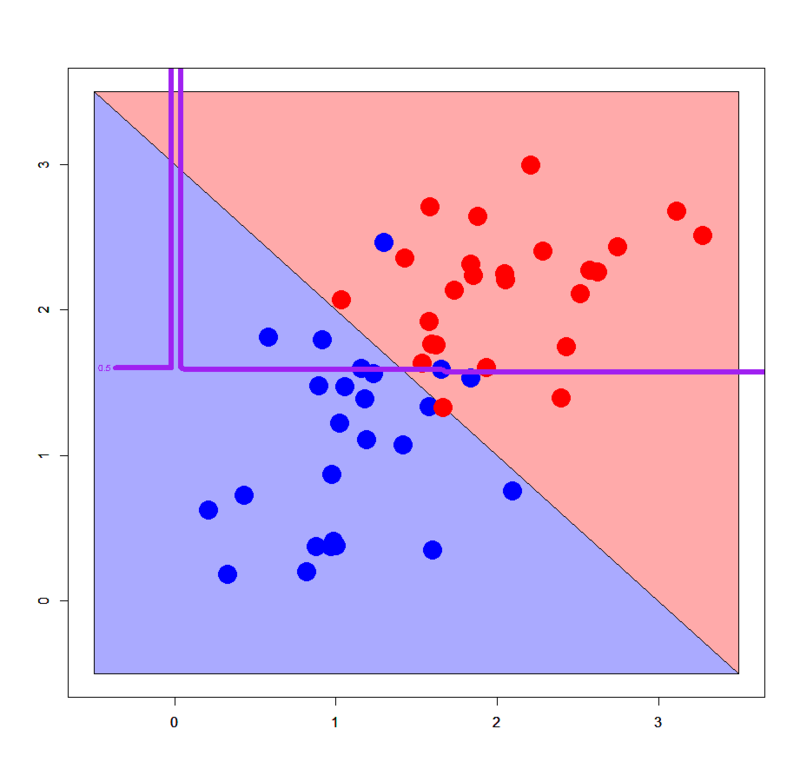
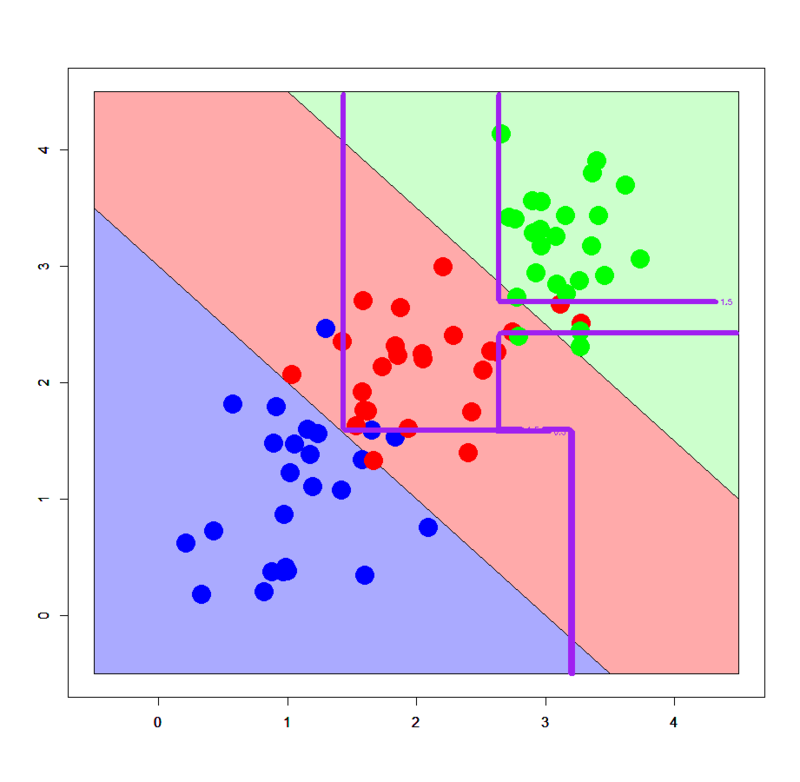
アヒャヒャヒャヒャ、全然分類できてないorz ってかこの線形分離可能パターンに対する決定境界のダメさ加減は完全に決定木のそれを踏襲してる感じですね。。。ということで、いかなXgboostといえども典型的な線形分離可能パターンに対してはうまく機能しないみたいです。
まとめ
- Xgboostはチューニング次第でDeep Learningに迫る高精度を、しかも割と低いチューニングコスト*8で実現できる
- ただし根底にあるのは樹木モデルなので、例えば決定木などと同じような振る舞いを示すことが多いっぽい
- なので線形分離不可能パターンに対しては極めて強力な一方で、線形分離可能パターンに対してはうまく機能しない可能性が高い
ってところでしょうか。色々な意味で興味深い分類器だと感じるので、今後も折に触れその挙動を試しながら理解を深めていこうかなと思ってます。