これは前回の記事の補足です。
もう見たまんまで「そもそも1クラスSVMの決定境界を具体的に描画してみたらどうなるんだろう?」という興味を持ったので、漫然と2次元でやってみます。前回の記事同様、1クラスSVMの推定に用いるのは{e1071}パッケージのsvm関数で、type = 'one-classification'と指定した場合。カーネルはガウシアンです。
なお{e1071}のvignetteにも書かれていますが、1クラスSVM (-SVM)の主問題をおさらいすると以下の通りです。
を大きく(小さく)することで、
の動ける範囲が狭く(広く)なることが見て取れます。一般に
の値は学習データそのものに分類器を適用した場合の陰性率に近くなるらしいので、例えば0.01とかにすると陰性率が1%、逆に0.99とかにすると大半が陰性ということになるようです。
適当にデータセットを作る
> set.seed(101) > tmp1 <- rnorm(1000,0,1) > set.seed(102) > tmp2 <- rnorm(1000,0,1) > d <- data.frame(x=tmp1, y=tmp2) > plot(d, pch=19, cex=0.5, xlim=c(-4,4), ylim=c(-4,4))
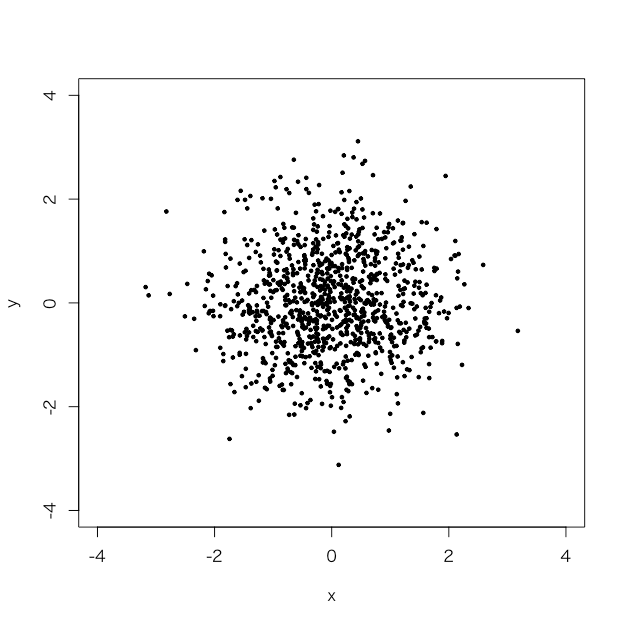
完全に適当です。
tune.svmで定めたパラメータに基づいてやってみる
> library(e1071) > tuned <- tune.svm(x=d, y=rep(TRUE, nrow(d)), type='one-classification', kernel='radial', gamma=1e-3:1, nu=1e-2:1) > tuned$best.parameters gamma nu 1 0.001 0.01 > d.svm <- svm(x=d, y=NULL, type='one-classification', kernel='radial', gamma=tuned$best.parameters$gamma, nu=tuned$best.parameters$nu) > px <- seq(-4,4,0.05) > py <- seq(-4,4,0.05) > pgrid <- expand.grid(px,py) > names(pgrid) <- names(d) > pred <- predict(d.svm, newdata=pgrid) > pred.num <- as.integer(pred) > plot(d, pch=19, cex=0.5, xlim=c(-4,4), ylim=c(-4,4), xlab='', ylab='') > par(new=T) > contour(px, py, array(pred.num, dim=c(length(px),length(py))), levels=0.5, labels = '', xlim=c(-4,4), ylim=c(-4,4), lwd=5, col='red')
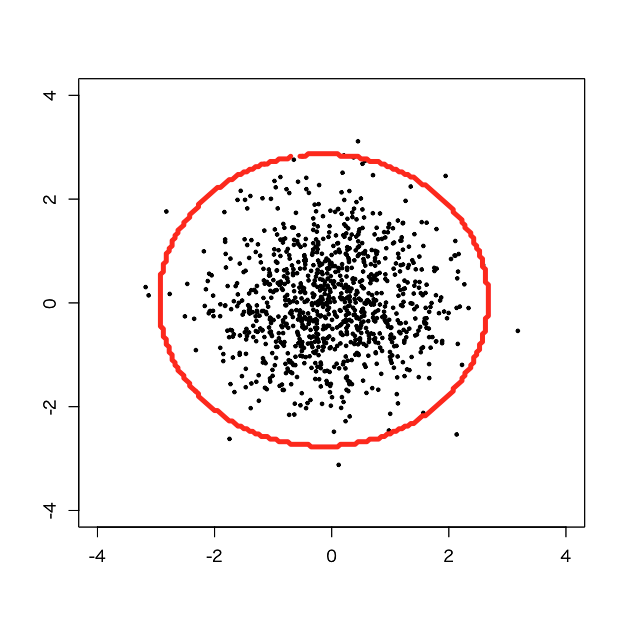
いい感じに見えますが、多少学習データそのものにも異常値と判定されているサンプルが目につきますね。
適当に手でいじってみる
上記の決定境界に対して、パラメータを変えるとどのような影響が出るかを見てみます。まず、nuを10で割ってみます。が大きい側まで許容されるようになるはずです。
> d.svm <- svm(x=d, y=NULL, type='one-classification', kernel='radial', gamma=tuned$best.parameters$gamma, nu=tuned$best.parameters$nu/10) > pred <- predict(d.svm, newdata=pgrid) > pred.num <- as.integer(pred) > plot(d, pch=19, cex=0.5, xlim=c(-4,4), ylim=c(-4,4), xlab='', ylab='') > par(new=T) > contour(px, py, array(pred.num, dim=c(length(px),length(py))), levels=0.5, labels = '', xlim=c(-4,4), ylim=c(-4,4), lwd=5, col='red')
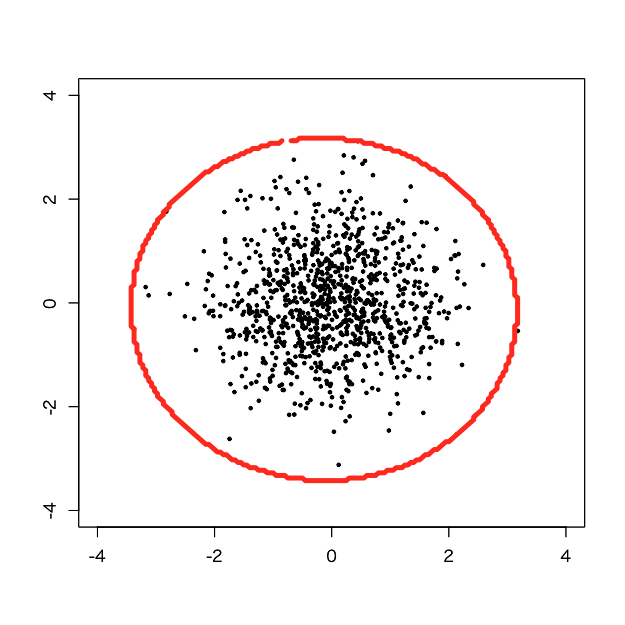
1つのサンプルを除き、全てのサンプルが決定境界内に収まりました。
今度は逆に1 - nuしてみましょう。
> d.svm <- svm(x=d, y=NULL, type='one-classification', kernel='radial', gamma=tuned$best.parameters$gamma, nu=1-tuned$best.parameters$nu) > pred <- predict(d.svm, newdata=pgrid) > pred.num <- as.integer(pred) > plot(d, pch=19, cex=0.5, xlim=c(-4,4), ylim=c(-4,4), xlab='', ylab='') > par(new=T) > contour(px, py, array(pred.num, dim=c(length(px),length(py))), levels=0.5, labels = '', xlim=c(-4,4), ylim=c(-4,4), lwd=5, col='red')
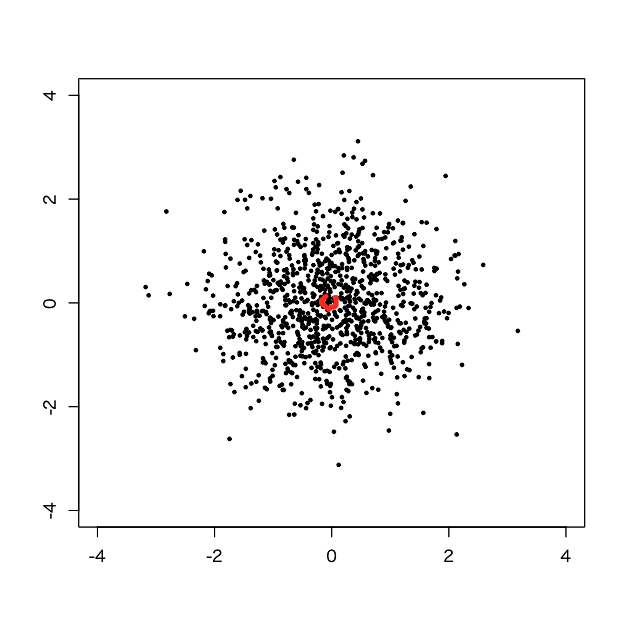
あひゃひゃ、ほぼ全てが異常値になってしまいました(汗)。やはりnuは小さくないとダメみたいですね。
念のため、nuを100で割った値にしてみます。
> d.svm <- svm(x=d, y=NULL, type='one-classification', kernel='radial', gamma=tuned$best.parameters$gamma, nu=tuned$best.parameters$nu/100) > pred <- predict(d.svm, newdata=pgrid) > pred.num <- as.integer(pred) > plot(d, pch=19, cex=0.5, xlim=c(-4,4), ylim=c(-4,4), xlab='', ylab='') > par(new=T) > contour(px, py, array(pred.num, dim=c(length(px),length(py))), levels=0.5, labels = '', xlim=c(-4,4), ylim=c(-4,4), lwd=5, col='red')
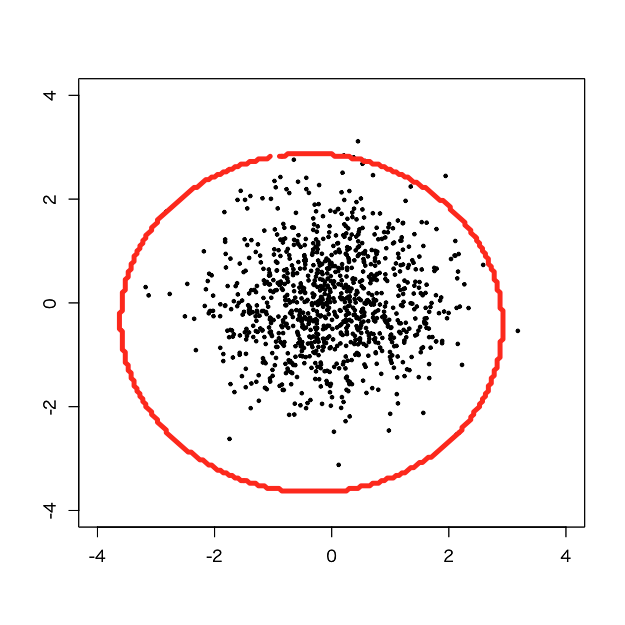
あれれ、中心からずれた挙句学習データの陰性率が上がってしまった気がします。。。
今度はnuをbest parameterを10で割った値(上記のようにほぼ全てのサンプルが陽性になる)に固定して、カーネル側をいじってみましょう。まず、gammaを1000倍してみます。過学習気味になるはずです。
> d.svm <- svm(x=d, y=NULL, type='one-classification', kernel='radial', gamma=tuned$best.parameters$gamma*1000, nu=tuned$best.parameters$nu/10) > pred <- predict(d.svm, newdata=pgrid) > pred.num <- as.integer(pred) > plot(d, pch=19, cex=0.5, xlim=c(-4,4), ylim=c(-4,4), xlab='', ylab='') > par(new=T) > contour(px, py, array(pred.num, dim=c(length(px),length(py))), levels=0.5, labels = '', xlim=c(-4,4), ylim=c(-4,4), lwd=5, col='red')
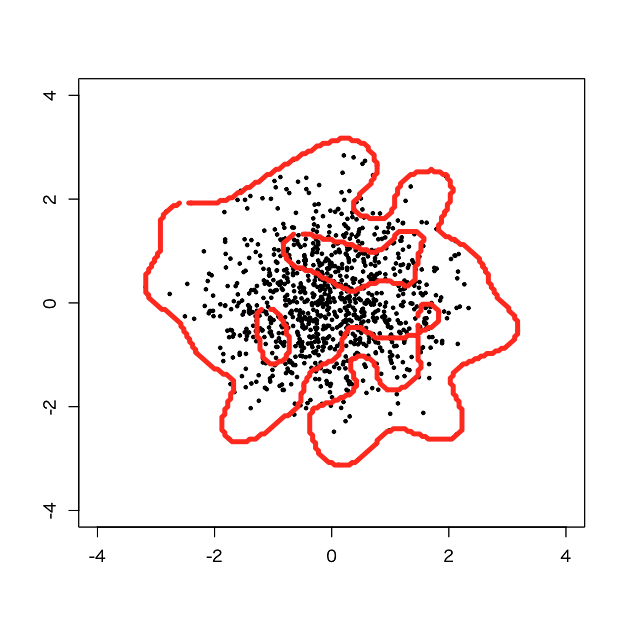
うあー、気持ち悪い決定境界になりました(笑)。真ん中に大穴がいくつも空いて、変てこな陰性判定になってしまっています。
今度は、gammaを10000で割ってみます。逆に汎化が強くなるはずです。
> d.svm <- svm(x=d, y=NULL, type='one-classification', kernel='radial', gamma=tuned$best.parameters$gamma/10000, nu=tuned$best.parameters$nu/10) > pred <- predict(d.svm, newdata=pgrid) > pred.num <- as.integer(pred) > plot(d, pch=19, cex=0.5, xlim=c(-4,4), ylim=c(-4,4), xlab='', ylab='') > par(new=T) > contour(px, py, array(pred.num, dim=c(length(px),length(py))), levels=0.5, labels = '', xlim=c(-4,4), ylim=c(-4,4), lwd=5, col='red')
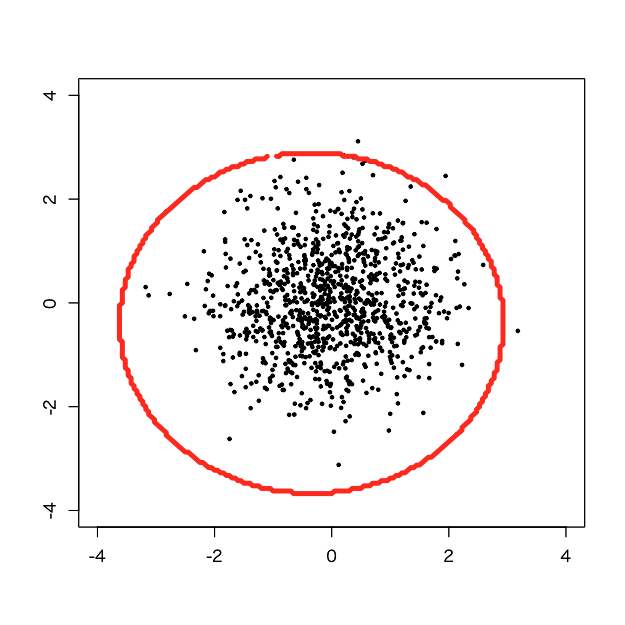
おや?これはnuを100で割った時と同じ決定境界に見えます。ということは、もしかしたら。。。
そこで、gammaとnuをで割った値同士にしてみます。
> d.svm <- svm(x=d, y=NULL, type='one-classification', kernel='radial', gamma=tuned$best.parameters$gamma/sqrt(10), nu=tuned$best.parameters$nu/sqrt(10)) > pred <- predict(d.svm, newdata=pgrid) > pred.num <- as.integer(pred) > plot(d, pch=19, cex=0.5, xlim=c(-4,4), ylim=c(-4,4), xlab='', ylab='') > par(new=T) > contour(px, py, array(pred.num, dim=c(length(px),length(py))), levels=0.5, labels = '', xlim=c(-4,4), ylim=c(-4,4), lwd=5, col='red')
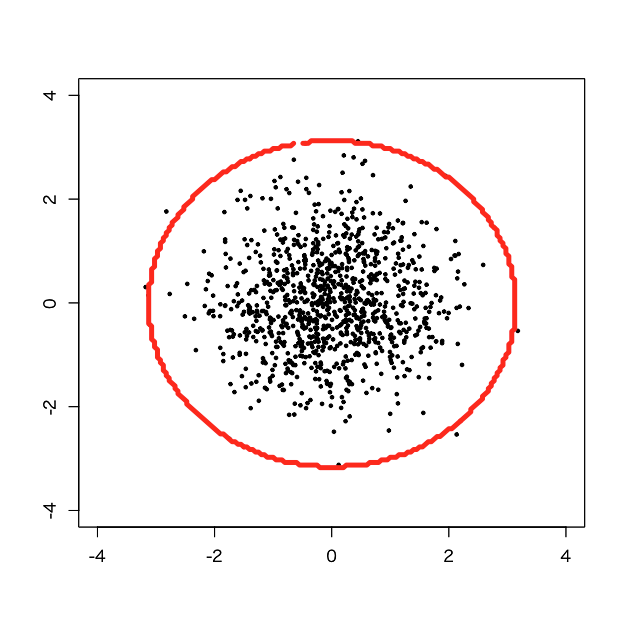
ぴったり一緒とまでは言いませんが、nuを10で割った時とよく似た結果になりました。もしかしたら、gammaとnuとの間には何かしらのトレードオフ的な関係が(主問題の式からは僕はピンと来ないのですが)あるのかもしれません。
と、いう感じの適当な実験記録でした。