Rで計量時系列分析：VARモデルから個々の時系列データ間の因果関係を推定する

前回の記事ではVARモデルの基礎までを取り上げました。ということで、今回はVARモデルに基づいて異なる時系列同士の因果関係を推定する3つの手法について取り上げてみようと思います。

ということで毎回毎回しつこいですが、使用テキストはいつもの沖本本です。

経済・ファイナンスデータの計量時系列分析 (統計ライブラリー)

作者:竜義, 沖本
朝倉書店

Amazon

以下タイトルにのっとってRで各モデルの挙動を見ながらやっていきます。

必要なRパッケージ＆サンプルデータ

{vars}をインストールして展開して下さい。なお、Granger因果のグラフ構造表現及び偏Granger因果は、実はそもそもRでは実装されていません。ここだけMatlabの話題になりますので、悪しからずご了承を。。。

それから今回のサンプルデータですが、また{vars}同梱のCanadaでは芸がないので違うデータを使うことにします。沖本先生のwebサイトに沖本本の第4章『VARモデル』章末演習で使われたサンプルデータMSCI（G7各国の株式収益率）のExcelファイルがありますので、そちらを今回は使いましょう。なお、面倒な人のためにテキストにしたものをGitHubリポジトリに置いてあります。

とりあえず、サンプルデータMSCIの日付を除いた部分をインポートしてデータフレームとして読み込みます。ここでは仮にmsciというデータフレームにしましょう。

その後は、前回の記事に従ってVARモデルを推定しておきましょう。

> VARselect(msci)
$selection
AIC(n)  HQ(n)  SC(n) FPE(n) 
     3      2      2      3 

$criteria
                  1            2            3            4            5
AIC(n) 3.062130e+01 3.018250e+01 3.012931e+01 3.014230e+01 3.015404e+01
HQ(n)  3.070064e+01 3.033127e+01 3.034750e+01 3.042992e+01 3.051108e+01
SC(n)  3.083340e+01 3.058019e+01 3.071259e+01 3.091117e+01 3.110849e+01
FPE(n) 1.989120e+13 1.282615e+13 1.216191e+13 1.232124e+13 1.246715e+13
                  6            7            8            9           10
AIC(n) 3.016358e+01 3.018662e+01 3.020425e+01 3.023091e+01 3.025758e+01
HQ(n)  3.059005e+01 3.068251e+01 3.076956e+01 3.086565e+01 3.096174e+01
SC(n)  3.130363e+01 3.151225e+01 3.171547e+01 3.192772e+01 3.213998e+01
FPE(n) 1.258751e+13 1.288187e+13 1.311235e+13 1.346856e+13 1.383493e+13

> msci.var<-VAR(msci,p=3)

以下このmsci.var (varest[10])をベースにして、Rで実際の分析手順を見ていくことにします。

因果関係の推定とは

VARモデルを用いる最大の利点として、「異なる時系列データ同士のダイナミックな関係性を推定できる」ということがあります。というより、これをやらないのであればVARモデルを当てはめる理由はない、ぐらいの重要なポイントです。

例えば、テレビCMを○月×日から△月□日まで打ったんだけれども、それはどれくらい看板商品の売上高に影響したのか？　はたまた重なる時期に雑誌広告も集中して打ったけど、それとの関係はどうなのか？　というようなことが知りたい時に、広告の出稿量を定量的な時系列データとして使えるのであればそれが売上高とどう関連しているかをVARモデルに基づいて示すことができる、という按配です。

他にも、時系列として得られる何らかのマクロな集計データ（プラットフォーム内の総課金UU数とか総DAUに対する課金UU率とか）同士が、どのように影響し合っているかについても、時間的なばらつきを考慮した上で推定することもできます。個人的には、全数データではカバーしきれず不確定要因が多い数値同士の関係性を見る際には、かなり威力を発揮するのではないか？と思ってます。

ということで、その方法論を見ていきましょう。

インパルス応答推定

沖本本と順番が違いますがこれには理由があって、この手法は次回の記事で述べる「見せかけの回帰」の影響に左右されないからです*1。

そのコンセプトとしては、「ある時系列データに何かしらの変動があった時にそれが他の時系列データにどう伝わっていくかを（時間遅れまで含めて）モデリングする」というもの。制御工学で言えば伝達関数そのものですね*2。

で、沖本本の記述なんですがirf(){vars}関数ではデフォルトになってない非直交化インパルス応答関数の話をまずしていて、それからデフォルトで使われている直交化インパルス応答関数の話をしています。ここでは冗長になるのを避けるため、後者の直交化インパルス応答関数だけを取り上げます。

インパルス応答関数の基本的なアイデアを知るために、沖本本p.84に書かれている非直交化インパルス応答関数の定義と、p.87に書かれている直交化インパルス応答関数の定義を引用しておきます。

まず、VARモデルの定義式を眺めてみましょう。

$\mathbf{y_t}=\mathbf{c}+\mathbf{\Phi_1}\mathbf{y_{t-1}}+\cdots+\mathbf{\Phi_p}\mathbf{y_{t-p}}+\mathbf{\epsilon_t}, \mathbf{\epsilon_t} \sim W.N.(\mathbf{\Sigma})$
（ただし $\mathbf{c}$ は $n \times 1$ 定数ベクトル、 $\mathbf{\Phi_i}$ は $n \times n$ 係数行列）

ここで $\mathbf{\Sigma}$ は対角行列ではないとします。この時、インパルス応答関数は以下のように定義されます。

定義4.3（非直交化インパルス応答関数） $y_{jt}$ の撹乱項 $\epsilon_{jt}$ だけに1単位（または1標準偏差）のショックを与えたときの $y_{i,t+k}$ の変化は、 $y_j$ のショックに対する $y_i$ のk期後の非直交化インパルス応答と呼ばれる。また、それをkの関数としてみたものは、 $y_j$ のショックに対する $y_i$ の非直交化インパルス応答関数といわれる。

定義4.4（直交化インパルス応答関数）撹乱項の分散共分散行列の三角分解を用いて、撹乱項を互いに相関する部分と無相関な部分に分解したとき、無相関な部分は直交化撹乱項といわれる。また、 $y_j$ の直交化撹乱項に1単位または1標準偏差のショックを与えたときの $y_i$ の直交化インパルス応答を時間の関数としてみたものは、 $y_j$ に対する $y_i$ の直交化インパルス応答関数といわれる。

理論的な定義を全部書いていくと死んでしまうので*3、要点だけ抜粋しておきます。Rで主に用いることになる直交化インパルス応答関数を求める際に重要になるのは、撹乱項 $\mathbf{\epsilon}_t$ の分散共分散行列 $\mathbf{\Sigma}$ です。この $\mathbf{\Sigma}$ は、

$\mathbf{\Sigma} = \mathbf{ADA'}$
（ただし $\mathbf{A}$ は対角成分が1に等しい下三角行列、 $\mathbf{D}$ は対角行列）

と三角分解することができ、このとき直交化撹乱項 $\mathbf{u}_t$ を

$\mathbf{u}_t = \mathbf{A}^{-1} \epsilon_t$

と定義し、各変数固有の変動を表すとみなすことができます。なお、 $\mathbf{u}_t$ は互いに無相関です（ただし $Var(\mathbf{u}_t)=\mathbf{D}$ ：証明は沖本本を参照のこと）。

$y_j$ のショックに対する $y_i$ のインパルス応答関数は、 $u_{jt}$ に1単位のショックを与えたときの $y_i$ の反応を時間の関数として見たものであり、

$IRF_{ij}(k) = \frac{\partial y_{i,t+k}}{\partial u_{jt}}$
$k = 0,1,2,\cdots$

と表されます。1単位ではなく1標準偏差のショックを与えたいときは、上の式にそのまま $\sqrt{Var(u_{jt})}$ を乗じれば良いだけです。

なのですが、Rでは三角分解の代わりにコレスキー分解を用いて撹乱項を分解し、その分解した撹乱項に1単位のショックを与えてインパルス応答関数を計算するという方法を用いています。これについてちょっと書いておきましょう。 $\mathbf{D}^{1/2}$ を(j,j)成分が $u_{jt}$ の標準偏差に等しい対角行列であるとすると、

$\mathbf{\Sigma} = \mathbf{ADA'}$

は、 $\mathbf{P} \equiv \mathbf{AD}^{1/2}$ として

$\mathbf{\Sigma} = \mathbf{AD}^{1/2} \mathbf{D}^{1/2} \mathbf{A'} = \mathbf{PP'}$

と書けます。この式は正定値行列 $\mathbf{\Sigma}$ のコレスキー分解になっていて、 $\mathbf{P}$ はコレスキー因子と呼ばれます。この $\mathbf{P}$ を用いれば、撹乱項を

$\mathbf{v}_t = \mathbf{P}^{-1}\mathbf{\epsilon}_t = \mathbf{D}^{-1/2}\mathbf{A}^{-1}\mathbf{\epsilon}_t = \mathbf{D}^{-1/2}\mathbf{u}_t$

と分解することもできます。なお $Var(\mathbf{u}_t)=\mathbf{D}$ であることから、 $v_{jt}$ は $u_{jt}$ をその標準偏差 $\sqrt{Var(u_{jt})}$ で割ったものになっています。これは言い換えると $v_{jt}$ における1単位の増加が $u_{jt}$ における1標準偏差の増加に等しいということであり、同じ要領で言えば $v_{jt}$ に1単位のショックを与えて計算したインパルス応答関数は、 $u_{jt}$ に1標準偏差のショックを与えて計算したインパルス応答関数に等しくなるということです。

一般には1標準偏差あたりのショックを用いることが多いことから、Rはじめ多くの統計分析ツールではコレスキー分解が使われているのだろう、とは沖本先生のコメントです。

追記（2022年7月20日）
事のついでがあって調べていたら、「ショックの大きさ」を求める方法の解説がされた記事を見つけました。同じ疑問を持っている方のお役に立つかと思いますので、古い記事ですがこちらに追記の形で紹介させていただきます。

さて、具体的にどういう計算をするかは沖本本pp.88-90をお読み頂くとして、実際にRでどうやるかを見ていきましょう。これは猛烈に簡単です。irf(){vars}関数でサクッと求めることができます。

> msci.irf<-irf(msci.var,n.ahead=14,ci=0.95)
# 14期先までインパルス応答関数を計算
# 信頼区間はブートストラップ法で算出される
> plot(msci.irf)

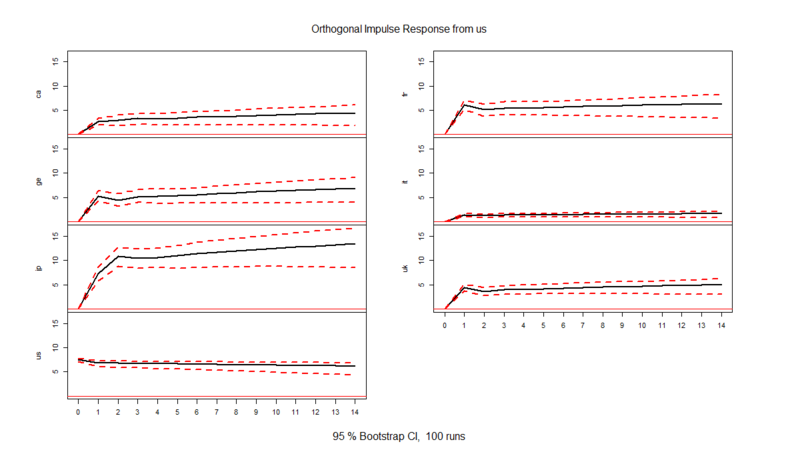
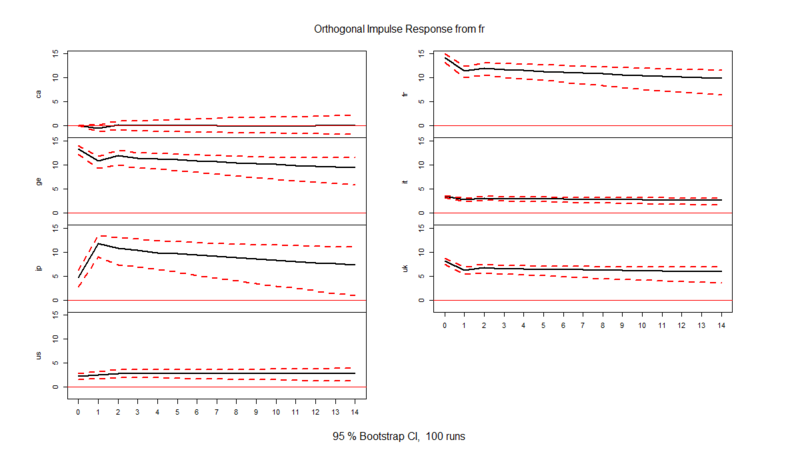
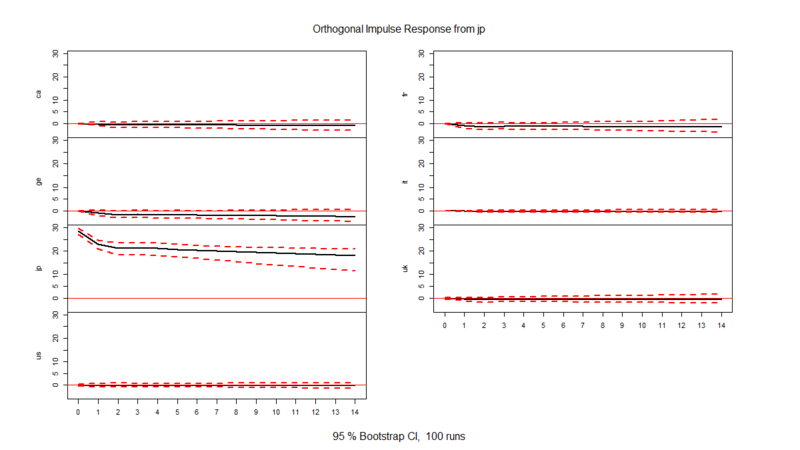
上からアメリカ、フランス、日本の順に、1標準偏差のショックを与えた時のインパルス応答関数を並べてあります。見方としては、信号処理工学の世界で言われるインパルス応答の解釈と同じで*4「ある国のMSCIにインパルス入力をぶち込んだ時にどれくらいの時間遅れレスポンスが他の国のMSCIに見られるか」が、この図から分かるという感じです。

まぁもう見たまんまで、アメリカの影響でけー、フランスも結構強いー、日本弱ぇーってところでしょうか（笑）。沖本本では市場のタイムゾーンの影響がかなり強く指摘されていますが、一方で多国間での経済依存度もかなり影響しているように読み取れる気がします。

大事なのは、「時間遅れ（タイムラグ）」の向き。ここを見ることで、「どの時系列がどの別の時系列に対して影響を与える＝どちらが原因でどちらが結果か」が分かります。

あまり計量経済学では使わないんだろうなと思いますが、理論上はこのインパルス応答関数を特定の時系列データに重畳することで、別の時系列データの予測値を出すこともできるはずです。特に冒頭で例に挙げたようなテレビCM効果などのように、予めどのくらいCMを打つかが事前に計画されているようなケースでは有効だと個人的には考えています。

Granger因果 / 偏Granger因果

因果関係を求めるというと、こちらの方が主流でしょう。2003年のノーベル経済学賞に輝いたSir Clive W. J. Granger（2009年逝去）が提唱した「時系列間の因果関係」の概念に基づき、ズバリ時系列データ同士の因果関係を推定する手法です。

沖本本pp.79-84にも書かれている通り、Grangerがこの方法論を提唱した動機はものすごくシンプルです。要は「時系列分析のアドバンテージは『背後に明確な理論がなくてもデータドリブンでいけちゃう』ということなので、データだけから因果性の有無を判断できる概念があったら楽なんじゃね？」ということ。そこで、何の理論にも基づかない予測を基準とする因果性の概念をGrangerは提案したわけです。その定義は沖本本p.80にもある通り。

定義4.1（グレンジャー因果性）現在と過去の $x$ の値だけに基づいた将来の $x$ の予測と、現在と過去の $x$ と $y$ の値に基づいた将来の $x$ の予測を比較して、後者のMSEの方が小さくなる場合、 $y_t$ から $x_t$ へのグレンジャー因果性(Granger causality)が存在するといわれる。

定義4.2（一般的なグレンジャー因果性） $\mathbf{x}_t$ と $\mathbf{y}_t$ をベクトル過程とする。また、 $x$ と $y$ の現在と過去の値を含む、時点 $t$ において利用可能な情報の集合を $\Omega_t$ とし、 $\Omega_t$ から現在と過去の $\mathbf{y}$ を取り除いたものを $\tilde{\Omega}$ とする。このとき、 $\tilde{\Omega}_t$ に基づいた将来の $\mathbf{x}$ の予測と、 $\Omega_t$ に基づいた将来の $\mathbf{x}$ の予測を比較して、後者のMSEのほうが小さくなる場合、 $\mathbf{y}_t$ から $\mathbf{x}_t$ へのグレンジャー因果性が存在するといわれる。ここで、MSEの大小は行列の意味での大小であることに注意されたい。

コンセプトとしては「ある時系列データAの未来の変動の予測性が他の時系列データBによって改善するのであれば、B→Aという因果関係があるとみなす」ということですね。

またVARモデルの具体的な式表現をズラズラ並べるのはだるいので割愛して（笑）、原理面は沖本本pp.80-81の2変量VAR(1)モデルの例を読んでもらうとして、一足飛びにGranger因果性検定の手順を沖本本pp.81-82から以下に引用します。

n変量VAR(p)モデルにおけるグレンジャー因果性検定の手順

(1) VARモデルにおける $y_{kt}$ のモデルをOLSで推定し、その残差平方和を $SSR_1$ とする。
(2) VARモデルにおける $y_{kt}$ のモデルに制約を課したモデルをOLSで推定し、その残差平方和を $SSR_0$ とする。
(3) F統計量を
$F \equiv \frac{(SSR_0 - SSR_1)/r}{SSR_1 / (T-np-1)}$
で計算する。ここで、rはグレンジャー因果性検定に必要な制約の数である。
(4) $rF$ を $\chi^2(r)$ の95%点と比較し、 $rF$ のほうが大きければ、ある変数（群）から $y_{kt}$ へのグレンジャー因果性は存在し、小さければグレンジャー因果性は存在しないと結論する。

ということで、基本的にはこの $rF$ 要約統計量を計算することがゴールだということになります。

Rで計算するにはcausality(){vars}関数を使います。既に手元にあるmsci.varに対して、以下のように実行することで具体的にGranger因果性検定の結果が得られます。

> causality(msci.var,cause="us")
$Granger

	Granger causality H0: us do not Granger-cause ca fr ge it jp uk

data:  VAR object msci.var
F-Test = 15.9065, df1 = 18, df2 = 9562, p-value < 2.2e-16
# アメリカの株式収益率は、他の6ヶ国に対してGranger因果の意味で影響を及ぼしている


$Instant

	H0: No instantaneous causality between: us and ca fr ge it jp uk

data:  VAR object msci.var
Chi-squared = 413.9249, df = 6, p-value < 2.2e-16
# 一方でアメリカの株式収益率は有意な同時影響を他の6ヶ国に対して与えている


> causality(msci.var,cause="us",vcov.=vcovHC(msci.var))
# 不等分散性下における分散共分散行列を用いてGranger因果性検定の結果を補正する

$Granger

	Granger causality H0: us do not Granger-cause ca fr ge it jp uk

data:  VAR object msci.var
F-Test = 9.433, df1 = 18, df2 = 9562, p-value < 2.2e-16


$Instant

	H0: No instantaneous causality between: us and ca fr ge it jp uk

data:  VAR object msci.var
Chi-squared = 413.9249, df = 6, p-value < 2.2e-16


> causality(msci.var,cause="jp")
$Granger

	Granger causality H0: jp do not Granger-cause ca fr ge it uk us

data:  VAR object msci.var
F-Test = 1.5482, df1 = 18, df2 = 9562, p-value = 0.06437
# 逆に日本は他の6ヶ国に対して有意なGranger因果の意味での影響を与えていない


$Instant

	H0: No instantaneous causality between: jp and ca fr ge it uk us

data:  VAR object msci.var
Chi-squared = 49.1682, df = 6, p-value = 6.9e-09

結果は概ね沖本本pp.82-83と同じようになるはずです。ところで、Granger因果を用いる際にはいろいろな注意点があります。まず、Granger因果性は通常の因果性とは異なります（Granger因果性は通常の因果性が存在する必要条件ではあるが十分条件ではない）*5。また機械的に計算するだけで因果性を出そうとする代物なので、場合によっては実際の（背景となる経済理論・社会理論から導かれる）因果性とは逆向きになってしまうこともあります。さらに書くと、Granger因果は「向き」が分かるだけでその「強度」などは分かりません。その辺の制約条件を踏まえた上で使うべきということに注意が必要です。

そして最大の問題として、「見せかけの回帰」が生じる状況下ではGranger因果は使えず、1階階差を取った差分時系列に適用せざるを得ないというポイントがあります。これは次回の記事で述べる予定です。

ところで、Granger因果はそのままだと第三者変数からの影響を受けてしまうという考え方があり、これを偏相関のアナロジーで排除してやろうという方法論があります。その方法論を偏Granger因果*6と言って、前にいた業界では僕も研究目的で利用していました。ちなみにRではまだパッケージが出ていませんがMatlabにはGCCA toolboxというライブラリがあります*7。

このGCCA toolbox、何故かマトリクスのまま偏Granger因果を計算してグラフ構造として因果性の向きを表示することが可能です。試しにMSCIデータに対して実施してみると、こうなります（Matlabコードは煩雑なので省略）。

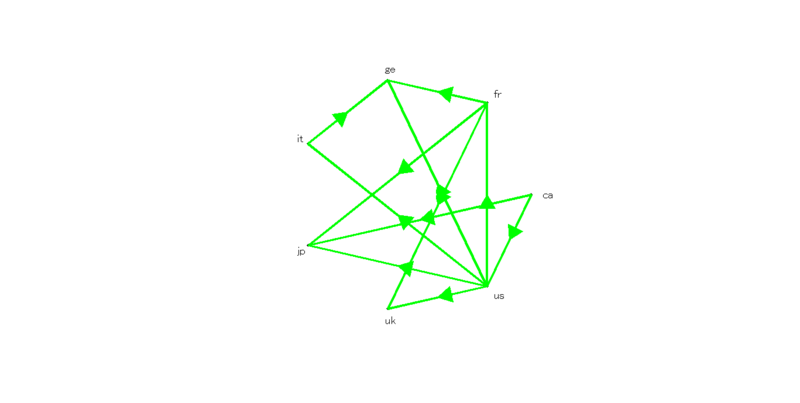
なお、偏Granger因果の $F$ 要約統計量がどの確率分布に従うかは全く分かっていないので、ブートストラップ法で有意確率を求めるしかないという問題点があります。ですが、実際に偏Granger因果を用いると微妙に結果が変わることが分かっているので、試してみる価値はあると思ってます。

予測誤差分散分解

実は僕もこれは正確には理解できてません（笑）。沖本本pp.94-97に正確な定義と解説が載っているので、そちらをお読みください。そして勉強された方は是非僕に教えてください（おい！）。

かいつまんで書くと、これは「ある時系列データの予測できない変動を説明するために、どの他の時系列データが重要かor寄与しているか」を突き止めるための手法です。これはGranger因果に似ている感じがしますが、因果関係の向きをズバリ出すというより「他の時系列からの寄与度」を出してやることで、広義の因果性を表そうというものだと僕は理解しています。

Rではfevd(){vars}関数を使います。以下のような感じです。

> msci.fevd<-fevd(msci.var,n.ahead=14) # 14期先まで評価する
> plot(msci.fevd)

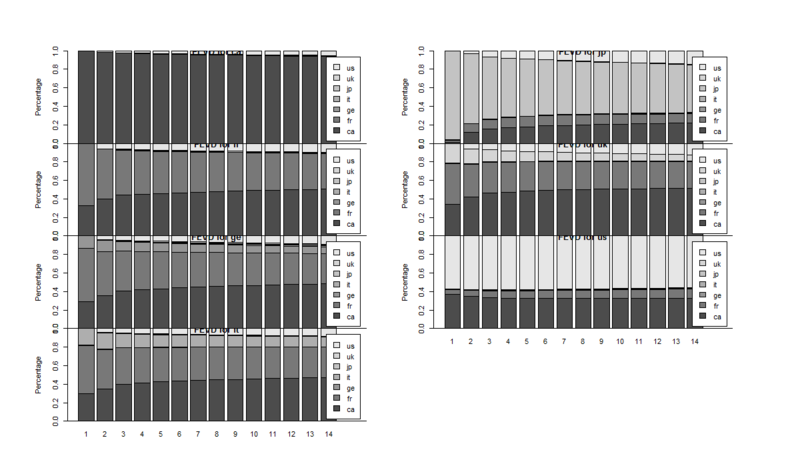
ごめんなさい、思いっ切りレイアウトが潰れてます（泣）。この図の解釈については沖本本pp.98-99の説明が参考になると思います。即ち、「プロットがどれも水平＝分散分解の結果は予測期間にほとんど依存しない＝予測そのものが難しい」「イギリス市場の変動予測についてフランス市場の寄与が大きい」みたいなことが分かる感じです。

正直言ってこれだけは未だにwebデータ分析でどう使うかまだ見出せていない状況なので、今後トライしていこうかなと思っています。。。

最後に

偏Granger因果のRパッケージはまだ地球上のどこにもないので、良かったら僕がMatlab版から移植して作ろうかなと思ってます。でもCRANパッケージを作った経験が全くないもので。。。どなたか一緒にやりませんか？

*1:こちらの資料 http://www2.e.u-tokyo.ac.jp/~seido/output/Hayashi/Hayashi_han_15.pdf によれば、たとえ見せかけの回帰がある＆共和分関係がない状況下でも、インパルス応答関数の一致性には影響がないという報告があるとのこと。出展としてこちらの論文 ftp://ftp.uic.edu/pub/depts/econ/hhstokes/e537/Sims_Stock_Watson_1990.pdf が提示されている

*2:導出の仕方が違うけど概念的にはほぼ同じ。ただし多変量の影響を均衡させているかというと微妙な気はする

*3:死ぬのは定義式全部texで書くことになる僕の方です（笑）

*4:Wikipedia英語版では信号処理工学・計量経済学それぞれの解釈がちゃんと併記されている→http://en.wikipedia.org/wiki/Impulse_response

*5:Wikipediaにも載っている例で言うと「雷が光ると雷鳴が轟くが、雷がピカッと光ること自体は雷鳴の原因ではない」

*6:定義は以下の論文を参照のこと：http://ccsb.fudan.edu.cn/ewebeditor/uploadfile/20110318163841680.pdf

*7:http://www.sussex.ac.uk/Users/anils/aks_code.htm から利用者登録すると無償でダウンロードできる

渋谷駅前で働くデータサイエンティストのブログ

元祖「六本木で働くデータサイエンティスト」です / 道玄坂→銀座→東京→六本木→渋谷駅前