Stanで統計モデリングを学ぶ(2): そもそもMCMCって何だったっけ？ - 渋谷駅前で働くデータサイエンティストのブログ

（前回記事はこちらから）

ベイジアンの知識もいい加減な僕がこんなシリーズ記事を書くとかほとんどギャグの領域なんですが（汗）*1、2回目の今回の記事ではそもそもMCMCって何だったっけ？ってところから始めようと思います。

今回参考にするのは、主に久保先生の緑本です。そもそもGLM～GLMM～階層ベイズ＋空間統計学について生態学研究をモチーフに分かりやすく書かれた本ですが、後半はMCMCの話題で統一されています。

データ解析のための統計モデリング入門――一般化線形モデル・階層ベイズモデル・MCMC (確率と情報の科学)

作者: 久保拓弥
出版社/メーカー: 岩波書店
発売日: 2012/05/19
メディア: 単行本
購入: 16人クリック: 163回
この商品を含むブログ (18件) を見る

MCMCまわりでは他にも非常に多くの良書がありますが、「初心者向けにも分かりやすくて」「段階を追って」「なぜMCMCが使えるとうれしいのか」をきちんと書いている書籍はたぶん和書では今のところこれしかないです。この記事でも基本的には緑本に沿って話を進めていきます。

端的に言うと：要は統計モデルのパラメータをモンテカルロ法で推定してくれる手法のひとつ

最近はBUGS/Stan勉強会なんかも人気を集めていて、にわかにビジネスデータ分析業界でもMCMCが注目を集めていますが、一方で業界外ではMCMCという手法そのものが何か凄いものだという印象を持っている人も結構多いと聞きます。

端的に言えば、MCMCそのものは別に凄いものでも何でもありません。これはあくまでもモンテカルロ法（いわゆる乱数シミュレーションのひとつ）の応用形で、マーケティングなり計量経済学なり生態学などの分野では統計モデルのパラメータを推定するのに利用しているというただそれだけのもの。「マルコフ連鎖モンテカルロ法」(Markov Chain Monte Carlo: MCMC)というネーミングが示しているものそのままなのです。

ところで、モンテカルロ法のイメージが浮かばないという人はこの記事をお読みの人には多分いないんじゃないかなーと思いますが*2、参考までにWikipedia記事から例を引用しておきましょう。

f:id:TJO:20140207164647g:plain:w300

（wikipedia:モンテカルロ法）

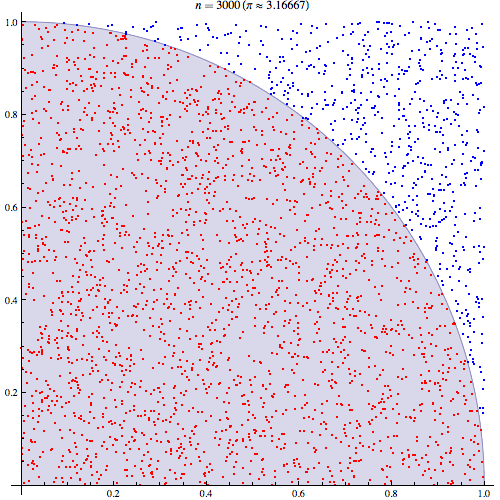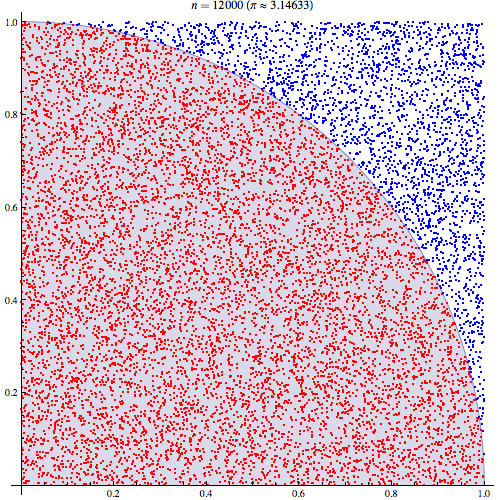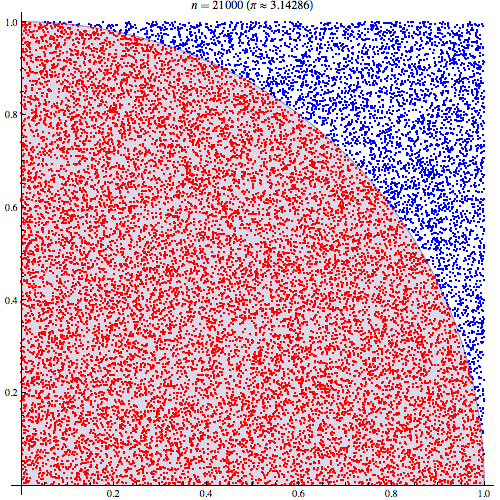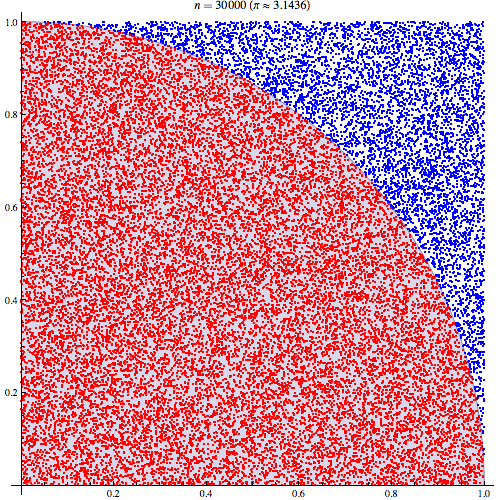
円周率πの近似計算のためにモンテカルロ法を用いた例です*3。ランダムにドットをバラバラと打っていって、90°扇形の中に入った個数をカウントすれば近似的に扇形の面積が求まるので、そこからπが求められるという按配です。

このように、適当に乱数を発生させた上で（この例ではドットを発生）、その乱数に従って何かしらの操作を行って（この例ではドットを扇形を含む正方形上に打っていく）、その結果生まれたサンプルを評価することで（この例では扇形の内側に落ちたドットをカウントする）、解析的には求まらないような何かの数値を求める（ドットのカウント数から扇形の面積を近似的に求める）、というのがモンテカルロ法の大ざっぱな説明です。

裏では何をやっているのか：「試行錯誤」でとにかくパラメータを推定しようとしている

緑本でも触れられていますが、統計モデリングにおけるパラメータ推定でMCMCを使う場合は基本的には最尤法と同じで

最尤推定量を求めるためのモデルを作り
そこから尤度が最大値を取るようにパラメータを選ぶ

だけです。ただし、単純なモデルであればパラメータで偏微分することで尤度が最大になるパラメータを選ぶのは容易ですが、関数形が複雑になればなるほど偏微分で解析的に解くのは難しくなります。そこでさらに、

パラメータをしらみつぶしに変化させて尤度を計算していく
パラメータをプラス方向かマイナス方向に変えてみて、尤度が大きくなるようならその方向に続けて変えていく
逆に尤度が小さくなるようなら、反対方向にパラメータを変えていく
このようにひとつのステップの中で前の状態に基づいて新しい状態を作りながら*4サンプリングしていく

とか*5、これを改良して

あるパラメータを除いて他のパラメータ全てを固定して
そのパラメータの事後分布をベイジアン的に発生させて新たなパラメータをサンプリングし
残りのパラメータも順次同様にベイジアン的にサンプリングし
一通りそろったところで、次のサンプリングステップを決めていく*6

みたいな方法もあります*7。どちらも1つ前の状態に基づいて次の状態への更新を行うので「マルコフ連鎖」であるとされ、それでモンテカルロ法を行っているので、「マルコフ連鎖モンテカルロ法」と呼ばれているわけです。ちなみにBUGSは後者を利用しているみたいですね*8。

これをパラメータ×尤度空間上に何となく模式図で書いてみると、こんな感じになります*9。

f:id:TJO:20140207180929p:plain

尤度の山を行ったり来たりしながら、徐々に頂上を目指していくというやり方ですね。ちなみにStanの場合はHamiltonion Monte Carlo Samplingというサンプル間の相関を低く抑えてなおかつ大域更新*10に適した手法*11と、出来るだけ元来た道を戻らないようにするサンプリング方式*12とを利用しています。

余談ですが、最後に挙げた2つは実はマルコフ連鎖に基づかないので、StanはMCMC サンプラーとは言われないんですね（笑）。モンテカルロ法であるだけになるので、MCサンプラーと称するのが正しいようです。

ということで、裏側ではとにかく乱数シミュレーションを回しているというわけです。よって手計算では無理で、計算機を回さない限り無理という。その意味では計算機が進歩した現代でこそ生きる手法と言っても良さそうです。

その意義：複雑過ぎて解析的にはパラメータが求まらないケースでもパラメータが求まる

では、何でこんな大変な思いをしてMCMCなんてやるんでしょうか？　確かに、ただの正規線形モデルなら最小二乗法で推定できますし、一般化線形モデル(GLM)ならニュートン＝ラフソン法などの数値解析的求解法が必要ながら最尤法で推定できます。個体差や場所差といった変量効果を含む一般化線形混合モデル(GLMM)でも、一応何とかならなくもないです。この辺をひとまとめにした図が、久保先生のサイトにあるのでご参考までに。

生態学データ解析 - ベイズ統計 & MCMC

しかし、さらにそれを超えた複雑なモデルになるともはや限界です。例えば2次元空間上の場所差のように変量同士でも相関があったり*13、パラメータ同士や目的変数の中に自己回帰や自己相関があるようなデータや、そもそも単一のモデル式では記述できず要素ごとに別々のモデルが介在（小売店における曜日効果・イベント効果・長期トレンド・季節成分など）した上で1つの目的変数（売上高など）を説明するような複合モデルを、最尤法でパラメータ推定しようにもモデル式が複雑過ぎてほぼほぼ不可能です*14。

そういう場合に、MCMCのような「無理やりパラメータをシミュレートして求めに行く」手法が役に立つというわけです。もちろんそれを安直だと批判する向きもないわけではありませんが、実務上は「とにかくパラメータ推定できる」ことの意義は大きいです。

特に、統数研の樋口先生も著書の中で指摘していらっしゃいますが、マーケティングデータの多くはまさにそういった「多くの要素が絡み合って簡単には解けないモデル」が根底にあるケースが多いので、今後データ分析が様々なマーケティングの現場に広まるにつれて、MCMCもまたこれまで以上*15に一般に広まっていくのかなという気がしています。

特徴：パラメータの「分布」が手に入る

基本的にやっていることは普通のモンテカルロ法と同じなので、MCMCによるサンプリング結果は「分布」として得られます。つまり、パラメータ推定をやった場合はパラメータの「分布」が手に入るわけです。前回用いたデータのパラメータ分布を{coda}パッケージを使ってプロットするとこんな感じです。

f:id:TJO:20131106124839p:plain

で、これって要は「事後分布」なんですよね。ということは、事前分布→尤度→事後分布の流れでモデル推定を行っていくベイジアンの枠組みとの親和性が高いと見ることもできます。この辺の事情については、時々このブログにもツッコミを入れて下さる@uncorrelatedさんのブログ記事が簡潔で分かりやすいかと。

ベイズ推定を知っているフリをするための知識: ニュースの社会科学的な裏側

そう、実は「事後分布」的なものを取り扱うのは決してベイジアンだけの専売特許ではないんですよね（笑）。その他のポイントについてもこちらの記事では必ずしもMCMCだから優位というわけではない旨の指摘がされています。とはいえ、複雑なモデルに対して何も考えずに突っ込めば勝手にパラメータ分布が出せるMCMCの利点は依然として大きいと言って良いのではないかと思ってます。

注意点：計算時間が長い、計算が収束しないとまずい、事前分布の選び方にコツが要るetc.

基本的に、MCMC諸手法にせよStanにせよ、要はモンテカルロシミュレーションなので計算機のパワーを食います。なので、とにかく計算時間を食います。例えば、@berobero11さんがブログ記事で紹介なさっていたサンプルケースを僕がStan 2.1.0でやってみたところ、25時間以上かかりましたorz　StanのようなC++コンパイラベースのフレームワークでこれなら、インタプリタ的なWinBUGSとかだったらどうなることやら。。。

また、計算結果のパラメータ分布が収束しなかったり、単峰性ではなく多峰性の分布になってしまうようなケースではそもそもどう解釈してよいか困ってしまいます*16。こういう場合はそもそもモデルの設定からやり直しになることもあり、そういう点ではひと手間余計にかかるともいえます。

そして、例えば潜在変数の推定みたいなケースでは無情報事前分布と階層事前分布を決める必要がありますが*17、こいつらが不適切だと結果がおかしくなることも多々あるという。これはもうケーススタディをためていって経験的に良い物を選ぶか、そういう事例の集まった資料を当たるかしかなさそうです。