Rでベイジアン動的線形モデルを学ぶ(2.5)：最尤法でパラメータ推定してみる - 渋谷駅前で働くデータサイエンティストのブログ

前回サクッとローカルレベル・モデルを推定してみたわけですが、そう言えばパラメータ推定は何もしなかったのでした。既に線形モデルも一般化線形モデルもこのブログで見てきている以上最小二乗法や最尤法やMCMCでパラメータ推定するというのは常識なわけですが、今回テキストにしているPetris本とCommandeur本の2冊とも

Rによるベイジアン動的線形モデル (統計ライブラリー)

作者: G.ペトリス,S.ペトローネ,P.カンパニョーリ,和合肇,萩原淳一郎
出版社/メーカー: 朝倉書店
発売日: 2013/05/08
メディア: 単行本
この商品を含むブログを見る

状態空間時系列分析入門

作者: J.J.F.コマンダー,S.J.クープマン,Jacques J.F. Commandeur,Sime Jan Koopman,和合肇
出版社/メーカー: シーエーピー出版
発売日: 2008/09
メディア: 単行本
購入: 2人クリック: 4回
この商品を含むブログを見る

何故か最尤法によるパラメータ推定の話題をかなり後の方に持ってきていてこのままだとそこまで到達するのに時間がかかるので*1、先にさっさと最尤法でのパラメータ推定を{dlm}でどうやってしまうのかを取り上げておくことにしておきます。

なお、今回の話題はPetris本のpp.147-150にも載っていますが、前回も沖本本の時も参考にさせていただいたLogics of Blueさんの記事も分かりやすくて良いと思うので是非是非どうぞ。

dlmMLE関数を使う

基本的にはdlmMLE関数に適当な初期値を与えてやることで最尤推定ができます。ということで、前回の記事までやったところの続きとして以下のようにやってみましょう。

> build1<-function(param){dlmModPoly(order=1,dV=exp(param[1]),dW=exp(param[2]))}
# 最尤推定したいモデルを先に関数定義の形で作っておく必要がある
# dlmModPolyで普通にランダムウォーク・プラス・ノイズモデルを指定する
# なお、基本的に対数尤度に直してから計算している都合があるので、
# パラメータは先にexpしておく必要がある。。。らしい

> fit<-dlmMLE(d2,c(1,1),build1)
# 初期値にdV=1, dW=1を入れたつもり
# build1関数を引数として与える

> d2.model2<-build1(fit$par)
# ここでは多段階最適化を行っていることになっているので、
# （※注：そうではないらしいです下記参照）
# 推定したfitの中のパラメータ部$parをbuild1関数に与えることで、
# 最尤推定値に基づくモデルd2.model2を改めて作る

> d2.filt2<-dlmFilter(d2,d2.model2)
# これをカルマンフィルタで推定する

> matplot(cbind(d2,d2.filt1$m[-1],d2.filt2$m[-1]),type='l',lwd=c(2,3,3),col=c('red','blue','purple'),lty=c(1,2,3))
# 後は前回の記事で推定したd2.filt1$mと併せてプロットするだけ

> par(mfrow=c(2,1))
> hist(d2-d2.filt1$m[-1],col='blue',main='Not MLE')
> hist(d2-d2.filt2$m[-1],col='red',main='MLE')
# 残差の分布も見てみる

f:id:TJO:20140927155406p:plain

f:id:TJO:20140927155909p:plain

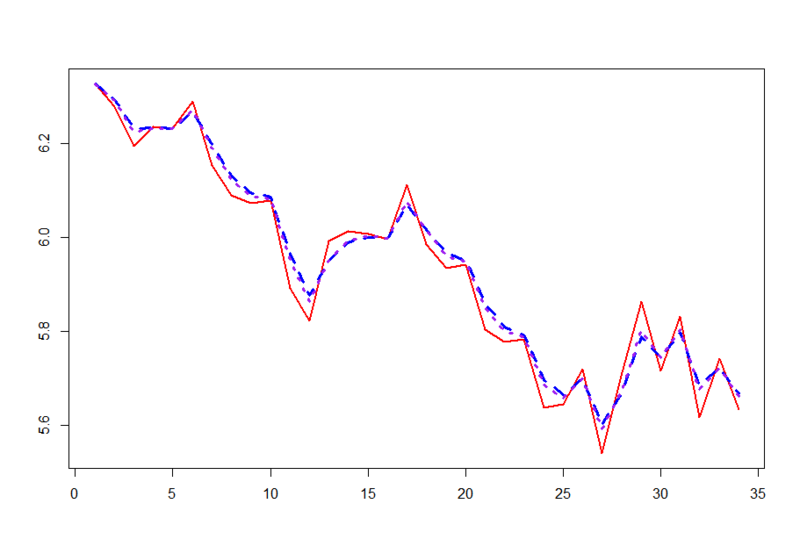
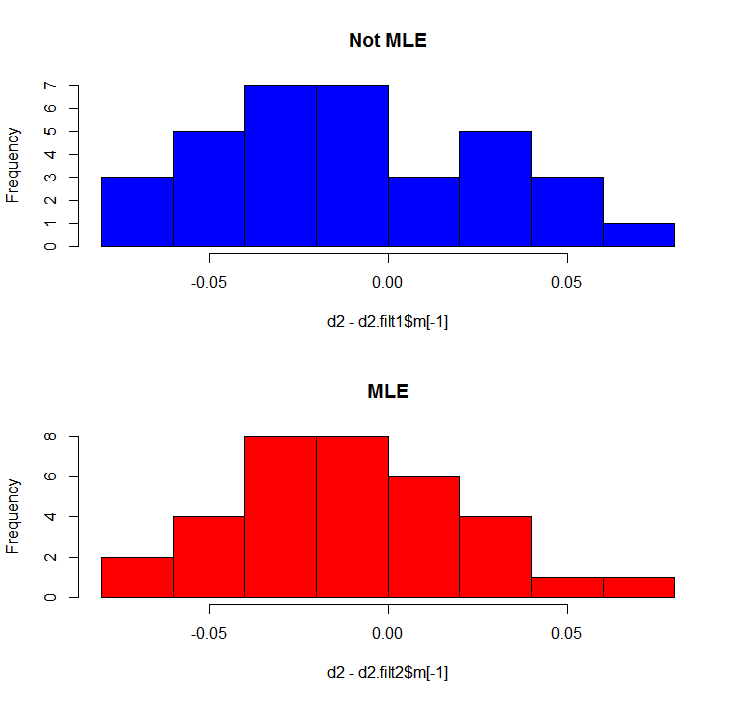
ということで、最尤法でパラメータ推定した方が残差の分布もより正規性が強くなっていることが何となく見て取れます。

注意点

Logics of Blueさんもご指摘の通りで、一般の最尤法と同じく初期値にかなり依存するケースがあるので、推定値がおかしいと思ったら毎回初期値を変えてやり直す必要があります。そのためにも、プロットなどで可視化できる場合は可視化し、できない場合でも生の推定値を目視しておかしくないかどうか確認した方が良いでしょう。

追記1

@ibaibabaibai先生から以下の如くツッコミが。

状態空間モデルで，カルマンフィルタで求めた尤度からパラメータの最尤推定をして，そのパラメータを入れてもういちどカルマンフィルタでフィルタリング・平滑化をするのは通常の意味での「多段階最適化」ではないのだよ．なぜなら，カルマンフィルタで求めた尤度は状態について周辺化した尤度だから．
— baibai (@ibaibabaibai) September 27, 2014

状態空間モデルで周辺化した尤度を使うのは極めて本質的．状態とパラメータを同時に最適化すると，手順が多段階でも１段階でも不安定になり，おそらく最大値をあたえるパラメータがゼロか無限大に飛ぶ．STANなんかで計算するいわゆるフルベイズの良い近似になっているのは周辺尤度のほう．
— baibai (@ibaibabaibai) September 27, 2014