渋谷駅前で働くデータサイエンティストのブログ

元祖「六本木で働くデータサイエンティスト」です / 道玄坂→銀座→東京→六本木→渋谷駅前

アソシエーション分析＋グラフ構造可視化 ({arules} + {arulesViz}) で教師あり学習の変数重要度を可視化する

R 機械学習 データサイエンス

グローバルTokyoRで何話そうかなー、と思っていたんですがそう言えば主賓がvisualizationの人なんだったっけなぁということで、可視化の話にでもしようかなと。ということで、僕の大好きなネタでもやろうかと思います。


それは、「とにかく{arules} + {arulsViz}で可視化してしまえ」戦略。基本的に世の中のデータマイニングにせよ分類問題にせよ、実は様々な説明変数の共起（？）関係で表せることが多く*1、そういう時は何だかんだでassociation rulesを使うのが一番手っ取り早いんですよね。僕自身の勉強不足を補う目的からも（汗）、ちょっと書いてみようと思います。


アイテム間の条件付き確率たくさん→ベイジアンネットワークもどき→有向非循環グラフ


基本的に、association rulesはアイテム間の共起確率をある状態に対する条件付き確率として出すものです*2。そしてaprioriアルゴリズムの閾値を緩めにしてある程度ルール数を沢山算出してやると、全アイテム間での条件付き確率が網羅的にたくさん出てくることになるはずです。


で、僕は完全に忘れてたんですが。これってPRML下巻第8章とか見れば分かりますが、要はベイジアンネットワーク（もどき）としても扱えるわけですよね。こいつは有向非循環グラフとしても表せるので、グラフ構造表現に置き換えることが可能です。ただしこの辺は厳密には正しくない議論で、以下の@先生とのやり取りを参照あれ。



ともあれ、ベイジアンネットワークもどきにはなるので、こいつを例えば{igraph}パッケージでグラフ構造として可視化し、さらに各種ネットワーク分析もできるというわけです。


この時、レイアウトとして描画アルゴリズムをFruchterman-Reingoldに指定します。これは力学アルゴリズムの一種で、最短経路長に応じてノード同士が近くなるようにグラフを描画するので、一般に「関連性が近いほどノード同士が近くなるように描画する」傾向があります*3。この辺は{igraph} + {arulesViz}が勝手にやってくれます。今回はそのお話がメインです。


教師あり学習のラベルもアソシエーション分析のアイテムとして置いてみると？


ここからが本題。教師あり学習のラベルを例えば[No, Yes] or [0, 1]で表しているとしましょう。これをあえて2つに分けて、noという説明変数（noのフラグが立ってる時に1 / 立ってない時に0）とyesという説明変数（yesのフラグが立ってる時に1 / 立ってない時に0）をカラムとして立てます。


そうすると、例えば他の目的変数とのかけ合わせ方とまとめて捉えることで、一種のassociation rulesとして扱うことができます。例えば、以下のようなデータを考えてみます。想定としては「とあるエンターテインメントプラットフォームで、ある月にどのソシャゲ・SNS・アプリを利用した人が翌月もプラットフォームを利用してくれるか」的なログです。


まず、オリジナルはこんな感じです（GitHubから落としてきてd1としてインポートします）。

game1 game2 game3 social1 social2 app1 app2 cv
0 0 1 1 1 1 0 Yes
0 0 1 1 0 0 0 No
1 0 1 1 1 0 0 No
1 0 0 1 0 0 1 No
1 1 1 0 1 1 0 Yes
0 1 0 1 0 0 0 No


そこで、これを以下のように直します（GitHubから落としてきてd2としてインポートします）。

game1 game2 game3 social1 social2 app1 app2 yes no
0 0 1 1 1 1 0 1 0
0 0 1 1 0 0 0 0 1
1 0 1 1 1 0 0 0 1
1 0 0 1 0 0 1 0 1
1 1 1 0 1 1 0 1 0
0 1 0 1 0 0 0 0 1


そうすると、association rulesという観点から見ると、例えば1レコード目は{game3, social1, social2, app1, Yes}というtransactionに相当することになります。このやり方で、普通に教師あり学習で分類するような問題をassociation rulesによってさばいていくということをやってみます。


Rで普通に教師あり機械学習で分けた場合と、association rulesで分けた場合とで見比べてみる


ひとまずCRANパッケージを読み込んでおきましょう。{e1071}, {randomForest}, {arules}, {arulesViz}をrequireしておきます。

> require("arules")
Loading required package: arules
Loading required package: Matrix

Attaching package: ‘arules’

The following objects are masked from ‘package:base’:

    %in%, write

> require("arulesViz")
Loading required package: arulesViz
Loading required package: scatterplot3d
Loading required package: vcd
Loading required package: grid
Loading required package: seriation
Loading required package: cluster
Loading required package: TSP
Loading required package: gclus
Loading required package: colorspace
Loading required package: igraph

Attaching package: ‘igraph’

The following object is masked from ‘package:gclus’:

    diameter


Attaching package: ‘arulesViz’

The following object is masked from ‘package:base’:

    abbreviate
> require("e1071")
Loading required package: e1071
Loading required package: class
> require("randomForest")
Loading required package: randomForest
randomForest 4.6-7
Type rfNews() to see new features/changes/bug fixes.


そしたら、まずd1に対して教師あり学習をやってみます。svm(){e1071}と、randomForest(){randomForest}と、glm(){stats}（family=binomialでロジスティック回帰）を使います。

> d1.svm<-svm(cv~.,d1)
> tuneRF(d1[,-8],d1[,8],doBest=T)
mtry = 2  OOB error = 6.2% 
Searching left ...
mtry = 1 	OOB error = 8.7% 
-0.4032258 0.05 
Searching right ...
mtry = 4 	OOB error = 6.73% 
-0.08602151 0.05 

Call:
 randomForest(x = x, y = y, mtry = res[which.min(res[, 2]), 1]) 
               Type of random forest: classification
                     Number of trees: 500
No. of variables tried at each split: 2

        OOB estimate of  error rate: 6.43%
Confusion matrix:
      No  Yes class.error
No  1400  100  0.06666667
Yes   93 1407  0.06200000
> d1.rf<-randomForest(cv~.,d1,mtry=2)
> table(d1$cv,predict(d1.svm,d1[,-8]))

        No  Yes
  No  1402   98
  Yes   80 1420

# SVMの分類結果マトリクス

> table(d1$cv,predict(d1.rf,d1[,-8]))
     
        No  Yes
  No  1413   87
  Yes   92 1408

# ランダムフォレストの分類結果マトリクス

> importance(d1.rf)
        MeanDecreaseGini
game1          20.640253
game2          12.115196
game3           2.355584
social1       189.053648
social2        76.476470
app1          796.937087
app2            2.804019

# ランダムフォレストの変数重要度

> d1.glm<-glm(cv~.,d1,family=binomial)
> summary(d1.glm)

Call:
glm(formula = cv ~ ., family = binomial, data = d1)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-3.6404  -0.2242  -0.0358   0.2162   3.1418  

Coefficients:
            Estimate Std. Error z value Pr(>|z|)    
(Intercept) -1.37793    0.25979  -5.304 1.13e-07 ***
game1        1.05846    0.17344   6.103 1.04e-09 ***
game2       -0.54914    0.16752  -3.278  0.00105 ** 
game3        0.12035    0.16803   0.716  0.47386    
social1     -3.00110    0.21653 -13.860  < 2e-16 ***
social2      1.53098    0.17349   8.824  < 2e-16 ***
app1         5.33547    0.19191  27.802  < 2e-16 ***
app2         0.07811    0.16725   0.467  0.64048    
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 4158.9  on 2999  degrees of freedom
Residual deviance: 1044.4  on 2992  degrees of freedom
AIC: 1060.4

Number of Fisher Scoring iterations: 7

# ロジスティック回帰で得られた偏回帰係数＝変数重要度


見たまんまで、翌月もプラットフォームを利用してもらうにはapp1を利用してもらうのが最も効果的で、その後social2, game1と続く感じですね。一方でsocial1, game2は非常に不評なようです。全体として見るとapp1とsocial1の変数重要度＝寄与度が非常に強い印象です。


次に、このデータのcvカラムをyesカラムとnoカラムとに分けたデータd2を用いて、apriori(){arules}関数でassociation rules analysisをやってみましょう。

> d2.ap<-apriori(as.matrix(d2))

parameter specification:
 confidence minval smax arem  aval originalSupport support minlen maxlen target   ext
        0.8    0.1    1 none FALSE            TRUE     0.1      1     10  rules FALSE

algorithmic control:
 filter tree heap memopt load sort verbose
    0.1 TRUE TRUE  FALSE TRUE    2    TRUE

apriori - find association rules with the apriori algorithm
version 4.21 (2004.05.09)        (c) 1996-2004   Christian Borgelt
set item appearances ...[0 item(s)] done [0.00s].
set transactions ...[9 item(s), 3000 transaction(s)] done [0.00s].
sorting and recoding items ... [9 item(s)] done [0.00s].
creating transaction tree ... done [0.00s].
checking subsets of size 1 2 3 4 5 done [0.00s].
writing ... [50 rule(s)] done [0.00s].
creating S4 object  ... done [0.00s].

# 50ルールしかないのでもうちょっと基準を緩める

> d2.ap<-apriori(as.matrix(d2),parameter=list(support=0.001))

parameter specification:
 confidence minval smax arem  aval originalSupport support minlen maxlen target   ext
        0.8    0.1    1 none FALSE            TRUE   0.001      1     10  rules FALSE

algorithmic control:
 filter tree heap memopt load sort verbose
    0.1 TRUE TRUE  FALSE TRUE    2    TRUE

apriori - find association rules with the apriori algorithm
version 4.21 (2004.05.09)        (c) 1996-2004   Christian Borgelt
set item appearances ...[0 item(s)] done [0.00s].
set transactions ...[9 item(s), 3000 transaction(s)] done [0.00s].
sorting and recoding items ... [9 item(s)] done [0.00s].
creating transaction tree ... done [0.00s].
checking subsets of size 1 2 3 4 5 6 7 8 done [0.00s].
writing ... [182 rule(s)] done [0.00s].
creating S4 object  ... done [0.00s].

# 182ルール得られた

> inspect(head(sort(d2.ap,by="support")))
  lhs          rhs         support confidence     lift
1 {no}      => {social1} 0.4710000  0.9420000 1.367199
2 {app1}    => {yes}     0.4636667  0.9430508 1.886102
3 {yes}     => {app1}    0.4636667  0.9273333 1.886102
4 {social2,                                           
   app1}    => {yes}     0.3190000  0.9745418 1.949084
5 {social2,                                           
   yes}     => {app1}    0.3190000  0.9327485 1.897116
6 {game1,                                             
   app1}    => {yes}     0.2826667  0.9814815 1.962963

# 上位から相関ルールを見てみた


何となく、ロジスティック回帰で見たのと同じような傾向が感じられますね。けれどもこれだけではまだよく分からない感じです。


教師あり学習データに対する相関ルールを{arulesViz}でグラフ構造として可視化してみる


そこで、既に紹介したようにこの相関ルールd2.apをグラフ構造として可視化してみましょう。やり方は非常に簡単で、{arulesViz}がrequireされていれば後は以下のようにやるだけです。

plot(d2.ap,method="graph",control=list(type="items",layout=layout.fruchterman.reingold,cex=2),margin=-0.1)
# plot.rules()メソッドを使用。control引数に{igraph}側の引数をリスト形式で入れられるようになってる


f:id:TJO:20140414112546p:plain

f:id:TJO:20140410171621p:plain


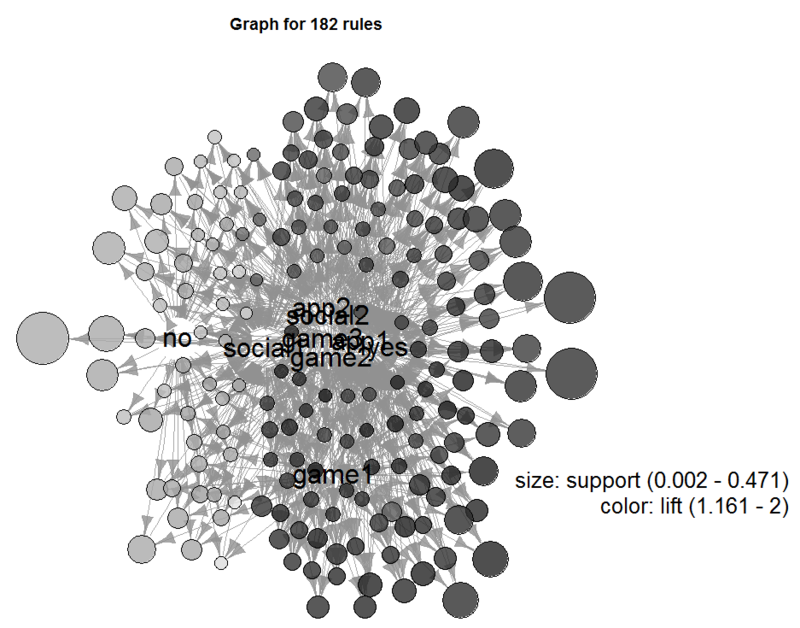
ちょっと中心の辺りにノードの字が重なり合ってしまって見づらいですが、要はyesに近ければ翌月プラットフォーム利用に効果的で、noに近ければ逆効果という判定になります。物は考えようですが、例えばyesノードとnoノードとの間に垂直二等分線を引いて、どちらに近いかで寄与度を測ることも可能です。


そうやって観察してみると、概ねロジスティック回帰とランダムフォレストで見た通りになっているのが分かるかと思います。そしてgame1が妙に浮いているのも見て取れるかと思います。このやり方だと、ただ単に機械学習の結果が何となく読み取れるだけでなく、目的変数同士の関係性も大ざっぱながら見られるというメリットがあります。


とは言え厳密なやり方ではないので過信は禁物


もう↑の通りで、これって全然厳密な話ではないので鵜呑みにすると猛烈に危険です。根底にあるロジックも単にassociation rules→ベイジアンネットワークもどき→Fruchterman - Reingoldアルゴリズムで可視化という流れをなぞっているだけなので、適当もいいところです。


とは言え、このやり方だと実は多重共線性なんかも発見しやすかったりします（目的変数ノード同士の距離から互いの相関が見て取れるので）。さらに言うと、多重共線性に引っ掛からず普通に多変量解析した正しい偏回帰係数に沿った結果になります。ということで、なかなか有用なのも事実です。


最後に


よーし、ということで今度のグローバルTokyoRはこのネタをそのままPowerPointに落として持っていって喋るだけ（笑）。余裕余裕～。

*1:猛烈に適当なことを言ってるのでツッコミはご勘弁

*2:あれ？合ってますよね？間違ってる？gkbr

*3:詳細は原論文を参照のこと→ ftp://132.180.22.143/axel/papers/reingold:graph_drawing_by_force_directed_placement.pdf