追記(2018年4月)
2017年4月にアップデート記事を出しておりますので、そちらもご覧ください。
以前の記事でSVM(しかもsvm{e1071}に限って)で不均衡データをクラス分類する方法について取り上げましたが、色々調べた結果その他のRの分類器でもやれるということが分かったので、ついでにまとめておきます。といってもSVMに加えてランダムフォレスト、ロジスティック回帰を持ってきただけですが(笑)。
なお、前回同様用いるサンプルデータは正例20個・負例600個の30倍の不均衡データです。
SVM (LIBSVM)
前回の記事で既出ですが改めて書いておきましょう。svm{e1071}ではclass.weights引数を使うことでクラス重み付けを与えることができます。マージンの重みを正例と負例とで分けるという方法論です。
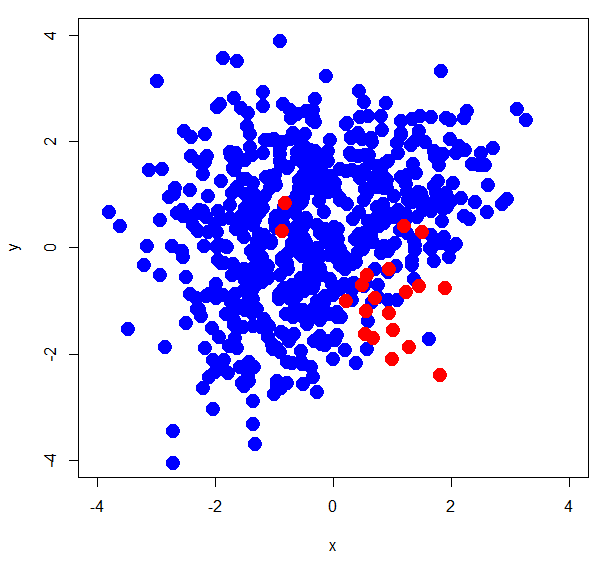
> d <- read.delim("~/xorc_ub.txt") > d$label<-as.factor(d$label) > summary(d$label) 0 1 600 20 # 正例が20個、負例が600個の不均衡データ > library(e1071) > d.svm<-svm(label~.,d) > d.svm.ub<-svm(label~.,d,class.weights=c('0'=1,'1'=30)) > out.d.svm<-predict(d.svm,newdata=pgrid) > out.d.svm.ub<-predict(d.svm.ub,newdata=pgrid) > par(mfrow=c(1,2)) > plot(d[,-3],pch=19,col=c(rep('blue',600),rep('red',20)),cex=2,xlim=c(-4,4),ylim=c(-4,4),main='Without class weights') > par(new=T) > contour(px,py,array(out.d.svm,dim=c(length(px),length(py))),xlim=c(-4,4),ylim=c(-4,4),col="purple",lwd=3,drawlabels=F) > plot(d[,-3],pch=19,col=c(rep('blue',600),rep('red',20)),cex=2,xlim=c(-4,4),ylim=c(-4,4),main='With class weights') > par(new=T) > contour(px,py,array(out.d.svm.ub,dim=c(length(px),length(py))),xlim=c(-4,4),ylim=c(-4,4),col="purple",lwd=3,drawlabels=F) > table(d$label,predict(d.svm,newdaat=d[,-3])) 0 1 0 600 0 1 19 1 > table(d$label,predict(d.svm.ub,newdaat=d[,-3])) 0 1 0 546 54 1 2 18
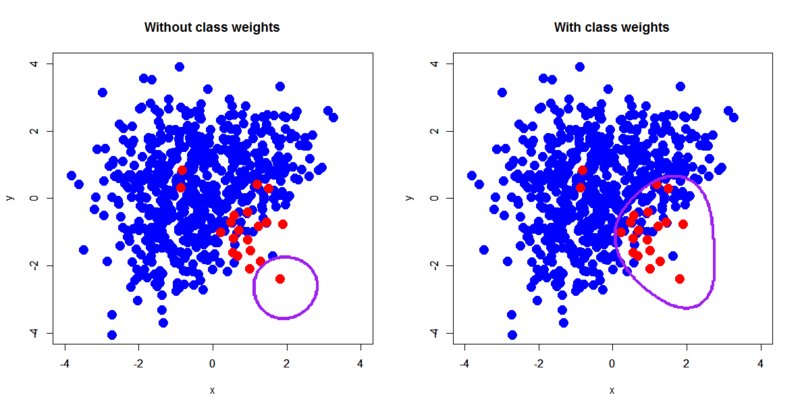
決定境界も妥当なところに落ち着いていて、confusion matrixを見ても正例の推定個数が増えています。その代わりfalse alarmも増えるというのは前回の記事で指摘した通りです。ちなみにclass.weightsの値を変化させるとこんな感じになります。
ある程度変わってる気が。。。しなくもないんですが、どうなんですかね。ここはちょっと次のランダムフォレストを見てから考えてみましょうということで。
ランダムフォレスト
randomForest{randomForest}を使う場合は、引数classwtにクラス重み付けの値をただc(1,30)といった感じでざっくり渡してやればそれでおしまいです。ちなみに以前のStackOverFlowでのこの件の問答では「未実装(何故ならウィッシュリストに入ったまんまだから)」というコメントがついていたんですが、既に実装済みだったようです。
恐らくですが、個々の木の枝分かれの際に重み付けをかけるか、最後のラベル決定の際に重み付けをかけるかのいずれかだということが@sfchaosさんのスライドから想像されますが、どちらかはヘルプを見ても不明ということで。。。
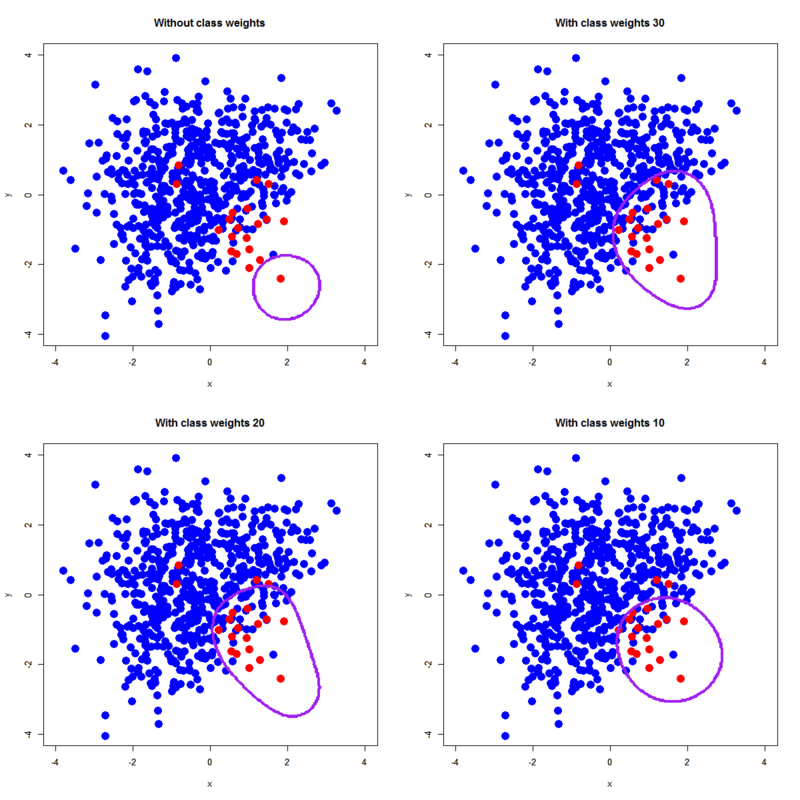
> library(randomForest) > d.rf<-randomForest(label~.,d) > d.rf.ub<-randomForest(label~.,d,classwt=c(1,30)) > px<-seq(-4,4,0.03) > py<-seq(-4,4,0.03) > pgrid<-expand.grid(px,py) > names(pgrid)<-names(d)[-3] > out.d.rf<-predict(d.rf,newdata=pgrid,type='response') > out.d.rf.ub<-predict(d.rf.ub,newdata=pgrid,type='response') > par(mfrow=c(1,2)) > plot(d[,-3],pch=19,col=c(rep('blue',600),rep('red',20)),cex=2,xlim=c(-4,4),ylim=c(-4,4),main='Without class weights') > par(new=T) > contour(px,py,array(out.d.rf,dim=c(length(px),length(py))),xlim=c(-4,4),ylim=c(-4,4),col="purple",lwd=3,drawlabels=F) > plot(d[,-3],pch=19,col=c(rep('blue',600),rep('red',20)),cex=2,xlim=c(-4,4),ylim=c(-4,4),main='With class weights') > par(new=T) > contour(px,py,array(out.d.rf.ub,dim=c(length(px),length(py))),xlim=c(-4,4),ylim=c(-4,4),col="purple",lwd=3,drawlabels=F) > table(d$label,predict(d.rf,newdata=d[,-3],type='response')) 0 1 0 600 0 1 0 20 > table(d$label,predict(d.rf.ub,newdata=d[,-3],type='response')) 0 1 0 600 0 1 0 20
めちゃくちゃオーバーフィッティングしてる気がしないでもないですが、改善したようです。ただし実際のconfusion matrixは全く一緒なので意味があるかどうかは微妙ですが。また、classwtの値を例えばc(1,20)やc(1,10)に変更してもc(1,30)の場合とほとんど変わらない模様なので、SVMにおけるclass.weightsとはちょっと訳が違うようです。これは前回紹介した@sfchaosさんのスライドでも指摘されていた事情が絡むのかもしれませんが。。。

そう言えば全くの余談。randomForest{randomForest}って「1つのカテゴリ型説明変数内に32個より多いカテゴリがあるとダメ」なんですが、その代わりダミー変数が32個以上あるのは問題ないんですね。。。最近試してて初めて知りました。
まぁでもこれって考えてみたら当たり前ですね。ランダムフォレストはmtryの個数だけ適当に説明変数を選び出してくるので、ダミー変数が32個以上あっても個々の木が繁り過ぎることはないんですが、カテゴリ型説明変数のカテゴリが32個以上あるとその説明変数を選択した個々の木の中での探索が2^32通りになるのでメモリから溢れるという。。。
ロジスティック回帰
glmでロジスティック回帰をやる時は、引数weightsに説明変数に対応するだけのクラス重み付けの生ベクトルを与えてやればOKです(rep関数とか使う必要があります)。
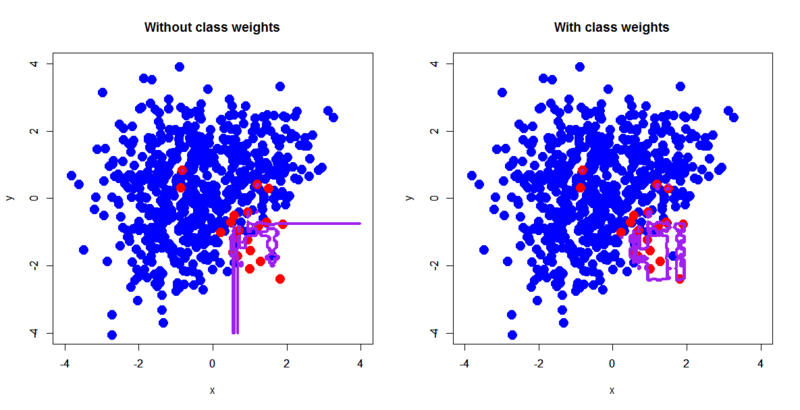
> d.glm<-glm(label~.,d,family=binomial) > d.glm.ub<-glm(label~.,d,family=binomial,weights=c(rep(1,600),rep(30,20))) # c(rep(1,600),rep(30,20))というのがポイント > out.d.glm<-predict(d.glm,newdata=pgrid,type='response') > out.d.glm.ub<-predict(d.glm.ub,newdata=pgrid,type='response') > par(mfrow=c(1,2)) > plot(d[,-3],pch=19,col=c(rep('blue',600),rep('red',20)),cex=2,xlim=c(-4,4),ylim=c(-4,4),main='Without class weights') > par(new=T) > contour(px,py,array(out.d.glm,dim=c(length(px),length(py))),xlim=c(-4,4),ylim=c(-4,4),col="purple",lwd=3,drawlabels=F,levels=0.5) > plot(d[,-3],pch=19,col=c(rep('blue',600),rep('red',20)),cex=2,xlim=c(-4,4),ylim=c(-4,4),main='With class weights') > par(new=T) > contour(px,py,array(out.d.glm.ub,dim=c(length(px),length(py))),xlim=c(-4,4),ylim=c(-4,4),col="purple",lwd=3,drawlabels=F,levels=0.5) > table(d$label,as.factor(round(predict(d.glm,newdata=d[,-3],type='response')))) 0 1 0 599 1 1 17 3 > table(d$label,as.factor(round(predict(d.glm.ub,newdata=d[,-3],type='response')))) 0 1 0 468 132 1 2 18
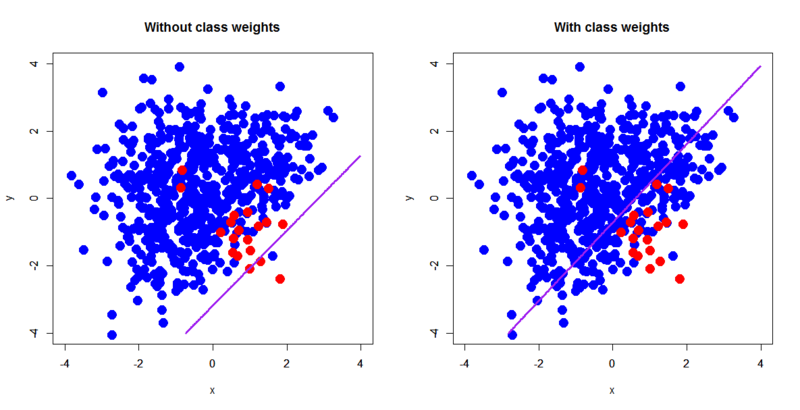
もちろん線形分離型の決定境界しか引けませんが、ちゃんとクラス重み付けを反映して改善されているのが分かります。ただしfalse alarmが大量に発生していることも見て取れます。この辺は別の問題ですよ、ということで。。。なおこれもweightsを変えてやるとこんな感じになります。
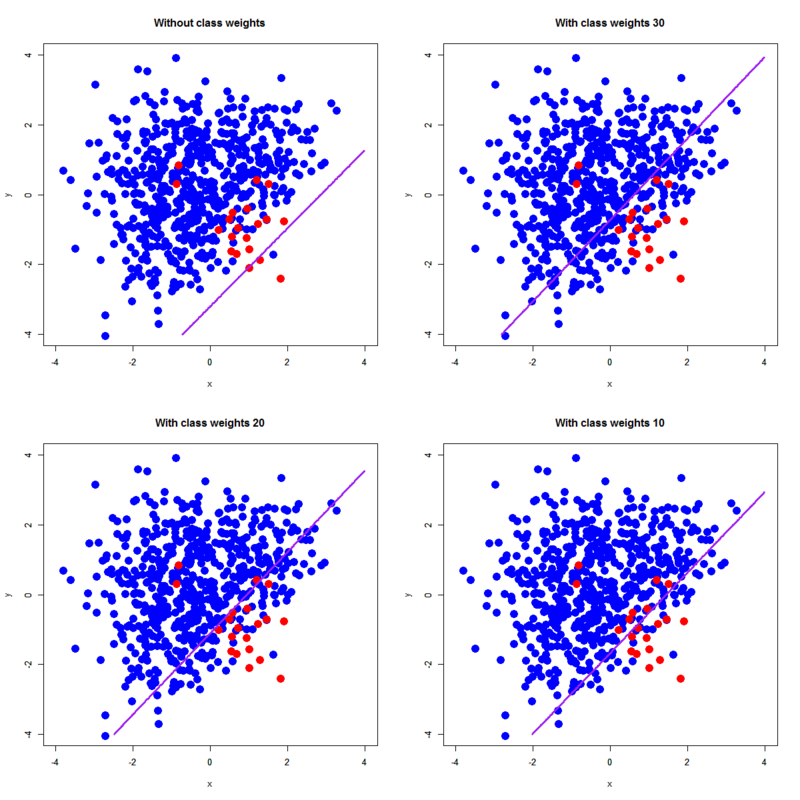
前二者とは異なり、決定境界の位置がほぼクラス重み付けに比例して動いている様子が分かります。ということは。。。線形分類器だとクラス重み付けに比例する形で決定境界が変わる一方で、非線形分類器だと比例するとは限らないのかも? ちょっと色々調べてみようかなと。