すっかりおじさんになってしまった身としては近年の日本のミュージックシーンに極めて疎くなって久しいのですが、最近になってAdoさん*1の楽曲に『過学習』というタイトルのものがあるということを知ったのでした。
一体どこで「過学習」なんてマニアックなテクニカルタームが存在することを知って、あまつさえ楽曲のタイトルにしようと考えたのか、というのが不思議で仕方ないのですが、機械学習や統計学を初めとするデータサイエンス領域の人々ぐらいにしか馴染みのなかった語がこうして人口に膾炙しているのかと思うとなかなかに感慨深いものがあります。
ということで、「過学習」とはどういうものであり、どのような場面で生じ、それをどうすれば避けられるか、という点について簡単にまとめてみることにしました。このテーマでは過去に何度もブログ記事を書いており、もはや何周目の話題なんだという感もありますが、温故知新ということでご容赦いただければと思います。また、記事中に理解不足やご認識の点などあれば何なりとご指摘くだされば幸いです。
過学習(過剰適合)とは
過学習(過剰適合)という現象は、基本的には「統計的学習モデルをデータに対して当てはめる際に真のシグナルどころかノイズにまで当てはまってしまい、かえってモデルの予測精度が低下する」ことを指します。これは直感的に分かるようで意外と分かりづらい概念であり、色々な説明の仕方がなされてきていますが、今のところ決定版といえるものはない気がしています。
なお僕個人が以前講演で用いた喩えは「大学入試で過去問ばかり丸暗記してすっかりそれに凝り固まってしまい、肝心の本番の入試の問題が解けない」というものですが*2、これはこれである程度の真実を捉えているかなと勝手ながら考えております。
分類モデルにおける過学習

喩えばかりでは分かりにくいので、どのような状況が生じたら過学習と呼ぶべきかを実際の例で見てみましょう。まず機械学習による分類モデルを用いて、上図の2つの二次元正規分布から生成した赤緑の2グループ*3のサンプルを分類するための決定境界を引くという問題を考えてみます。これには色々な考え方があり得るかと思いますが、素朴に考えれば下図のように「2グループを結んだ線分の垂直二等分線」をとるのが妥当でしょう。

ちなみにこれはロジスティック回帰でベタッと予測させたもので、素朴に考えた場合と同じ結果になっています。しかし、例えばSVMのような非線形分類モデルを用いて、さらにハイパーパラメータを意図的にいじれば、下図のような決定境界を描くこともできます。

……呪詛のオーラか何かのようで、ぶっちゃけ気持ち悪いですね(笑)。これだと、2グループを分類する決定境界としては不向きだと直感的に感じる方が多いのではないでしょうか。実際、この決定境界だと緑グループを左下に回り込んだ領域も「赤」に分類されてしまうわけで、あまりにも不自然です。けれども、同時にこの決定境界は緑グループのサンプル一つひとつにぴったり追随するようにフィットしています。
つまり、この分類モデルは「緑グループの(ノイズを伴ってばら撒かれた)サンプルの一つひとつに完璧にフィットする」ように「過剰に」学習した結果、明らかに全体のバランスが取れていない不自然な決定境界を引いてしまった、というわけです。その結果として例えば図中の左下隅のように「素朴に考えれば緑グループに分類されるはず」の領域までもが赤グループに分類されるという、誤った帰結に至っています。即ち、ノイズに過剰に適合するように学習したことで、却って予測性能が下がってしまったということです。
回帰モデルにおける過学習
前節では「分類」即ちサンプルを異なるグループに分けるための機械学習モデルにおける過学習について触れましたが、同様のことが「回帰」即ちサンプルに近似線(近似超平面)を引いて当てはめるための統計モデルにおいても言えます。例えば、黄色い本ことPRMLでもお馴染みの多項式フィッティングが恒例でしょう。PRMLに倣って、ここでは「3次関数に正規分布ノイズを加えて生成させたサンプルに対して3次多項式モデル(本来の次数)と9次多項式モデル(より柔軟性が高い)とを当てはめて比べてみる」ということをやってみます。

もう一目瞭然ですね。緑の曲線で表される3次モデルは個々のサンプルを微妙に外しながらも、全体としては綺麗にトレンドを捉えています。しかしながら、赤の曲線で表される9次モデルは個々のサンプルには忠実に当てはまっているものの、全体としては明後日の方向にぶっ飛んでしまっています。
これもまた、3次モデルに比べて9次モデルの方が「より多い回数曲げられる」*4という点で柔軟性が高いはずなのに、その柔軟性ゆえにノイズにまでフィットしてしまい、全体として見た場合の予測性能が損なわれる結果になっているというわけです。これは典型的な回帰モデルにおける過学習であり、実際にビジネスの現場でもいわゆる需要予測モデルにおいて同じ現象に陥ってしまっている事例を見たことが何度かあります。
過学習を避けるための交差検証
本質的には、先述したように過学習というのは「ノイズにまで学習してしまうことで未知データに対する予測精度が下がってしまう」現象です。では、これを避けるためにはどうしたら良いでしょうか? 最も単純なのは、ズバリ「モデルを学習させる際に毎回『別に取っておいた未知データ』を使ってその予測精度を評価し、ハイパーパラメータ類を変化させながら複数のモデルを学習させた上で、その結果が最も良かったモデルを選ぶ」という方法です。これを「交差検証」と呼びます。

やり方は色々あって、一番簡単なのは学習データをtraining + validationの2通り(もしくはtraining + validation + testの3通り)にランダムに分けて、trainingをモデル学習に使い、validationを予測精度の評価に使うというholdout法です(上図左)。ただ、これだとvalidationの選び方によってはバイアスが生じることがあります。
そこで、学習データをtraining + testの2通りにランダムに分けた上で、さらにtrainingをk個のグループにランダムかつ均等に分割し、そのうちk-1個のグループのデータをモデル学習に使い(training)、残った1個のグループのデータを予測精度の評価に使う(validation)、というのをk回繰り返し、最終的にその予測精度指標をマージ(普通は平均)したものを得て、モデルの良し悪しの評価指標とする、というやり方をすることがあります(上図右)。いわゆるk-fold法です。
分類モデルでも回帰モデルでも、基本的にはこれらの交差検証を用いることである程度以上過学習を避けることが可能です。時系列データだとちょっと注意が必要ですが*5、やはり交差検証を行うことで過学習を避けられます。これは大学入試の喩えでいえば「勉強の成果があったかどうかを検証するために、模試で未知の問題を解いてみてその点数を評価する」のと同じことです。模試の点数が毎回良かったからといって本番の大学入試も必ず上手くいくとは限りませんが、それでも良い下馬評にはなるはずです。
ビジネス(マーケティング)における、過学習のような現象
ここまでは分類モデルや回帰モデルといった統計的学習モデルの話題をしてきましたが、最後に「ヒトによるビジネス上の意思決定」においても過学習めいた現象が起こり得る、という話をしておきます。
これは8年前のブログ記事で例示したものですが、要は「ビジネスの現場においてマーケティング施策を多数打ち出しつつ高頻度でPDCAサイクルを回してしまうと、実際に長期的にKPIを向上させている施策がどれかが分かりづらくなり、結果として目先のノイズに一喜一憂しながら誤った方向に向かってしまう」というお話です。誤った施策指標ばかり追い続けたがために、一生懸命仕事をこなしているにもかかわらずどんどん経営上のKPIが下降していく……となるともはや悪夢そのものでしょう。
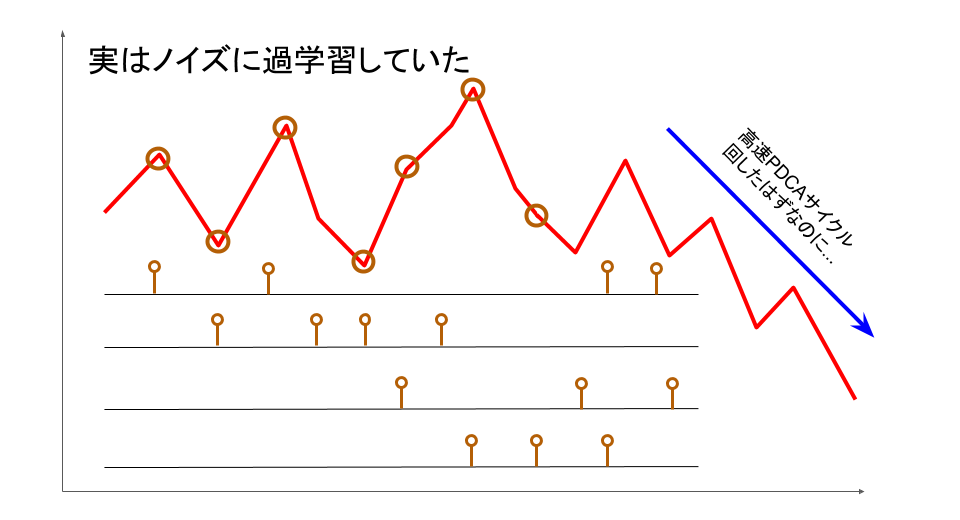
しかしながら、この構図に当てはまるビジネス上の実例を実際に見聞した回数は、冗談ではなく五本の指では数え切れません。分類や回帰といった数値データに基づく統計的学習モデルに限らず、経験知・暗黙知によっているヒトの学習にもまた過学習が起き得るのだとすると、これほど厄介なことはないと思われます。
流石に、ヒトの学習や意思決定に対してどのようにすれば過学習を回避し得るか、については僕も定見を持ち合わせてはいません。交差検証しようにも、例えば経営上の意思決定とかであれば「一回性」が高過ぎることもあり、なかなかに難しいところがあります。けれども、少なくとも「高速PDCAサイクル」にこだわり過ぎて目先のノイズに一喜一憂する事態を避け、出来るだけ中長期のトレンドにフォーカスすることで、これを避けることはある程度可能なのではないかと思われます。
いずれにせよ、何かしらの経験(数値データであれ個々のヒトの意思決定者の見聞であれ)に基づいて学習し、何かしら意思決定(分類であれ回帰であれヒトの取捨選択であれ)するという行為には過学習という現象が生じ得る、ということなのでしょう。データ分析を生業とし、そこからビジネス上の戦略を立案するという業務を担っている我が身としては、改めて深く肝に銘じるものです。
*1:『うっせぇわ』の人&檻の中で歌う人という認識しかないですごめんなさい
*2:この喩えは僕の講演が初出ではなくて、確か『コンピューターで「脳」がつくれるか』でも類似の表現がなされていたかと思います
*3:色覚次第では見づらい方もいるかと思うので補足しておきますと、右上が赤、左下が緑です
*5:トレンド・季節調整付き時系列データの回帰モデルを交差検証してみる - 渋谷駅前で働くデータサイエンティストのブログ