以下のメタアナリシス論文がしばらく前に話題になっていました。
このようなメタアナリシスを紐解くことで検定力・効果量がどういうものかという理解も進むのではないかと思われますので、以前の機械学習系論文の輪読まとめと同様に全引用or全訳にならない程度にまとめてみることにします。また斜め読みに近いまとめなので、間違っているところがチラホラあるかと思います。お気付きの際はコメント欄でも何でも良いのでご指摘下されば幸いです。
- アブストラクト
- この研究の目的は何か
- この論文では何を研究結果として報告しているのか
- メタアナリシスの対象になったのは何か
- どのようにしてデータを抽出したのか
- どのような手法でメタアナリシスを行ったのか
- メタアナリシスの結果はどうだったのか
- 著者らの考察・見解
- 感想と補足
アブストラクト
We have empirically assessed the distribution of published effect sizes and estimated power by analyzing 26,841 statistical records from 3,801 cognitive neuroscience and psychology papers published recently. The reported median effect size was D = 0.93 (interquartile range: 0.64–1.46) for nominally statistically significant results and D = 0.24 (0.11–0.42) for nonsignificant results. Median power to detect small, medium, and large effects was 0.12, 0.44, and 0.73, reflecting no improvement through the past half-century. This is so because sample sizes have remained small. Assuming similar true effect sizes in both disciplines, power was lower in cognitive neuroscience than in psychology. Journal impact factors negatively correlated with power. Assuming a realistic range of prior probabilities for null hypotheses, false report probability is likely to exceed 50% for the whole literature. In light of our findings, the recently reported low replication success in psychology is realistic, and worse performance may be expected for cognitive neuroscience.
(全訳)
この研究では、近年出版された3801報の認知神経科学及び心理学分野の論文に含まれる26841件の統計分析結果を分析することで、報告された効果量とそこから推定される検定力の分布について経験的手法に基づくメタアナリシスによって評価した。それらの論文で報告された効果量の中央値は、統計学的に有意であると報告されたものについてはD = 0.93(四分位間範囲は0.64-1.46)、有意でないと報告されたものについてはD = 0.24 (0.11-0.42)であった。(Cohenの)小・中・大のそれぞれの効果量を検出するための検定力の中央値はそれぞれ0.12, 0.44, 0.73であり、過去50年間で何も改善されていないという事実を反映している。これはサンプルサイズが小さいままであることが原因である。真の効果量が同程度だとすると、心理学分野に比べて認知神経科学分野の方が検定力で劣っている。論文誌のインパクトファクターは検定力に対して負の相関を示した。帰無仮説の事前確率の現実的な範囲を想定するに、今回対象とした論文全体で偽陽性(間違って統計学的に有意であると判定されること)を報告している確率は50%を超えるとみられる。我々の知見に照らし合わせれば、近年報告されている心理学分野における「再現性が低い」問題は現実のものであり、認知神経科学ではもっとそのパフォーマンスは悪いものと予想される。
この研究の目的は何か
Introductionのところに事細かに書いてありますが、ざっくり要約するとこんな感じのことを研究目的として述べています。
近年多くの科学研究分野で『多くの研究結果について再現性が低い』(例えば文献1, 文献2, 日本語解説など)という問題が叫ばれており、実際そのような研究に資金を投じるのは無駄でしかない。そこでこの研究では認知神経科学及び(実験)心理学分野に絞って、テキストマイニング手法を用いて効率よくデータを採取することで大規模なメタアナリシスを行い、そもそもそれらの研究が総体としてどれくらいの確率で間違った結果を報告している可能性があるかを探った。
この論文では何を研究結果として報告しているのか
上にも書きましたが、要はメタアナリシスです。メタアナリシスの詳細については様々なテキストや資料がありますが、手前味噌ながらお求めやすいものでいうと岩波DS第5巻の野間先生による「医学研究におけるメタアナリシス」という記事も参考になるかと思います。
様々な説明が可能かと思いますが、イメージとして一番近いのは以前こちらの記事で取り上げたカイ二乗検定の統合でしょうか。
一つ一つの統計分析の精度が十分でない場合に、複数の統計分析をマージすればそれだけ精度が向上してより正確な結論が導き出される、というのがメタアナリシスの目指すものです。ただし、今回はその趣向を少し変えて「心理学・認知神経科学分野の論文がどれくらいの信頼性ある統計分析結果を報告しているか」を分野全体として見積もる、というところを目指したとのことです。
メタアナリシスの対象になったのは何か
心理学・認知神経科学分野の以下のジャーナルに2011年1月〜2014年8月の間に掲載された論文3801報*1に記載された、26841件の統計分析結果です。
| 誌名 | 5年IF | 統計分析件数 | 論文数 | 統計分析件数/論文数 |
|---|---|---|---|---|
| A. Psychology | ||||
| Psychological Science | 6.16 | 2208 | 387 | 5.7 |
| Cognitive Psychology | 5.508 | 493 | 53 | 9.3 |
| Cognition | 5.088 | 2505 | 316 | 7.9 |
| Acta Psychologica | 3.016 | 769 | 161 | 4.8 |
| JECP | 3.353 | 1913 | 275 | 7 |
| B. Neuroscience | ||||
| Nature Neuroscience | 17.15 | 1212 | 121 | 10 |
| Neuron | 16.485 | 834 | 79 | 10.6 |
| Brain | 10.846 | 584 | 75 | 7.8 |
| The Journal of Neuroscience | 7.87 | 5408 | 621 | 8.7 |
| Cerebral Cortex | 8.372 | 1744 | 252 | 6.9 |
| Neuroimage | 6.956 | 971 | 193 | 5 |
| Cortex | 5.389 | 1508 | 198 | 7.6 |
| Biological Psychology | 4.173 | 1338 | 205 | 6.5 |
| Neuropsychologia | 4.495 | 2089 | 354 | 5.9 |
| Neuroscience | 3.458 | 1199 | 163 | 7.4 |
| C. Medical | ||||
| Biological Psychiatry | 10.347 | 1101 | 187 | 5.9 |
| Journal of Psychiatric Research | 4.46 | 468 | 94 | 5 |
| Neurobiology of Aging | 5.127 | 497 | 67 | 7.4 |
| 合計 | 26,841 | 3,801 |
(なお、どうでも良いCOIとして報告しておくと僕はこれらのジャーナルにはただの1報も載せたことはありません。ボンクラ研究者だったもので泣)
どのようにしてデータを抽出したのか
Methodsのところに最初に細かく書いてありますが、PDFで論文本文を上記の各ジャーナルの各巻から最大20報ずつ(これが一括ダウンロードの制限値とのこと)取得してきて、その上でMatlabコードで正規表現を駆使したコードを書いて全自動で
- t検定のt値
- その自由度df*2
の値を抽出するようというスクレイピングを行ったそうです。これが結構難物で、パフォーマンスのチェックのためにまずランダムに100報の論文を選んだ上で最初に手作業でt値と自由度のデータを集め、その上で上記のMatlabコードでスクレイピングした結果と照合して、合っているかどうかをさらにコルゴモロフ=スミルノフ検定で(抽出してきた自由度の分布が一致しているかどうか)確認したとのこと。苦心の跡がFig. 1に見えます(笑)。
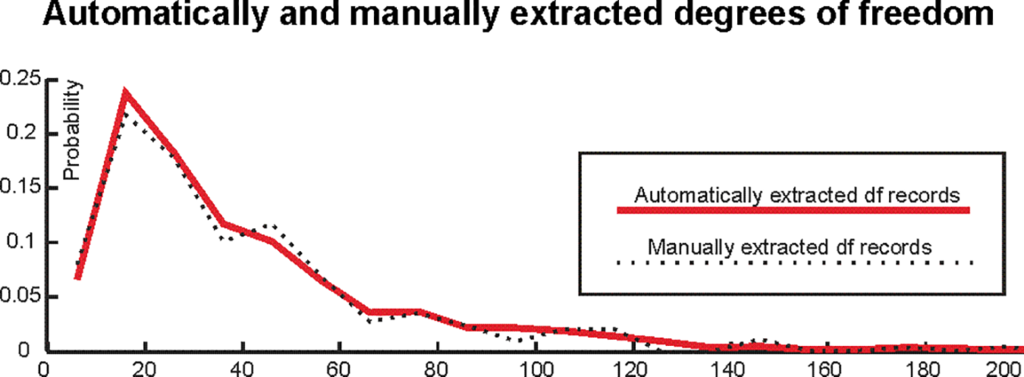
(Fig 1. The distribution of automatically and manually extracted degrees of freedom records (“df records”))
どのような手法でメタアナリシスを行ったのか
この論文で最も注目されているのはFRP (false report probability)の下限を定めることです。これはIntroductionでも細かに述べられているように、通常の偽陽性(false positive)とは若干異なり「統計的に有意(帰無仮説が棄却される)な場合に帰無仮説が真である確率」であり、一言でいえば「誤って偽陽性を報告している確率」です。これの下限を知ることで「最もマシな場合にどれくらいの論文が偽陽性を報告してしまっているか」が分かるという塩梅です。ちなみに論文中では対立概念として「統計的に有意な場合に対立仮説が真である確率」としてTRP (true report probability)についても言及されています。FRP / TRPはベイズの定理から単純に導き出すことができ、詳細がS1 TextのSection 5にあります。
そのFRPですが、具体的なモデルとしてMethodsの最後に以下のような式として与えられています。
はCohenの「小さな効果量」(small effect size)に対応する検定力、
は「大きな効果量」(large effect size)に対応する検定力、
はそれぞれ小さな / 大きな効果量である確率(和が1になる)です。
は
(帰無仮説vs.対立仮説)のオッズ比(これはそもそも論としてどれくらい帰無仮説が棄却されて対立仮説が採択されるべきかというバイアス的な要素を表し、1 : 1ならその確率は50% : 50%ということ)で、
は有意水準です。これによって、例えばジャーナルごとにFRPを求めることが可能になるはずだというわけです。
この式からFRPを求めるには、パラメータとして帰無仮説vs.対立仮説のオッズ比、検定力、効果量、そして効果量の大小どちらになるかの確率というデータが必要になります。最初のオッズ比は後でこちらから動かすパラメータなのでデータとしては要りませんが、残りの3つは上記の論文スクレイピングデータから求める必要があります。詳しい理論的なポイントは例えば和書だと以下の書籍にも書いてありますが、
基本的には論文スクレイピングデータに含まれるt値と自由度dfさえあれば、効果量Dの実測値を求めることは可能です。効果量であるCohen's d (D)の定義は以下のブログ記事でも紹介しています。また例えばこちらの資料なども分かりやすいかと思います*3。
これとt統計量の定義とを組み合わせて式変形すれば、簡単に論文上で報告されているt値から効果量Dを求めることができます。具体的にはS1 TextのSection 2に説明があるので、そちらをお読みください。ちなみに1標本t検定(もしくは対応のある2標本t検定)と独立した2標本t検定とが今回の対象文献全体ではごちゃごちゃに混じっていているので、それぞれの確率で加重平均したものをDとするみたいな補正をかけています。
そして、効果量Dと自由度dfがあれば、今度は非心t分布のパラメータが決まるのでこれに基づいて検定力(power)を求めることが可能になります(論文中では別の文献が引用されていますが、調べた範囲ではこちらの文献にその方法の説明があります)。これもS1 TextのSection 3にその詳細の説明があるので、興味のある方はそちらをどうぞ。なおこの後のFRPの計算のところでも特定の自由度dfと効果量Dとの組み合わせの確率に基づいて加重平均したものを算出するという補正をかけています。また、ここではCohenの古典的分類に従ってsmall (d = 0.2), medium (d = 0.5), large (d = 0.8)の3カテゴリに対応する検定力を求めるようにしています。
で、何でこんなまだるっこしいことをしたのかというと、結局「t検定関連のパラメータしか報告しない論文だらけの中で検定力を求めるための間接的証拠をできる限り集めて、そこから可能な限りより正確な検定力分析を行いたかった」ということのようです。そのアイデアの帰結がFRPという指標になったんでしょうかね。
ところで、非心t分布を伴う検定力分析の式は煩雑なのでここでは割愛しますが、直感的にも分かるように「検定力は自由度dfが小さければ同様に小さくなる」(=偽陽性を踏んで間違った結論に到達する可能性が高くなる)という性質のものです。これは後で重要なポイントになります。
メタアナリシスの結果はどうだったのか
Fig. 2に初歩的な分析結果がざっくりまとめられています。

(Fig 2. Degrees of freedom and effect size (D-value) distribution in the literature)
Aは自由度dfの分布。統計的に有意な結果でも、有意でない結果でも、自由度dfの最頻値mode = 15だったとのこと。Bは効果量Dの分布。論文中で報告があった2185件の効果量Dの分布と、報告がなかったので著者らがt値と自由度dfから推定した26841件の効果量Dの分布は、有意・有意でない問わずほぼ一致したとのこと。面白いのがCで、「効果量Dと自由度dfの2軸に対して個々の論文がどのように分布するかを濃淡プロットにした」もの。ボリュームゾーンがに来ており、しかも赤い太線「有意」のボーダーよりすぐ右側と、青い破線「有意でない」のボーダーよりすぐ左側とに不自然に論文が集中しているのがよく分かります(本来なら均等に分布しているはず)。ここで論文中では
オッズ比についてのコメントが付されています。曰く「
オッズ比が1 : 1(特にバイアスに類する要素なし)であれば赤い太線のすぐ左側にももっと論文が集中していても良いはずである」。
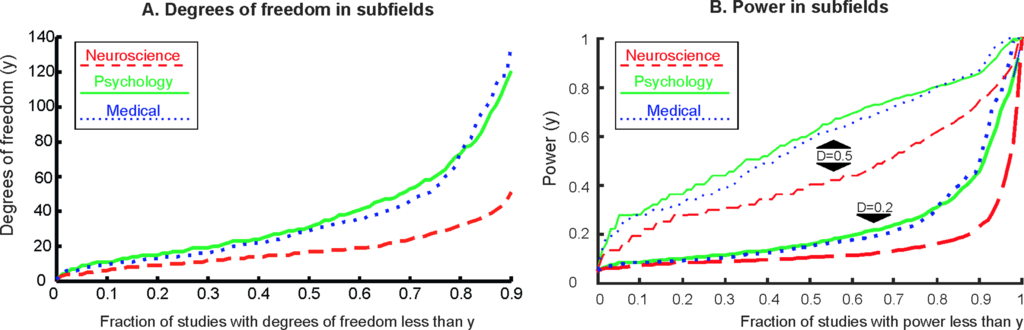
(Fig 3. The cumulative distribution of degrees of freedom and power)
Fig. 3は自由度dfの統計分析結果ごとの累積分布を示したものです。Aは純粋に自由度を累積分布にして3分野に分けたもので、医学・心理学に対して認知神経科学が極端に自由度が低い(=サンプルサイズが小さい / 被験者が少ない)ことが分かります。Bはmedium sizeの効果量(0.5)とsmall sizeの効果量(0.2)に対応する検定力の統計分析結果ごとの累積分布を3分野に分けてプロットしたもので、これも認知神経科学が最も低いです。
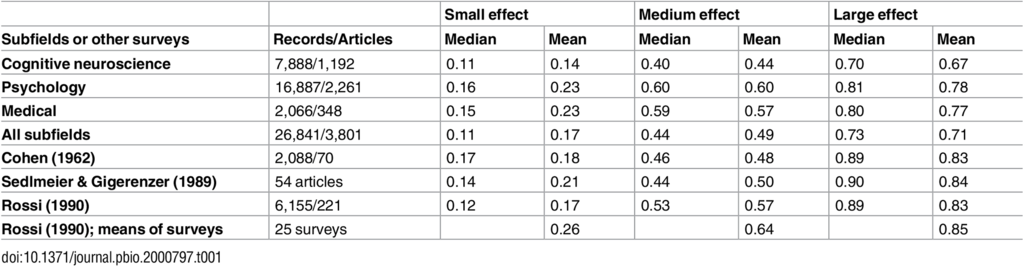
(Table 1. Median and mean power to detect small, medium, and large effects in the current study and in three often-cited historical power surveys)
上の方でも述べたように、有意水準・自由度・効果量が分かれば検定力は必ず求まります。その検定力をsmall, medium, largeの3カテゴリの効果量Dに対して今回対象とした論文の分野ごとに分けてまとめたものがTable 1です。これまた認知神経科学が一番低く、なおかつCohenが50年以上も前の1962年に70報の論文に含まれる2088件の統計分析結果から算出した検定力の値をいずれも下回っていることが分かります。
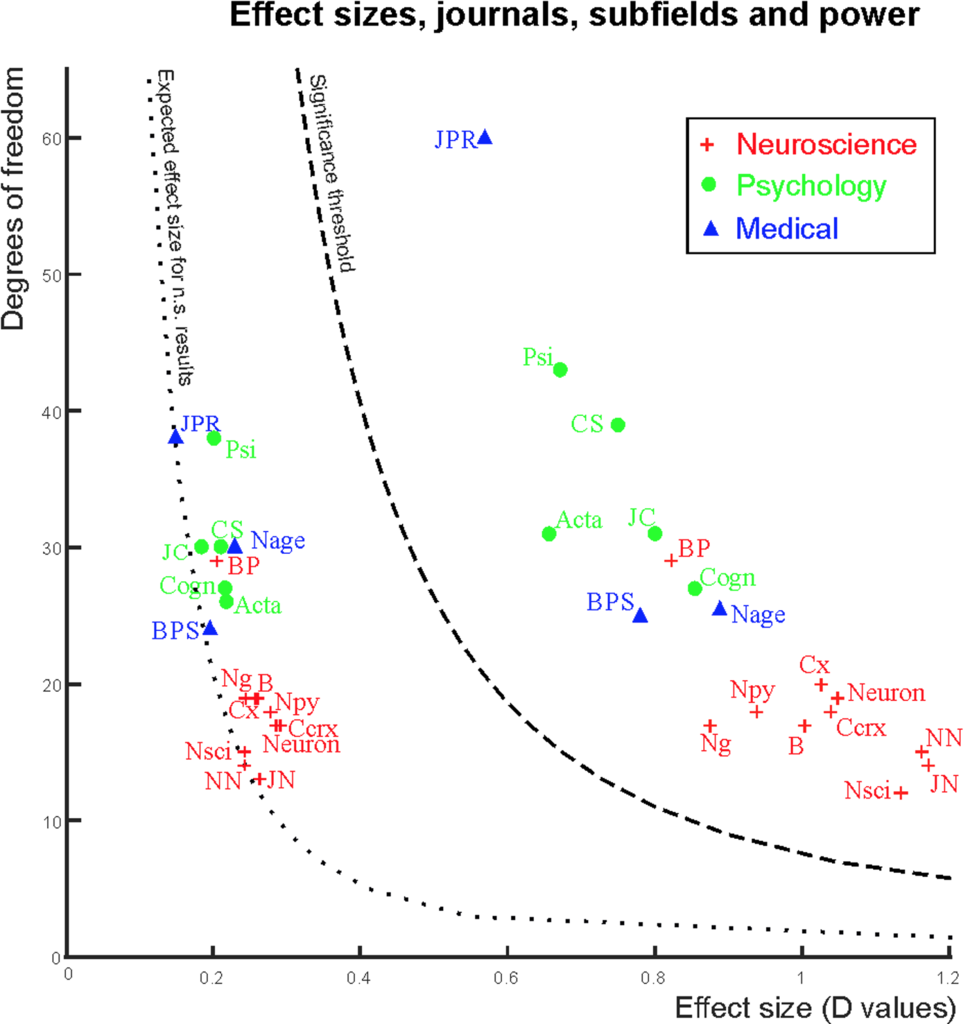
(Fig 4. Power in journals and subfields)
Fig. 4は今回対象とした各々のジャーナルが、効果量と自由度との2軸上にどうプロットされるかを表したものです(いずれもジャーナルごとの中央値)。既にFig. 3で示されたように、認知神経科学が自由度で一番低いところに分布していることが見て取れます。上の方で説明したように、自由度が低ければ検定力も低くなるため、FRPが高くなる=統計学的検定で間違った結論を導きやすくなるわけで、認知神経科学分野はその傾向が強いということが著者らのコメントとして付されています。
また、各ジャーナルのインパクトファクターと検定力の中央値とが「負の相関」を示す、ということも述べられています。これは言い方を変えると「皆が論文を載せたくなるジャーナルほど検定力が低い=偽陽性で間違った結論を載せている可能性が高い」ということにもなります。
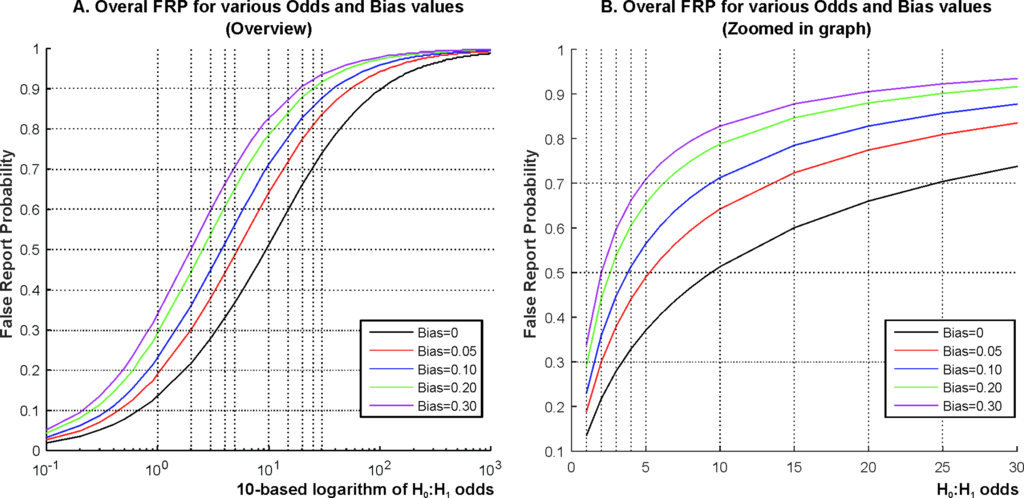
(Fig 5. Lower estimates of FRP for various H0:H1 odds and bias values)
最後に、Fig. 5はFRPの推定値をオッズ比を動かしながらプロットしたものです。ここでbiasというパラメータが登場しますが、論文中では「様々な実験上の都合で統計学的には本来有意でない結果が有意であるという結果になってしまう要因を表すもの」だとコメントされており、例えばこれが0.1なら本来有意でないはずの結果のうち10%が実験上の都合で有意となってしまうという状況を表すとのことです。ちなみにここでは「研究者による恣意的なサンプルの取捨選択(選別)やモデルの変更、もしくはデータの前処理の良し悪しや、ひどい場合は例えばp = 0.058をp < 0.05と言い張るというような改竄」と列挙されています。さらに加えて「出版バイアスやデータの捏造・改竄も含む」とのこと。
ともあれ、biasを考慮した上でFRPのシミュレーションを行うわけですが、そもそも論としてオッズ比というのは基本的には経験的には決まりません。ただ、論文中では今回の議論のきっかけとなった「再現性検証プロジェクト」を手がけているOpen Science Collaborationが(追試実験を行った結果として)提案している「心理学分野では13 : 1」という数字をひとつの目安としています。
その上でまずオッズ比の対数とFRP(偽陽性を報告してしまう確率)を片対数プロットで5パターンのbiasごとに示したものがAで、これを
オッズ比 = 13前後のゾーンに拡大したのがBです。13だと、bias = 0であってもFRPが0.5を超えています。言い換えると「再現性検証プロジェクトの結果を鑑みれば今回対象としたジャーナルに掲載されている論文が偽陽性(本来は統計学的には有意ではないのに有意に見えてしまっているもの)を報告してしまっている確率は50%以上」だということになります。
著者らの考察・見解
メタアナリシスの結果を見ればお分かりかと思いますが、著者らは3分野の中でも特に認知神経科学分野を問題視しているようで、
- 脳機能画像のような実験は予算がかかるので、予算を惜しんで被験者を少なく済ませようとする
- データ分析に複雑なソフトウェアやパッケージを異様に高い柔軟性(それ故にちょっとの変更で大きく結果が変わる)のもとで使っているせいで、様々な文書化もされていなければ場合によっては理解すらもされていないようなプラクティスに基づいて間違っていたり再現性のない分析を平気で回してしまうことになりやすい*4
- サンプルサイズが小さい(被験者数が少ない)と偽陽性で有意に見える結果が得やすいがために、少ない被験者で実験を済ませることにこだわりがち
- 医学系に比べると間違った結果が大きなリスク(例えば被験者や患者が死亡するなど)になりにくいので、多少信頼性の低い結果でも論文にしようとしてしまうなどのバイアスが強い
- インパクトファクターの高いジャーナルほど検定力が低いという点からは、それらのジャーナルが統計的に有意な知見をことさらに要求した結果として「素晴らしい結果」に見える偽陽性を報告する論文を誘発している可能性が推測される
と指摘しています。一方で、著者ら自身が今回のメタアナリシスに対する注意点として以下のポイントを挙げています。
- テキストマイニングで自動抽出したものであるため、個々の統計分析結果が「主要な結果」なのか「副次的なもの」なのかそれこそ「試験段階のもの」なのかは区別されていない
- 観測バイアスがかかっている可能性は否定しきれない
- 研究結果の種類(例えば実験デザインなどの)も自動抽出ゆえ区別していないため、種類ごとに効果量・自由度・検定力の分布が異なっていて結果を歪めている可能性がある
- 今回報告したのはあくまでも自動抽出した自由度に基づくt検定の混合モデルの検定力でしかない
- 自動抽出では全ての有意「でない」p値を取得することはできていない
- そもそも下位領域ごと(それこそ個々の研究グループごと)できちんとやっているところとやっていないところとの差が大きいはずであり、一般化するには注意が必要である
そして最後の最後に、著者らは「再現性が低い」問題に対して以下のように改善策を提案しています。
感想と補足
メタアナリシス手法のところで見たように、色々と著者らが想定する前提のもとに補正をかけたりしているので、その辺はまだ議論が残るところだと思います。特定の4年間の特定のジャーナル群に限定したデータセットによる結論だという点にも留意すべきでしょう。最近チラッと見かけた論文ではきちんと事前に検定力分析を行ってサンプルサイズを決定した上で実験に臨んだという記述をしているものもあったので、そういう「きちんとした論文」とそうではない論文とでどう異なるか?を調べることも必要なのではないかと思われます。
ところで、手法的には正直言ってそれほど複雑なメタアナリシスはしていないなという感想を持ちました。むしろ著者らも強調していますが、やはりスクレイピング作業の方が大変だったんじゃないのかなと(笑)。データ分析を生業とする身としては是非見習いたいところです。非心t分布の話題を論文で読んだのは恥ずかしながらこれが初めてでした。意外と勉強しておくものですね。。。
なお、この論文の内容そのものに指摘や異論がおありの方はこのブログではなく著者であるSzucs, Ioannidis宛てにPLoS Biolのコメント欄にて直接投稿されるとよろしいかと思います。お粗末様でした。

