パッケージユーザーのための機械学習(5)：ランダムフォレスト - 渋谷駅前で働くデータサイエンティストのブログ

（※はてなフォトライフの不具合で正しくない順番で画像が表示されている可能性があります）

さて、こんな記事をクリスマス・イヴのプレゼントにするのはアレなんですが（笑）、教師あり学習＆分類器系では一旦これでシリーズを〆る予定です。

トリを飾るのはランダムフォレスト。アンサンブル学習の代表選手ですね。「ランダムフォレスト最強」とか言っちゃう人が多いらしいんですが*1、そういう人にはぜひ今回（と次回予定の5回分まとめ）の記事を読んでもらいたいなぁと思います。

今回の参考文献もピンクの薄い本です。pp.193-197に決定木、バギング、アダブーストの後にランダムフォレストの説明があります。

はじめてのパターン認識

作者: 平井有三
出版社/メーカー: 森北出版
発売日: 2012/07/31
メディア: 単行本（ソフトカバー）
購入: 1人クリック: 7回
この商品を含むブログ (4件) を見る

他だと、例えばPRMLにもランダムフォレストの説明が載ってますが猛烈にまだるっこしいので、むしろ杉山本とか良いと思います。

イラストで学ぶ機械学習最小二乗法による識別モデル学習を中心に (KS情報科学専門書)

作者: 杉山将
出版社/メーカー: 講談社
発売日: 2013/09/18
メディア: 単行本（ソフトカバー）
この商品を含むブログ (2件) を見る

「ランダム森」の訳語は辛いですが（笑）、僕が思うに説明の簡潔さではこちらが一番だと思います。pp.93-99における決定木*2の説明からランダムフォレストに入るところの分かりやすさは良いですね。そうそう、そもそもこのシリーズの第1回が決定木だったので、そちらも併せてどうぞ。

まずRでどんなものか見てみる

いつも通りランダムフォレストの雰囲気だけ見るということで、これまでと同様にGitHubに置いてある以前のサンプルデータを使いましょう。すっかりお馴染み、コンバージョン(CV)に効くアクション(a1-a7)を探り出そうというテーマで用意されたデータです。dという名前でインポートしておきます。

Rでランダムフォレストと言えば、基本的には{randomForest}パッケージです。こいつをインストールして、以下のようにやってみましょう。以前の記事（Rで機械学習するならチューニングもグリッドサーチ関数orオプションでお手軽に）でtuneRF()関数でチューニングできると紹介してますので、これもついでにやってみます。

> require("randomForest")
Loading required package: randomForest
randomForest 4.6-7
Type rfNews() to see new features/changes/bug fixes.

> tuneRF(d[,-8],d[,8],doBest=T)
mtry = 2  OOB error = 6.43% 
Searching left ...
mtry = 1 	OOB error = 9.23% 
-0.4352332 0.05 
Searching right ...
mtry = 4 	OOB error = 6.6% 
-0.02590674 0.05 

Call:
 randomForest(x = x, y = y, mtry = res[which.min(res[, 2]), 1]) 
               Type of random forest: classification
                     Number of trees: 500
No. of variables tried at each split: 2

        OOB estimate of  error rate: 6.4%
Confusion matrix:
      No  Yes class.error
No  1399  101  0.06733333
Yes   91 1409  0.06066667
# まずはチューニングする：mtry=2が最適らしい

f:id:TJO:20131221170032p:plain

こんな感じでチューニングの結果が出ます。mtry=2つまり「個々の木ごとの特徴量選択は2つずつが最も良い」ということなので、これをrandomForest()関数の引数に充てます。

> d.rf<-randomForest(cv~.,d,mtry=2)
# mtry=2を引数にしてrandomForest()関数で分類する

> print(d.rf)

Call:
 randomForest(formula = cv ~ ., data = d, mtry = 2) 
               Type of random forest: classification
                     Number of trees: 500
No. of variables tried at each split: 2

        OOB estimate of  error rate: 6.37%
Confusion matrix:
      No  Yes class.error
No  1403   97  0.06466667
Yes   94 1406  0.06266667
# OOB誤差が6.37%とまずまず

> importance(d.rf)
   MeanDecreaseGini
a1        20.320854
a2        11.490523
a3         2.380128
a4       203.135651
a5        75.415005
a6       783.553501
a7         2.679649
# 決定木同様に変数重要度が出せる。これもまた重要

> table(d$cv,predict(d.rf,d[,-8]))
     
        No  Yes
  No  1409   91
  Yes   83 1417

# 分類正答率は94.2%とまずまず

この分類正答率94.2%というのは、これまで取り上げてきたSVMやニューラルネットワークよりも優れた数字です。ランダムフォレストが機械学習分類器としていかに優秀かが分かる数字ではないかと思います。

ランダムフォレストとは何ぞや

簡単に言えば「弱学習器を決定木とするバギング」です。バギングについては多分杉山本の説明から引用した方が分かりやすくて手っ取り早いと思いますので、p.97から抜粋。

① $j=1, \cdots, b$ に対して以下の処理を繰り返します。

(a) $n$ 個の訓練標本 ${(\mathbf{x}_i,y_i)}^n_{i=1}$ から、重複を許してランダムに $n$ 個選びます。

(b)こうして得られた標本を用いて、弱学習器 $\phi_j$ を求めます。

②すべての弱学習器 $\{\phi_j\}^b_{j=1}$ の平均を強学習器 $f$ として求めます。

$f(\mathbf{x}) \leftarrow \frac{1}{b} {\displaystyle \sum^{b}_{j=1}} \phi_j (\mathbf{x})$

これをそれっぽい概念図で表すと、よくあるこういう絵になります。

f:id:TJO:20131224120501p:plain

つまりブートストラップ法をうまく利用するというのがその肝です。ブートストラップ標本から計算負荷の軽い弱学習器をたくさん作って、ブートストラップ法よろしくその平均を取ることで、empiricalに精度が高いと期待される強学習器を作れる！というのがそのコンセプトなんですね。

そこで、その弱学習器としてまさに計算負荷の軽い決定木*3を選んでいるというのがランダムフォレストというわけです。

ただし、通常のバギングだと個々の決定木間の相関が高くなってしまい、分類精度の低下につながるので、ランダムフォレストでは識別に用いる特徴をあらかじめ決められた数（これが{randomForest}パッケージで言うところのmtry引数）だけランダムに選択することで、相関の低い多様な決定木を生成できるようにしています（はじパタp.193）。{randomForest}パッケージだと、tuneRF()関数で最適なmtryの値をグリッドサーチで求めることができます。

そのアルゴリズムですが、例えばWikipediaには以下のように書かれています。

アルゴリズム

学習

学習を行ないたい観測データから、ランダムサンプリングによりB組のサブサンプルを生成する（ブートストラップサンプル）

各サブサンプルをトレーニングデータとし、B本の決定木を作成する

指定したノード数 $n_{min}$ に達するまで、以下の方法でノードを作成する

トレーニングデータの説明変数のうち、m個をランダムに選択する

選ばれた説明変数のうち、トレーニングデータを最も良く分類するものとそのときの閾値を用いて、ノードのスプリット関数を決定する

要点は、ランダムサンプリングされたトレーニングデータとランダムに選択された説明変数を用いることにより、相関の低い決定木群を作成すること。

パラメータの推奨値

$n_{min}$ : 識別の場合は1、回帰の場合は5

m: 説明変数の総数をpとすると、識別の場合は $\sqrt(p)$ 、回帰の場合は p/3

評価

最終出力は以下のように決定する

識別: 決定木の出力がクラスの場合はその多数決、確率分布の場合はその平均値が最大となるクラス

回帰: 決定木の出力の平均値

（wikipedia:Random_forest）

なお、発案者のLeo Breiman本人による解説記事のwebページが公開されているので、英語を読むのが苦にならない人はそちらも読んでみると良いでしょう。

Random forests - classification description

もちろん、ここに載っている要件を見ながらスクラッチからコードを組むというのも良い勉強になると思います。僕は面倒なのでやりませんが（笑）。

なお、ランダムフォレストはcross validationの一種とも言えるOut-Of-Bag (OOB) error rateによってその性能を評価することができます。これははじパタpp.194-195にも書かれていますが、要は「ある学習データについてその学習データが使われなかった決定木のグループを集めて部分森を構成した上でその学習データをテストデータとして分類してerror rateを算出する」ことで得られるものです。ちなみに{randomForest}パッケージだと「分類」のケースではOOB error rateですが、「回帰」のケースでは% variance explainedということで分散説明度が返されます。

そして、原理上は決定木と全く同じなので、「分類」「回帰」問わず変数重要度*4を定めることができます。これは{randomForest}パッケージならimportance()関数でチェックすることができますし、partialPlot()関数でプロットすることもできます。むしろこれを期待してアドホック分析などで使う人は多いんじゃないでしょうか。なお、変数重要度についてはこちらも良い資料になるかと。

Random Forestで計算できる特徴量の重要度 - なにかしらのメモ帳

ちなみに僕のやっつけ仕事みたいな原理の説明に比べて、こちらの記事の方がランダムフォレストの原理についてもっと分かりやすく描かれているのでお薦めです。

決定境界を描いてみる

では、いつも通りやってみましょう。非線形分離可能というのもランダムフォレストの利点なので、これまで同様XORパターンの分類をやります。これまたいつものようにGitHubからXORパターンのシンプル版、複雑版を持ってきて、それぞれxors, xorcという名前でインポートしておきます。

ちなみにこのデータでもチューニングすることはできますが、実はmtry=1でも2でも良いという結果になります。。。

> require("randomForest")
Loading required package: randomForest
randomForest 4.6-7
Type rfNews() to see new features/changes/bug fixes.

> xors$label<-as.factor(xors$label-1)
> xorc$label<-as.factor(xorc$label-1)
# labelを[0,1]に直す

> tuneRF(xors[,-3],xors[,3],doBest=T)
mtry = 1  OOB error = 3% 
Searching left ...
Searching right ...
mtry = 2 	OOB error = 3% 
0 0.05 

Call:
 randomForest(x = x, y = y, mtry = res[which.min(res[, 2]), 1]) 
               Type of random forest: classification
                     Number of trees: 500
No. of variables tried at each split: 1

        OOB estimate of  error rate: 3%
Confusion matrix:
   0  1 class.error
0 48  2        0.04
1  1 49        0.02
> tuneRF(xorc[,-3],xorc[,3],doBest=T)
mtry = 1  OOB error = 34% 
Searching left ...
Searching right ...
mtry = 2 	OOB error = 34% 
0 0.05 

Call:
 randomForest(x = x, y = y, mtry = res[which.min(res[, 2]), 1]) 
               Type of random forest: classification
                     Number of trees: 500
No. of variables tried at each split: 1

        OOB estimate of  error rate: 32%
Confusion matrix:
   0  1 class.error
0 33 17        0.34
1 15 35        0.30

> xors.rf<-randomForest(label~.,xors)
> xorc.rf<-randomForest(label~.,xorc)
# 普通にrandomForest()で分類する

> px<-seq(-3,3,0.03)
> py<-seq(-3,3,0.03)
> pgrid<-expand.grid(px,py)
> names(pgrid)<-c("x","y")
# 分離超平面を描くためのグリッドを作る

> plot(xors[1:50,-3],col="blue",pch=19,cex=3,xlim=c(-3,3),ylim=c(-3,3))
> points(xors[51:100,-3],col="red",pch=19,cex=3)
> par(new=T)
> contour(px,py,array(out.xors.rf,dim=c(length(px),length(py))),xlim=c(-3,3),ylim=c(-3,3),col="purple",lwd=3,drawlabels=F,levels=0.5)
# シンプルパターンで分離超平面を描く

> plot(xorc[1:50,-3],col="blue",pch=19,cex=3,xlim=c(-3,3),ylim=c(-3,3))
> points(xorc[51:100,-3],col="red",pch=19,cex=3)
> par(new=T)
> contour(px,py,array(out.xorc.rf,dim=c(length(px),length(py))),xlim=c(-3,3),ylim=c(-3,3),col="purple",lwd=3,drawlabels=F,levels=0.5)
# 複雑パターンで分離超平面を描く

> table(xors$label,predict(xors.rf,xors[,-3]))
   
     0  1
  0 50  0
  1  0 50

# シンプルパターンの分類正答率は100%

> table(xorc$label,predict(xorc.rf,xorc[,-3]))
   
     0  1
  0 50  0
  1  0 50

# 複雑パターンでも分類正答率は100%

f:id:TJO:20131224142939p:plain

シンプルパターンの場合と、

f:id:TJO:20140101221848p:plain

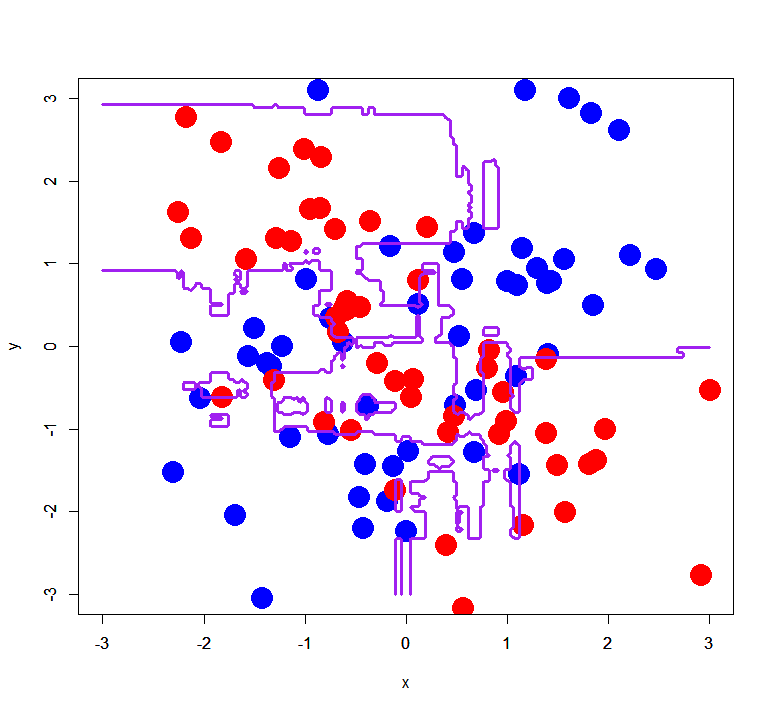
複雑パターンの場合。ちなみにこれだとマーカーがでか過ぎる気がしないでもないので、マーカーを小さくするとこんな風に見えます。

f:id:TJO:20131224143000p:plain

前者はともかく、後者は汎化のハの字もないくらいバリバリに過学習してる気がするんですが（笑）、まぁこんな感じです。何はともあれ、実はこれまでの機械学習分類器の中ではもっとも分類正答率が高い（どちらも100%）という結果になりました。

なお、randomForest()関数ではntrees引数でランダムフォレストとして生成する決定木の数を定めることができて*5、同時にplot.randomForest()関数でntreesに対するOOB error rateの変動を見ることができます。

> plot(xors.rf)
> plot(xorc.rf)

f:id:TJO:20131224143842p:plain

f:id:TJO:20131224143852p:plain

シンプルパターンだとすんなりOOB error rateが収束しているんですが、複雑パターンだと何だかふらついてる気がしなくもないですね。もしかしたら過学習してるのかもしれません。。。

最後に

ランダムフォレストは非常に強力な分類手法なんですが、いかなOOBに見られるような汎化が行われると理論的には言われていても、分離超平面の例を見ての通り学習データ次第では汎化が利かない可能性があるという点に注意が必要なんじゃないかと思ってます。というのも、結局は決定木の集合体である以上はどうしても「軸に平行」にしか（部分的ではあっても）分離超平面は引けないわけで。

そういう意味で言うと、OOB error rateによる評価も重要なんですがそれ以上に実データのcross validationによる性能評価が必要なんじゃないかなぁとか、汎化を優先するならSVMとか低バリアンスなモデルを使った方が良さそうだよね、というのが率直な感想です。