この記事は4年前の以下の過去記事の続きです。
大変遅まきながら*1、最近になって単変量時系列モデリングの手法としてARIMA / DLM以外にも幾つか方法があるのだということを知りました。一つは指数平滑法というかExponential Smoothing State Space Model (ETS)で、もう一つはこれをロバスト化したRobust ETS。
指数平滑法そのものについては日本語でも色々資料があるんですが(この辺とか)、例えば{forecast}パッケージのets関数に実装されている指数平滑状態空間モデルについてはweb上にはあまり詳しい日本語資料が見つからなかった*2ので、代わりに英文資料(7.7 Innovations state space models for exponential smoothing | OTexts)を貼っておきます。おそらくこれだけ読んでおけば十分だろうと想像します。
ということでこの記事は純然たる自分向けの個人的なまとめにつき、特に何も目新しい情報はありませんので悪しからずご了承くださいm(_ _)m
ETSについて、個人的にまとめておく
英文資料(7.7 Innovations state space models for exponential smoothing | OTexts)を読んで自分の中で理解したのは、
- より直近の過去値からの影響を重視し、過去になればなるほど指数関数的に影響が小さくなるモデル
- 普通の加法型誤差項だけでなく乗法型誤差項も可能なモデル
- 以上の制約のもとで状態空間モデルにまとめたもので、モデル推定は観測値ではなく状態値に基づく
ということなのかなと。これから直感的に分かるのは
- 直近の変動に対して追従しやすい
- 故に推定される信頼区間も未来になればなるほど広がりやすい
- 状態空間モデルなので異常値や欠損値に対して強い
といったところでしょうか。そう言えばCross Validatedにもこんな質問があるのを見つけました。
いつも通り炎上ラーニング大歓迎なので、どなたかツッコミを入れて下さると有難いです(汗)。
ARIMA
ここでは過去記事の2番目のデータだけを使うことにします。
> y1 <- rep(c(3,5,12,4),20) # 四半期周期のデータ > y2 <- 20+20*sin(seq(from=-0.5*pi,to=0,length.out=80)) # 何となく上昇トレンドをsineカーブで表してみる > y<-y1+y2+rnorm(mean=0,sd=3,n=80) # ランダム成分を加える > yt <- ts(as.numeric(y),frequency=4) # 四半期周期でtsオブジェクト化 > plot(yt)
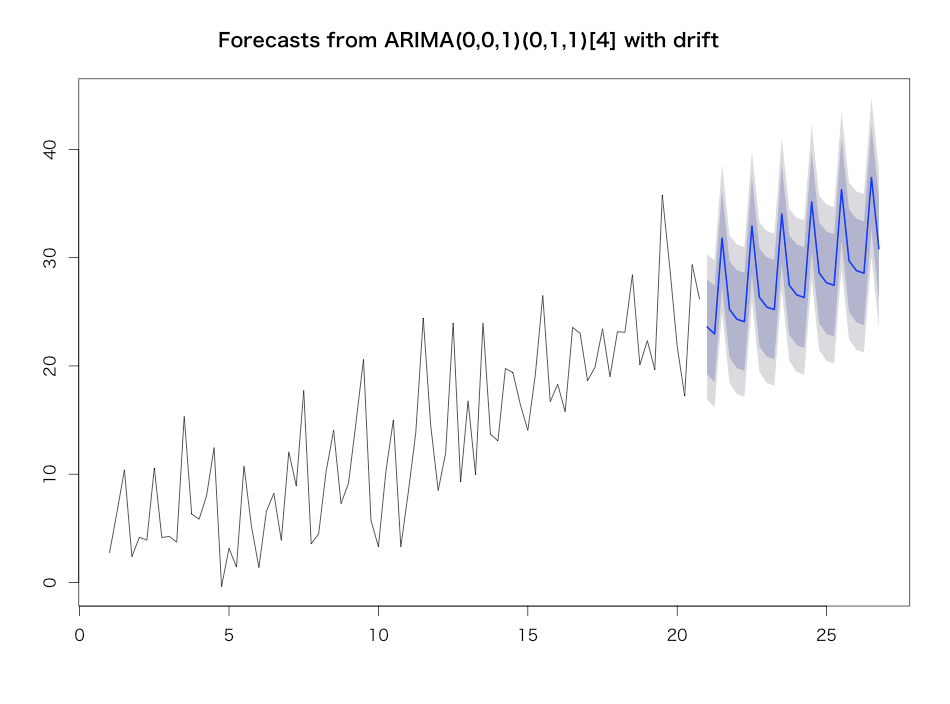
ARIMAについては既に取り上げた通りですが、一応やっておきます。以下の通りです。
> library(forecast) > yt.arima <- auto.arima(yt, trace=T, stepwise=T) ARIMA(2,0,2)(1,1,1)[4] with drift : Inf ARIMA(0,0,0)(0,1,0)[4] with drift : 450.4651 ARIMA(1,0,0)(1,1,0)[4] with drift : 426.0956 ARIMA(0,0,1)(0,1,1)[4] with drift : 415.295 ARIMA(0,0,0)(0,1,0)[4] : 451.6131 ARIMA(0,0,1)(1,1,1)[4] with drift : 416.7981 ARIMA(0,0,1)(0,1,0)[4] with drift : 452.0229 ARIMA(0,0,1)(0,1,2)[4] with drift : 416.8515 ARIMA(0,0,1)(1,1,2)[4] with drift : 419.1583 ARIMA(1,0,1)(0,1,1)[4] with drift : 417.5371 ARIMA(0,0,0)(0,1,1)[4] with drift : 415.8194 ARIMA(0,0,2)(0,1,1)[4] with drift : 417.5075 ARIMA(1,0,2)(0,1,1)[4] with drift : 419.8585 ARIMA(0,0,1)(0,1,1)[4] : 434.6375 Best model: ARIMA(0,0,1)(0,1,1)[4] with drift > plot(forecast(yt.arima, h=24))
ETS
ETSは同じ{forecast}パッケージのets関数でモデリングできます。
> yt.ets <- ets(yt, ic='aic', damped=T, allow.multiplicative.trend=T) > yt.ets ETS(A,Ad,A) Call: ets(y = yt, damped = T, ic = "aic", allow.multiplicative.trend = T) Smoothing parameters: alpha = 0.0328 beta = 0.0174 gamma = 0.0033 phi = 0.98 Initial states: l = 5.6907 b = -0.0767 s=-2.0606 5.8992 -1.2368 -2.6018 sigma: 3.2284 AIC AICc BIC 556.0804 558.6519 577.5187 > plot(forecast(yt.ets, h=24))
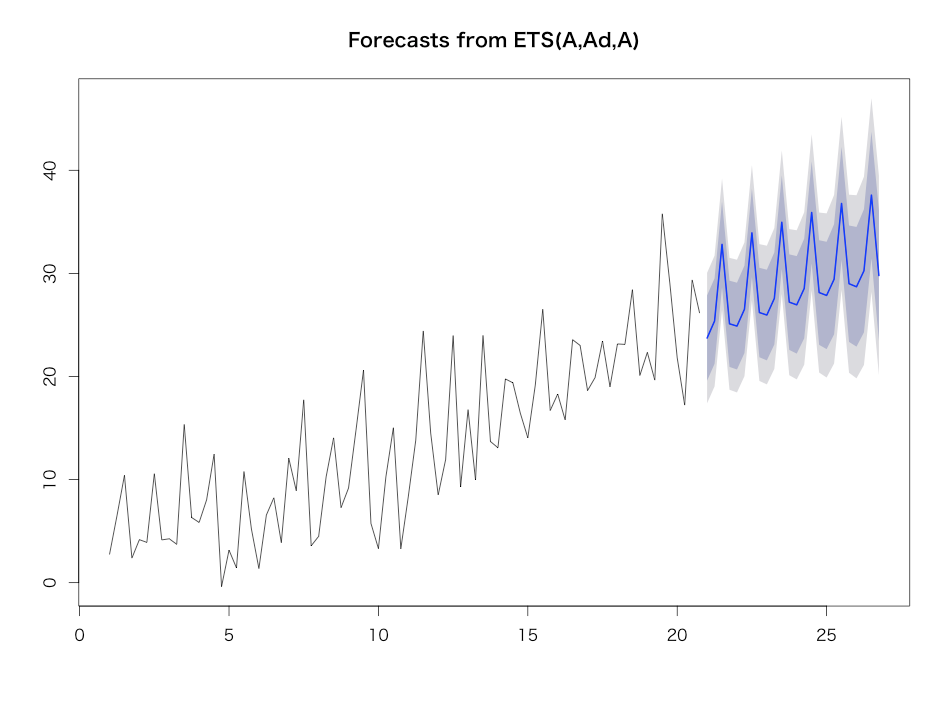
パッと見にはARIMAの結果とは大きく異ならないように見えます。実際の最尤推定値も0.0328と小さく、ARIMA並みに過去値が反映されるようなモデルになっているということなのかなと思います。
Robust ETS
これはworking paperが出ているのでそちらを参照した方が良いかと思います。ザッと適当に眺めた範囲で書くと、予測値の振れ幅に予め上限を定めておいてこれを超えた場合には棄却するというモデル更新則を用いているようです。これにより、状態空間モデルが本来持っている(予測値についての)ロバスト性を超えて、さらに事前に定めたハイパーパラメータkで与えられる範囲に予測値の変動を収められる、というのがここで言うロバスト性の意味するところなのかなと。
で、このRobust ETSはズバリ{robets}というCRANパッケージで提供されているので、これをインストールすれば簡単に試すことができます。上記のデータを用いて予測をやってみるとこうなります。
> library(robets) > yt.robets.aic <- robets(yt, damped=T, ic='aic') > yt.robets.aic ROBETS(A,Ad,A) Call: robets(y = yt, damped = T, ic = "aic") Smoothing parameters: alpha = 0.4996 beta = 0.0764 gamma = 0.0137 phi = 0.9676 Initial states: sigma = 1.4105 l = 4.9349 b = 0.1059 s=-1.8546 5.1491 -1.6622 -1.6324 sigma: 3.8464 robAIC robAICc robBIC 561.7189 562.2522 571.2470 > plot(forecast(yt.robets, h=24))
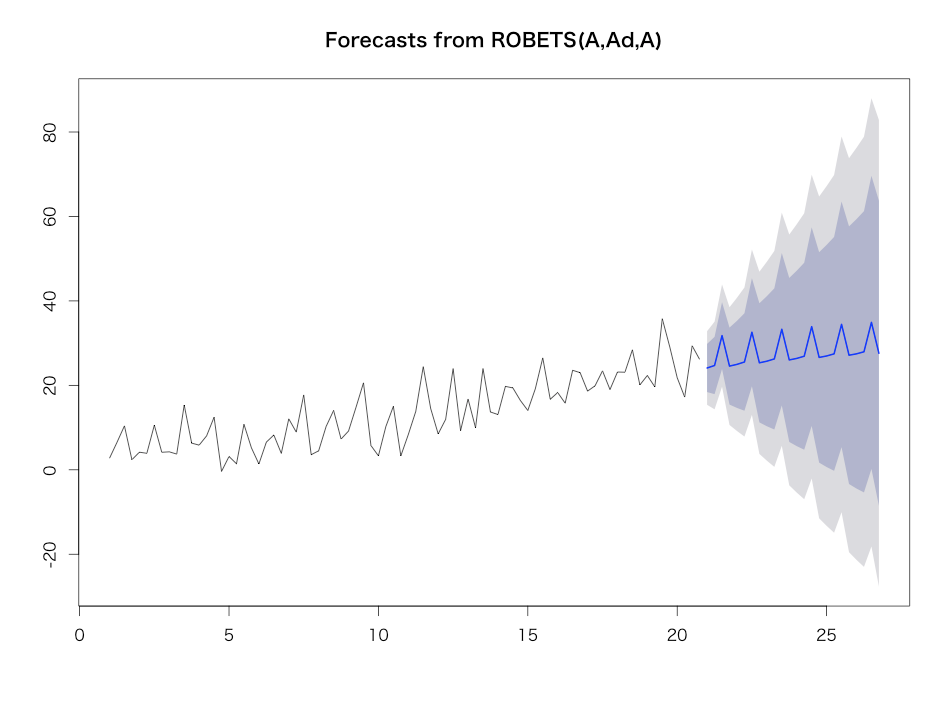
ものすごーく信頼区間が広がってしまいました。の推定値も0.4996と非常に大きくなっていて、過去値の影響がどんどん小さくなるモデルであることが分かります。ちなみにモデル選択基準を他のBIC, Robust AIC, Robust AICC, Robust BICにしてもこのモデルが必ず選ばれます。
そこで、普通に推定結果をplotしてETSとRobust ETSとでモデルを比べるとこうなります。
> plot(yt.ets) > plot(yt.robets.aic)
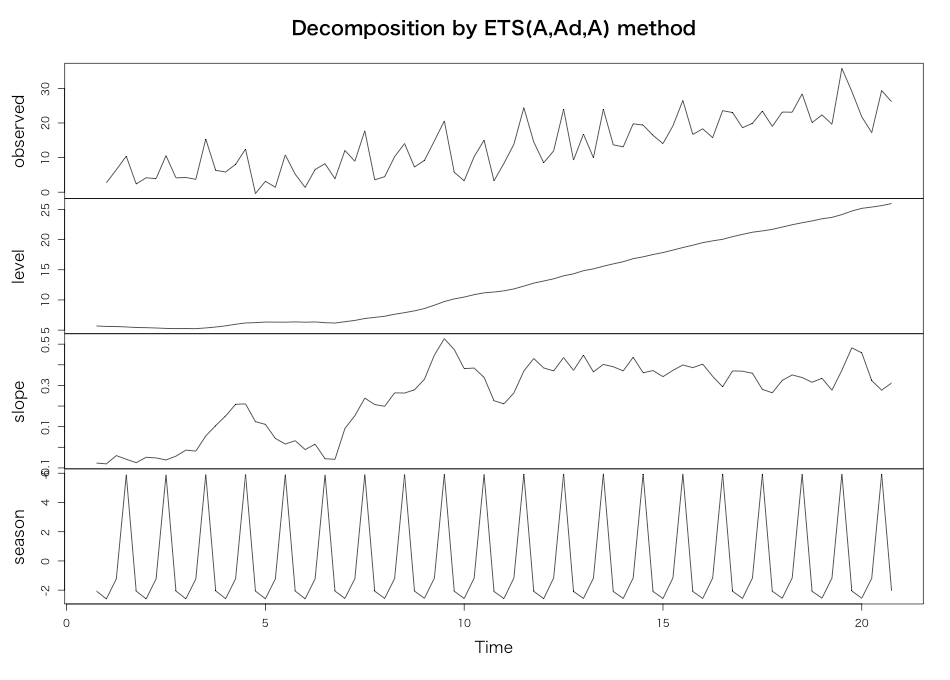
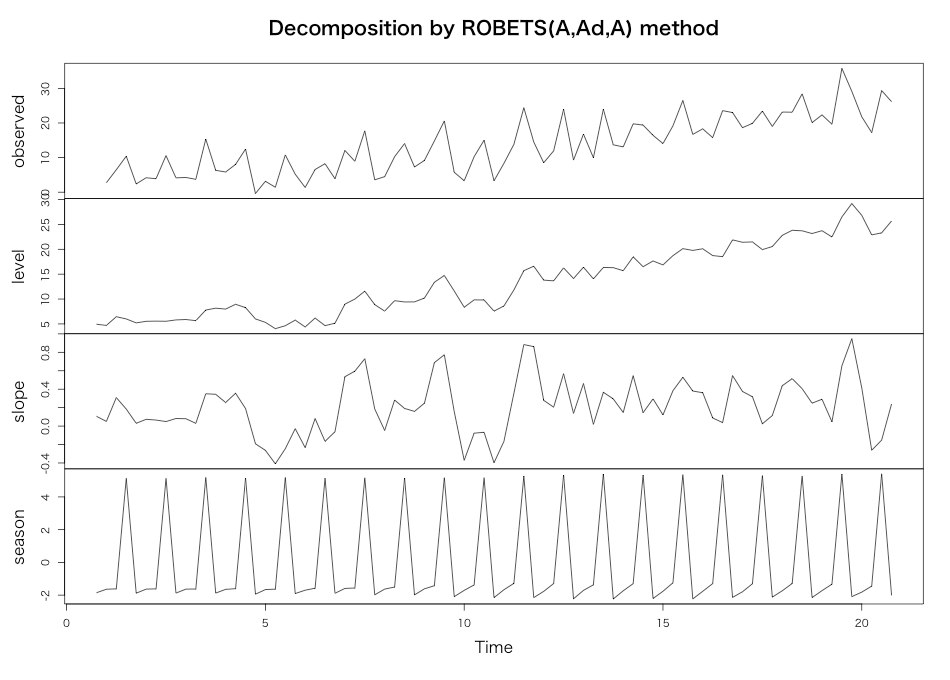
ETSに比べるとRobust ETSの方が若干ばらつきに対して鋭敏なモデルであるように見えるんですが、これって大昔*3にチラッと習ったロバスト制御なんかの「モデル自体を柔軟にして大きな外乱が入ってもモデル範囲内に収められるようにする」というのと考え方が一緒なのかなー、これはもしかしたら大昔取った杵柄で制御工学と状態空間モデル全般を復習しなきゃなー、と思ったところで勉強が追い付かなくなったのでこれにてお開きということで。。。