統計学や機械学習の世界ではよく引用される"All models are wrong; but some are useful"(全てのモデルは間違っている、だが中には役立つものもある)という格言ですが、2013年に亡くなった統計学の大家George E. P. Boxの言葉だと伝わっています。Wikipediaにも別建ての記事があって、例えば
Box repeated the aphorism in a paper that was published in the proceedings of a 1978 statistics workshop.[2] The paper contains a section entitled "All models are wrong but some are useful". The section is copied below.
Now it would be very remarkable if any system existing in the real world could be exactly represented by any simple model. However, cunningly chosen parsimonious models often do provide remarkably useful approximations. For example, the law PV = RT relating pressure P, volume V and temperature T of an "ideal" gas via a constant R is not exactly true for any real gas, but it frequently provides a useful approximation and furthermore its structure is informative since it springs from a physical view of the behavior of gas molecules.
For such a model there is no need to ask the question "Is the model true?". If "truth" is to be the "whole truth" the answer must be "No". The only question of interest is "Is the model illuminating and useful?".
というようにどの文献でどのような文脈で語られたかが記されています。個人的にはこの理想気体の状態方程式の例はなかなかに分かりやすいなと思った次第です。
しかしながら、現実にモデリングを行った上でモデルの選定という場面になった時に例えば「もっと精度の高いモデルでないとダメだ」みたいな意見が(特に非研究・非開発部門の人々の口から)出ることが少なからずあり、それが足かせになるケースもあるようです。
単に学習データへの精度が高いモデルばかり嗜好することの危険性は、過去のブログ記事でも何度か汎化性能がいかに大事かという論の一環として取り上げたことがあります。
ところが汎化性能の問題も理解した上で、それでもなお「とにかくモデルとしてはもっと交差検証精度の高いモデルでないとまかりならん」みたいな高精度至上主義みたいな要求が出る現場も世の中にはあると時々聞きます。
気持ちはもちろん分からないでもありません。何故なら統計分析にせよ機械学習システムにせよ、モデルというのはできれば高精度であるべきで予測精度にも優れている方がありとあらゆる面で有利だからです(ズバリinferenceする場合でも単にreasoningする場合でも)。概して、特に非専門家になるほど「(学習データへの)精度99%」「交差検証精度93.5%」と言った誰でも理解できる単純なbig numberに囚われがちです。
一方で、モデリングの実務の現場はそんなに単純なものではありません。ケースバイケースですが場合によってはそれ以上モデルの精度を上げようとするとコストも時間もかかって割に合わない。。。ということもあります。そういう時にいかにしてモデリングを行うべきかというのは、現場でモデリングを担当する身としては悩ましい問題です。そこで、そういう時に何を意識すれば良いのかを以下にちょっとだけ考察してみます。
そうそう、いつもながらですが僕が思いつきで書いてみただけの論なので間違いなどが多数ある可能性があります。お気付きの方はどしどしコメントなどでツッコミをいただけると有難いですm(_ _)m
精度の面で劣ったり原理的には正確ではないが、「役立つ」モデルの例
あまり適切ではないかもしれませんが、こんな例を考えてみます(これはおかしいぞ!というところがあったらバシバシ突っ込んで下さると有難いです)。適当な二値分類のデータを想定します。
> # Set data & parameters > set.seed(71) > x1 <- runif(1000, 1, 5) > set.seed(72) > x2 <- runif(1000, -2, 2) > set.seed(73) > x3 <- runif(1000, 10, 12) > set.seed(74) > x4 <- runif(1000, 0, 1) > b0 <- 17 > b1 <- 1 > b2 <- 3 > b3 <- -1.9 > b4 <- 2 > set.seed(101) > q <- b0 + b1*x1 + b2*x2 + b3*x3 + b4*x4 + rnorm(1000, 0, 3) > y <- plogis(q) > y1 <- round(y, 0)
見ての通り、目的変数そのものはx1, x2, x3, x4の4つの説明変数から生成されたものです。が、ここでちょっと見方を変えてみます。x4についてのみ、まず四捨五入して0 or 1の二値に直した新たな説明変数x5を用意します。その上で3:1の比率で学習vs.テストデータセットに分けて、学習データをロジスティック回帰した上でテストデータへの予測精度を見てみます。
> set.seed(75) > idx <- sample(1000, 250, replace=F) # 元の説明変数から成るデータセット > d1 <- data.frame(y=y1, x1=x1, x2=x2, x3=x3, x4=x4) > d1_train <- d1[-idx,] > d1_test <- d1[idx,] # x4を四捨五入したものに差し替えたデータセット > x5 <- round(x4, 0) > d2 <- data.frame(y=y1, x1=x1, x2=x2, x3=x3, x4=x5) > d2_train <- d2[-idx,] > d2_test <- d2[idx,] > d1_train.glm <- glm(as.factor(y)~., d1_train, family=binomial) > d2_train.glm <- glm(as.factor(y)~., d2_train, family=binomial) > summary(d1_train.glm) Call: glm(formula = as.factor(y) ~ ., family = binomial, data = d1_train) Deviance Residuals: Min 1Q Median 3Q Max -2.5900 -0.5091 0.1507 0.5462 2.6931 Coefficients: Estimate Std. Error z value Pr(>|z|) (Intercept) 6.5742 1.9883 3.306 0.000945 *** x1 0.7458 0.1037 7.191 6.45e-13 *** x2 1.9285 0.1329 14.509 < 2e-16 *** x3 -0.8628 0.1845 -4.676 2.92e-06 *** x4 1.4591 0.3672 3.973 7.09e-05 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 (Dispersion parameter for binomial family taken to be 1) Null deviance: 1037.59 on 749 degrees of freedom Residual deviance: 565.56 on 745 degrees of freedom AIC: 575.56 Number of Fisher Scoring iterations: 5 > summary(d2_train.glm) Call: glm(formula = as.factor(y) ~ ., family = binomial, data = d2_train) Deviance Residuals: Min 1Q Median 3Q Max -2.5469 -0.5281 0.1475 0.5552 2.8000 Coefficients: Estimate Std. Error z value Pr(>|z|) (Intercept) 6.7283 1.9938 3.375 0.000739 *** x1 0.7505 0.1039 7.221 5.16e-13 *** x2 1.9548 0.1347 14.507 < 2e-16 *** x3 -0.8536 0.1843 -4.632 3.63e-06 *** x4 0.9302 0.2203 4.222 2.43e-05 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 (Dispersion parameter for binomial family taken to be 1) Null deviance: 1037.59 on 749 degrees of freedom Residual deviance: 563.29 on 745 degrees of freedom AIC: 573.29 Number of Fisher Scoring iterations: 5 > table(d1_test$y, round(predict(d1_train.glm, newdata=d1_test, type='response'))) 0 1 0 99 16 1 22 113 > sum(diag(table(d1_test$y, round(predict(d1_train.glm, newdata=d1_test, type='response')))))/250 [1] 0.848 > table(d2_test$y, round(predict(d2_train.glm, newdata=d2_test, type='response'))) 0 1 0 99 16 1 20 115 > sum(diag(table(d2_test$y, round(predict(d2_train.glm, newdata=d2_test, type='response')))))/250 [1] 0.856
面白いことに、x4を四捨五入して簡単にした説明変数x5を使ったデータセットの方が、交差検証精度が高くなっています。そこで、もっと極端なものを考えてみましょう。今度はx1-x3の残りの説明変数についても、[0, 1]の区間に正規化した上でさらに四捨五入して完全に二値に変えたものに差し替えてみます。
> xx1 <- round((x1 - min(x1)) / (max(x1) - min(x1)), 0) > xx2 <- round((x2 - min(x2)) / (max(x2) - min(x2)), 0) > xx3 <- round((x3 - min(x3)) / (max(x3) - min(x3)), 0) > d3 <- data.frame(y=y1, x1=xx1, x2=xx2, x3=xx3, x4=x5) > d3_train <- d3[-idx,] > d3_test <- d3[idx,] > d3_train.glm <- glm(as.factor(y)~., d3_train, family=binomial) > summary(d3_train.glm) Call: glm(formula = as.factor(y) ~ ., family = binomial, data = d3_train) Deviance Residuals: Min 1Q Median 3Q Max -2.4244 -0.6906 0.3298 0.6230 2.3338 Coefficients: Estimate Std. Error z value Pr(>|z|) (Intercept) -2.0326 0.2332 -8.716 < 2e-16 *** x1 1.1271 0.2026 5.563 2.64e-08 *** x2 3.0695 0.2085 14.721 < 2e-16 *** x3 -0.6229 0.1915 -3.252 0.001145 ** x4 0.7205 0.1918 3.756 0.000173 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 (Dispersion parameter for binomial family taken to be 1) Null deviance: 1037.59 on 749 degrees of freedom Residual deviance: 703.46 on 745 degrees of freedom AIC: 713.46 Number of Fisher Scoring iterations: 4 > table(d3_test$y, round(predict(d3_train.glm, newdata=d3_test, type='response'), 0)) 0 1 0 96 19 1 26 109 > sum(diag(table(d3_test$y, round(predict(d3_train.glm, newdata=d3_test, type='response'), 0))))/250 [1] 0.82
結構大胆な変数の変換をしたと思うのですが、実際にはそれほど大きく精度は下がっていません。しかもreasoningに用いるという観点だけから言えば、大小関係も正負の符号も合っているので、これでも十分に実用に耐えそうです。データを取ってくる手間などを考えたら、場合によってはこの「全ての説明変数が何かの基準に基づいて勝手に記録された二値のダミー変数」だけで出来たモデルの方がコストも時間もかからなくてずっと便利だということになる可能性もあるはずです。
その意味で言えば、3番目の極端に怠惰なやり方をしたモデルであっても"useful"と言っても差し支えないのでしょう。決して元のデータの生成過程に沿っているわけではないモデルであっても、実用上は役立つこともあるというわけです。
似たような話は以前にもしたことがあります。「ロジスティック回帰のある領域に限れば線形回帰でも十分に使える」というお話です。
ローカルマシンで回せるような規模のデータならどちらであっても差し支えないと思いますが、これが分散処理をしてでも回さなければならないような大規模データの話になると勝手はだいぶ変わってきます。できれば最尤推定が必要なロジスティック回帰より、最小二乗法で簡単に済む線形回帰の方が楽で良いみたいなケースも実務だとチラホラあるというのが個人的な認識で、そういう時には線形回帰で済ませてもいいんじゃない?というのを確かめに行ったのが上記の記事でした。
だがシンプソンのパラドックスにも気をつける必要がある
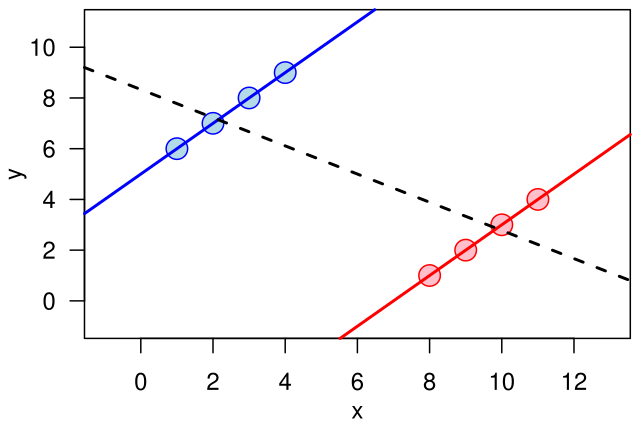
一方で、要らないものを切り捨てて実用に適したシンプルなモデルにたどり着くことができたと思っても安心してはいけないと個人的には思っています。何故なら、この地上には「シンプソンのパラドックス」という、モデリングにおいて過学習と並ぶ最大の落とし穴があるからです。
うまいこと余計なものを切り落として分かりやすく実用的なモデルが出来たと思ったら、実はデータ全体の一部をうまく説明できるモデルが出来ただけだった、データ全体に対して適用してみたら大嘘というとんでもないモデルだった。。。ということになる危険性もあるわけです。そのようなモデルをreasoningのために用いて意思決定したり、はたまたinferenceに用いたりすれば、間違った結果になる可能性があることは否めません。
実際、前述の「ロジスティック回帰の一部を線形回帰で代用する」件もよくよく考えてみれば「単にやってくる〇〇率のデータが正規分布する領域のものに限られているからそれでうまくいっているに過ぎない」ということなんですよね。将来的に端っこの領域のデータが来るようになったら当てはまらなくなるということを考えれば、これも(悪く言えば)シンプソンのパラドックスの一つなのかなと思っています。
モデルはあくまでも「目の前の森羅万象の或る一つの切り口」に過ぎない
良い喩えがないかなと考えていて、ふと思い出したのが「円錐曲線」です。
これは実際には遥かに厳密な数学の上に成り立っている話なので、数学が大の苦手な僕ごときが知ったかぶりの出来る話ではありません(汗)。しかしながら「実際には1組の円錐であってもその切り口によって多彩な曲線が現れてしまう=いずれもが円錐のある一面を表しているがそのひとつひとつだけ見ても円錐全体のことは分からない」と僕には読めました。
Wikipedia記事にもあるように、円錐曲線の理論はアポロニウス・パスカル・オイラーによって体系化されたとのことですが、言い換えるとこれらの二次曲線を見てひとつの円錐の切り口として捉えられるはずだと突き止められたのは彼らのような天才だったからでしょう。同じことを「目の前のモデル」と「この地上の森羅万象の背後にある潜在的な究極のモデル」との関係に置き換えれば、彼らのような天才か神でもない限りは、前者から後者にたどり着くのはほぼ不可能ではないかと思われます。
そのように考えると、究極のところ天才でもなければ況してや神ならざる身としては、「目の前の森羅万象の或る一つの切り口」を可能な限り広く探し回り、その上で「目の前の課題に最も役立つ切り口を見出す」ことが最も大切なのかな、とふと考えた次第です。