この記事は、遥か昔のこちらの記事の続きのようなものです。また何度も何度も恐縮ですが、今回の記事内容も付け焼き刃で書いているので色々間違っている可能性があります。お気付きの方は是非ご指摘くださいm(_ _)m
各方面のエコノメトリシャンの方々と上記記事を書いた際に議論*1したことがあるのですが、その時は基本的に統計モデリングを行う際は以下のような判別表に従ってモデルを使い分けるべきだという話になったのでした。
| 確率分布 | 特徴 |
|---|---|
| ポアソン分布 | データが正の離散値、平均値30ぐらいまで、標本平均=標本分散 |
| 負の二項分布 | データが正の離散値、平均値30ぐらいまで、標本平均<標本分散 |
| 二項分布 | データが離散値、ゼロ以上でしかも有限 (0, 1, 2, ... N) |
| 正規分布 | データが連続値もしくは離散値でも平均値が十分大*2 (-∞~∞) |
| 対数正規分布 | 同上、ただし正の値、範囲 (0~∞) |
| ガンマ分布 | データが連続値、範囲 (0~∞) |
ところが、現実にはこの判別表に従うとかえってモデリングの精度が悪くなるケースというのが実データを相手にしていると割と頻繁にあって、意外と判断に迷うことが多いんですね。端的に言うと「○○『率』のように明らかにロジスティック回帰の方が当てはまりが良さそうなものであっても、データの取得状況によっては目的変数が正規分布しているように見えて、実際に線形回帰するとR^2でも交差検証(CV)でも精度が同等もしくは優れている場合はどうするべきか」というような話です。
特に「単純にreasoning / interpretationが目的なので推定パラメータ(偏回帰係数)の大小や符号が分かればOK」という場面でどうかとなると、結構悩ましいところです。その場合は確かに線形回帰してもそれなりの結果になることが経験上見込めるからです。加えて線形回帰の方が当然ながら計算負荷も軽いので、それなりの結果になるなら線形回帰すればええやんという話になるのは想像に難くありません。
モデル精度原理主義的には「そんなのCV精度の高い方を選べばええやん」でおしまいだという気もするんですが、それでもデータの生成過程が明確に見えている状況であえて線形回帰にしてもいいんだっけ?というのが個人的にあるので、とりあえずシミュレーションデータでチェックしてみようと思います。
シミュレーションデータで試してみる
ベタッとRで書いてみます。ちなみに、多分これでロジスティック回帰のシミュレーションデータの作り方は合ってると思うんですが。。。間違っていたら悲しいので、おかしなところを見つけた方是非容赦無くご指摘くださいm(_ _)m
# 説明変数 > set.seed(71) > x1 <- runif(5000, 0, 1) > set.seed(72) > x2 <- runif(5000, 0, 1) > set.seed(73) > x3 <- runif(5000, 0, 1) > set.seed(74) > x4 <- runif(5000, 0, 1) > set.seed(75) > err <- rnorm(5000, 0, 1) # 真の偏回帰係数 > b1 <- 6 > b2 <- 3 > b3 <- -3 > b4 <- -6 # 回帰子 > p <- b1*x1 + b2*x2 + b3*x3 + b4*x4 + err # ロジット変換 > y <- plogis(p) > plot(p, y) # データフレームにする > d <- data.frame(y=y, x1=x1, x2=x2, x3=x3, x4=x4)
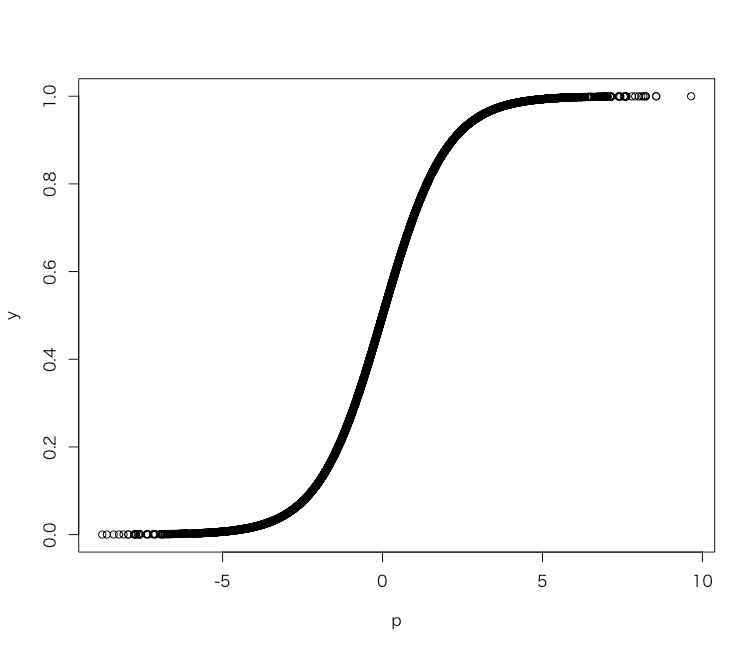
シミュレーションデータはこれで生成できました。試しに普通にロジスティック回帰してみます。
> d.glm <- glm(y~., d, family=binomial) 警告メッセージ: eval(family$initialize) で: 二項 glm で整数でない成功数がありました! > summary(d.glm) Call: glm(formula = y ~ ., family = binomial, data = d) Deviance Residuals: Min 1Q Median 3Q Max -1.5287 -0.1925 0.0006 0.1918 1.4651 Coefficients: Estimate Std. Error z value Pr(>|z|) (Intercept) -0.09489 0.13048 -0.727 0.467 x1 5.19189 0.17355 29.916 <2e-16 *** x2 2.63917 0.14396 18.333 <2e-16 *** x3 -2.47161 0.14389 -17.177 <2e-16 *** x4 -5.15022 0.16935 -30.412 <2e-16 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 (Dispersion parameter for binomial family taken to be 1) Null deviance: 3283.97 on 4999 degrees of freedom Residual deviance: 522.16 on 4995 degrees of freedom AIC: 2914.6 Number of Fisher Scoring iterations: 6
各パラメータを見てみると普通に生成した時の係数に近い結果になりました。次に、区間[0.4, 0.6]でデータを切り取って、これをそれぞれロジスティック回帰と線形回帰してみます。
# 上記区間だけ抜き出す > d2 <- d[d$y>=0.4&d$y<=0.6,] # ロジスティック回帰 > d2.glm <- glm(y~., d2, family=binomial) 警告メッセージ: eval(family$initialize) で: 二項 glm で整数でない成功数がありました! > summary(d2.glm) Call: glm(formula = y ~ ., family = binomial, data = d2) Deviance Residuals: Min 1Q Median 3Q Max -0.258996 -0.096203 0.002195 0.094381 0.219714 Coefficients: Estimate Std. Error z value Pr(>|z|) (Intercept) -0.03648 0.29660 -0.123 0.902 x1 0.35723 0.58223 0.614 0.540 x2 0.20728 0.38355 0.540 0.589 x3 -0.15676 0.38059 -0.412 0.680 x4 -0.32663 0.58364 -0.560 0.576 (Dispersion parameter for binomial family taken to be 1) Null deviance: 7.7568 on 552 degrees of freedom Residual deviance: 7.3232 on 548 degrees of freedom AIC: 770.57 Number of Fisher Scoring iterations: 3 # 線形回帰 > d2.lm <- lm(y~., d2) > summary(d2.lm) Call: lm(formula = y ~ ., data = d2) Residuals: Min 1Q Median 3Q Max -0.129281 -0.048069 0.001069 0.047073 0.109597 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 0.49089 0.00855 57.414 < 2e-16 *** x1 0.08924 0.01677 5.320 1.51e-07 *** x2 0.05178 0.01105 4.686 3.52e-06 *** x3 -0.03916 0.01097 -3.570 0.000388 *** x4 -0.08160 0.01682 -4.852 1.59e-06 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 0.05768 on 548 degrees of freedom Multiple R-squared: 0.05611, Adjusted R-squared: 0.04922 F-statistic: 8.145 on 4 and 548 DF, p-value: 2.199e-06
パラメータの大きさ自体は合っていませんが、符号と比だけ見ると線形回帰でもそれなりに元のパラメータ同士の関係性を表していることが分かります。そこで、ここだけ拡大して元データ・ロジスティック回帰での再当てはめ結果・線形回帰での再当てはめ結果の3つを比べてみます。
# 上記区間のx軸の値を取得する > p2 <- p[as.integer(row.names(d2))] # 重ね合わせてプロットしてみる > matplot(p2, cbind(d2$y, predict(d2.glm, newdata=d2, type='response'), predict(d2.lm, newdata=d2)), pch=c(19,19,1), cex=c(1,1,3), xlab='', ylab='') # 相関係数だけざっくり見る > cor(predict(d2.glm, newdata=d2, type='response'), predict(d2.lm, newdata=d2)) [1] 0.9999998
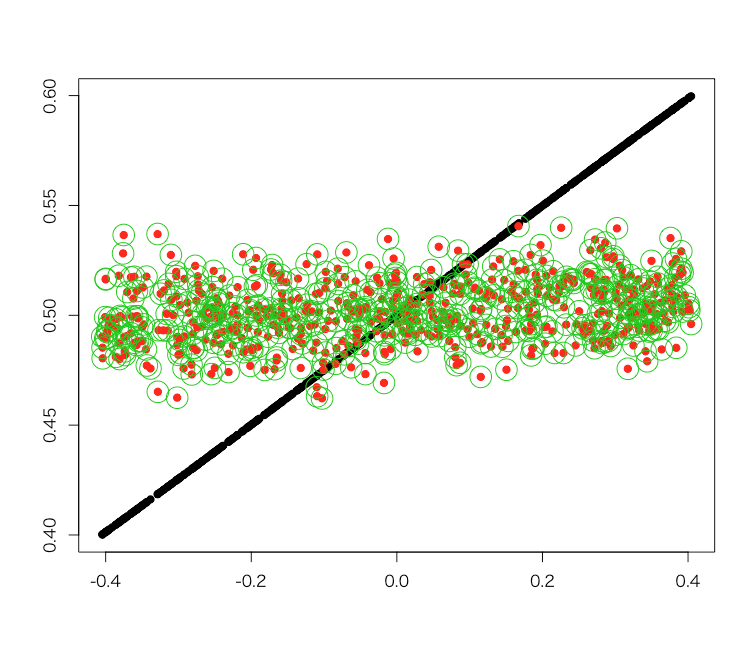
この区間だけで見ると、嫌な言い方ですが「ロジスティック回帰でも線形回帰でも等しく当てはまりが悪い」ことが分かります。一方で、ロジスティック回帰と線形回帰双方の再当てはめ結果はほぼ一致することが分かります。この領域ではどちらで計算しても同じようなモデルになりそうです。
一方、線形回帰を全領域でやるとこうなります。
> d.lm <- lm(y~., d) > summary(d.lm) Call: lm(formula = y ~ ., data = d) Residuals: Min 1Q Median 3Q Max -0.5482 -0.1174 -0.0018 0.1195 0.5076 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 0.489555 0.008282 59.11 <2e-16 *** x1 0.727627 0.008112 89.70 <2e-16 *** x2 0.358074 0.008007 44.72 <2e-16 *** x3 -0.333494 0.008069 -41.33 <2e-16 *** x4 -0.731140 0.007930 -92.20 <2e-16 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 0.164 on 4995 degrees of freedom Multiple R-squared: 0.7991, Adjusted R-squared: 0.7989 F-statistic: 4967 on 4 and 4995 DF, p-value: < 2.2e-16
本来の偏回帰係数とは似ても似つかないパラメータの推定結果になりました。ただし「符号と比」についてはやはり狭い区間の時と同様に真の偏回帰係数の関係が保たれているようです。そこで、これをやはり同様に全区間で再当てはめして比べてみましょう。
# 重ね合わせてプロットしてみる > matplot(p, cbind(d$y, predict(d.glm, newdata=d, type='response'), predict(d.lm, newdata=d)), pch=c(19,19,1), cex=c(2,1,1), xlab='', ylab='') # ざっくり相関係数を見てみる > cor(d$y, predict(d.glm, newdata=d, type='response')) [1] 0.9268167 > cor(d$y, predict(d.lm, newdata=d)) [1] 0.8939221 > cor(predict(d.glm, newdata=d, type='response'), predict(d.lm, newdata=d)) [1] 0.9627183

当たり前ですが、本来の定義域が[0, 1]なのでロジスティック回帰で再当てはめすると綺麗に元データに沿うように収まるものの、線形回帰で再当てはめすると物の見事に上下に飛び出してしまいます。相関係数のようなざっくりとした指標だと分かりづらいですが、プロットで見比べると一目瞭然です。
ということである意味予想された結果ながら、「厳密に偏回帰係数を求めようと思ったらロジスティック回帰でなければいけない」ものの「単純にreasoning / interpretationのためにパラメータの大小や比だけ分かれば良い状況なら線形回帰で代用しても(場合によっては)差し支えない」ということが分かりました。
おそらく最も妥当と思われる説明
生起確率pとして、被説明変数をp、p/(1-p)、log(p/(1-p))のどれにしてOLSがよく当てはまるのかが気になりますが、たぶん上手くテイラー展開したら、p=0.5周辺で線形近似になることを示せるのではないかと。 https://t.co/IJBjK9T0V2
— uncorrelated (@uncorrelated) 2017年12月7日
以前よくお世話になっていたアンコレこと@uncorrelatedさんから、ズバリこのようなコメントをいただきました。これ考えてみたら当たり前で、GLMであればロジスティック回帰に限らず、テイラー展開した際に一次の項までで十分に近似できてしまうようなサンプルに対しては、事実上線形回帰で表せるわけです*3。そりゃそういうケースでは線形回帰(≒一次の項)であってもR^2見ようがCV誤差見ようが精度はそれなりになるよな、と。。。
感想
そのうち別の記事でだらだら書こうかと思っていますが、実務の現場だと原理主義的にベストのモデルを選択するよりも「とりあえず目の前の課題に適したモデルでクイックに結果を出すべき」というシチュエーションが少なくありません。今回は「GLMであるべきものを線形回帰で代用しても問題ないかどうか」というポイントに絞ってみましたが、その他のケースでも同じような結論に至るものが実は結構あるのかな?と思った次第です。
追記
上記のシミュレーションですが、明らかにロジスティック分布の「ノイズなし」バージョンになっていてこれだと幾ら何でもひどくないか的な雰囲気があり。。。どなたかベストのシミュレーション生成方法をご存知でしたら是非ご教示くださいm(_ _)m
追記2
上にもあるように、
上記のシミュレーションですが、明らかにロジスティック分布の「ノイズなし」バージョンになっていてこれだと幾ら何でもひどくないか的な雰囲気があり。。。
とずっと思っていて、これは何か変だなという違和感を抱えたままでずっと来ていたのでした。
この点について、id:ill-identifiedさんが最近話題になった別の件に絡めて非常に分かりやすい記事をまとめてくださっています。
端的に言えば、以下の下りが本質の全てを表しています。
ロジスティック回帰はまず, 説明変数
とパラメータ
をつかって,
という量
を作る.
は
の範囲を取るので, 次に冒頭のロジスティック曲線を使って, ゼロ以上1以下の値につぶした値
を作る.
は必ずゼロから1の範囲を取るので, これは確率とみなせる. 何の確率かというと, 目的変数が 1 (今回の図では TRUE に対応する) になる確率である. そこで, 以下のように条件で分岐させることで, 目的変数の予測値を出力できる.
よって,
に対して予測値の決まる境界線は,
の場合から逆算すると,
という一次式で表される.
はロジット関数という, ロジスティック曲線の逆関数で,
である. 明らかにロジスティック曲線ではなく, 直線である. SVM などと同じ, 線形分類モデルと呼ばれるタイプの学習アルゴリズムである.
つまり「ロジスティック回帰が引く線はロジスティック曲線ではなく直線であるはずだ」というのがここでの最重要なポイントです。「分類」については式を見る限りではこの解釈が正しいと僕も思いました。このブログでやってしまったように最初から「ロジスティック曲線」そのものを回帰モデルの形状として使おうとするのは誤った解釈だというわけです。
一方で今回話題にしているのは分母と分子から定義される「率」の話題なので、これはどうしようかなと。理屈の上では明らかに「分類」の時と同様に直線が引けるわけですが、直接「分類確率」を相手にすると考えるとモデルを推定してから一度ロジットを逆変換してpに戻すということになるので、やっぱりロジスティック曲線になってしまう……? ちょっと考えてみます。
追記3
考えてみたら当たり前なんですが、整理すると
- 「分類」なら0 or 1に帰着させる必要があるので、線を引いて上下に分けるということを考えることになる。これはid:ill-identifiedさんの記事で指摘されたように、ロジット変換後の空間で直線を引いて上下に分けるのが正しい
- 「回帰」なら連続値として得られた目的変数に対して、モデリングに使う関数の誤差が最小化するように「線」を引くことになる。もし目的変数が生の「分類確率」でこれに対して「回帰」するのであれば、それは目的変数の分布に従った線を引く必要がある
- この場合目的変数がロジスティック曲線に沿うように0付近 & 1付近に多く分布するのであればロジスティック回帰のままで良いが、そうでなければ便宜的に目的変数が従う分布に沿ったモデル形状を選択することになる
- ただし、定義域[0, 1]という制約条件をつけたモデルになるのでどれを選んでも(一般的には)単なる近似解となる。厳密には定義域[0, 1]でなおかつ任意の形状の分布に従う変数を表現可能な別の分布を考えて、それに基づくGLMとしなければいけない
- 損失関数に何を選ぶかによっても変わってくると考えられる(当たり前だがOLS誤差だったら線形回帰だし、そうでないならそれなりのGLMになる)
ということなんですね。思っていたよりも面倒な話になってきた気がします。。。どなたか詳しい方ご教授くださいm(_ _)m
追記4
@shunji_umetani先生が以下のように連続ツイートなさっていたので、ママ引用いたします。
与えられたデータに対してモデルやアルゴリズムを自動的に選択する枠組みは、よほど上手く研究テーマを設定しないと、一段階メタなレベルで考えて見たけど、問題を棚上げしただけになってしまって理論的に何も言えなかったとなりそうで手がつけ難いんだろうと思う。
— Umepon (@shunji_umetani) 2018年5月24日
例えば、アルゴリズムの自動選択やりたいと言うと、ノーフリーランチ定理あるよね?というツッコミがすかさず飛んで来るわけで、研究テーマとして成立するためには、現実を上手く捉えた良い仮定が1つ2つ必要になる。
— Umepon (@shunji_umetani) 2018年5月24日
ここで「汎用性」という言葉を口にしたときに,それが「可能な任意のデータに対して等しく良い性能を実現する」ことを意味しているか?を考えるべきで,たぶん,本当にやりたいのは「現実的にありえるデータに対しておおよそ良い性能を実現する」ことなんだろうと思う.
— Umepon (@shunji_umetani) 2018年5月24日
「現実的にありえるデータ」をどのように数学的に簡潔に特徴付けるかが最も重要でかつ難しいことなんだろうなと.そういう意味では,compressive sensing は非常に上手い仮定をおいた例として挙げられると思う.
— Umepon (@shunji_umetani) 2018年5月24日
個人的には,実用的な枠組みが先行して,色々な試行錯誤する中から理論的な枠組みを立ち上げるための良いヒントが生まれれば良いなあと思う.
— Umepon (@shunji_umetani) 2018年5月24日
追記5
ところで、本来の目的だった「率」の回帰について@nekomata224さんから仔細なアドバイスをいただきましたので、それに倣ってやってみたRコードを以下に書いておきます。
> set.seed(71) > x1 <- runif(5000, 0, 1) > set.seed(72) > x2 <- runif(5000, 0, 1) > set.seed(73) > x3 <- runif(5000, 0, 1) > set.seed(74) > x4 <- runif(5000, 0, 1) > # 真の偏回帰係数 > b1 <- 6 > b2 <- 3 > b3 <- -3 > b4 <- -6 > # 回帰子 > p <- b1*x1 + b2*x2 + b3*x3 + b4*x4 > pos <- rbinom(5000, 100, plogis(p+rnorm(5000))) > rate <- pos / 100 > d1 <- data.frame(pos=pos, x1=x1, x2=x2, x3=x3, x4=x4) > d2 <- data.frame(rate=rate, x1=x1, x2=x2, x3=x3, x4=x4) > fit.glm <- glm(cbind(pos, 100-pos) ~ x1+x2+x3+x4, data=d1, family=binomial) > fit.lm <- lm(rate ~ x1+x2+x3+x4, data=d2) > summary(fit.glm) Call: glm(formula = cbind(pos, 100 - pos) ~ x1 + x2 + x3 + x4, family = binomial, data = d1) Deviance Residuals: Min 1Q Median 3Q Max -15.3085 -2.0817 -0.0122 2.0508 13.5504 Coefficients: Estimate Std. Error z value Pr(>|z|) (Intercept) 0.03954 0.01310 3.019 0.00254 ** x1 5.24147 0.01750 299.481 < 2e-16 *** x2 2.55265 0.01439 177.374 < 2e-16 *** x3 -2.59052 0.01454 -178.160 < 2e-16 *** x4 -5.24284 0.01713 -305.973 < 2e-16 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 (Dispersion parameter for binomial family taken to be 1) Null deviance: 337343 on 4999 degrees of freedom Residual deviance: 57982 on 4995 degrees of freedom AIC: 76115 Number of Fisher Scoring iterations: 5 > summary(fit.lm) Call: lm(formula = rate ~ x1 + x2 + x3 + x4, data = d2) Residuals: Min 1Q Median 3Q Max -0.52396 -0.12335 0.00085 0.12191 0.51475 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 0.508765 0.008530 59.65 <2e-16 *** x1 0.728015 0.008355 87.14 <2e-16 *** x2 0.342841 0.008246 41.58 <2e-16 *** x3 -0.346840 0.008311 -41.73 <2e-16 *** x4 -0.738672 0.008167 -90.44 <2e-16 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 0.1689 on 4995 degrees of freedom Multiple R-squared: 0.7908, Adjusted R-squared: 0.7907 F-statistic: 4721 on 4 and 4995 DF, p-value: < 2.2e-16 > par(mfrow=c(2,1)) > hist(pos, breaks=50) > hist(rate, breaks=50) > par(mfrow=c(1,1)) > plot(p, rate) > pred.glm <- predict(fit.glm, newdata=d1, type='response') > pred.lm <- predict(fit.lm, newdata=d2) > matplot(p, cbind(rate, pred.glm, pred.lm), pch=c(1,1,1), cex=c(2,1,1), xlab='', ylab='')
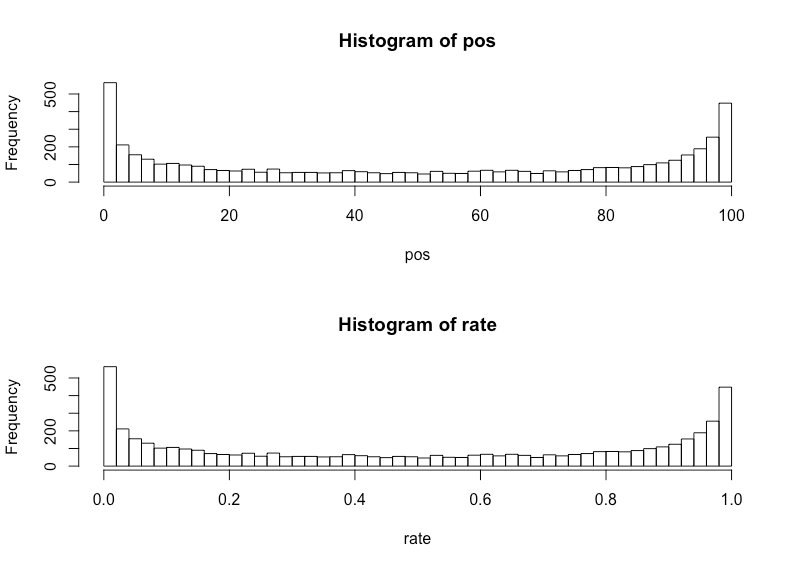
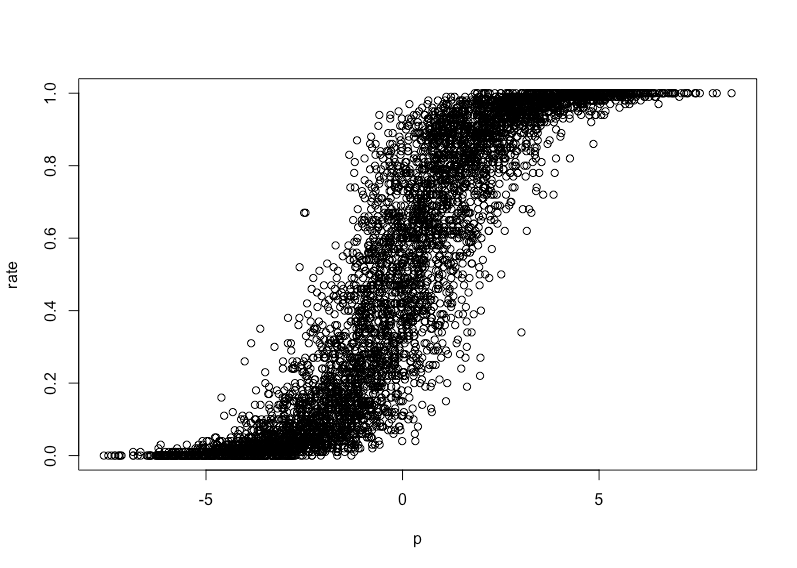
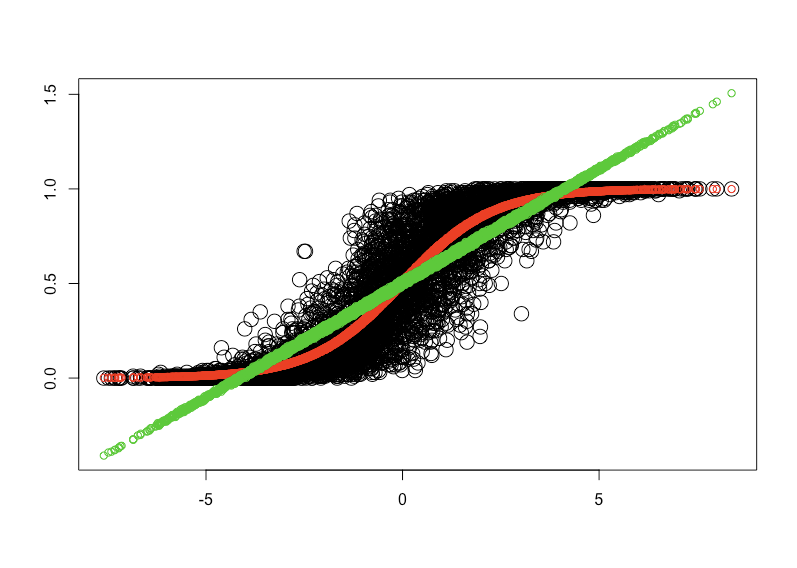
これで本来の目的は達せられたように思います。