世の中様々な介入効果・施策効果を検証するためのexperimentが行なわれていると思うんですが、意外とその効果検証というのは難しいものです。特にいわゆる統計的因果推論の立場から見れば、web上で接触する一般ユーザーに対する介入や施策といったものの検証を完全にランダム化比較試験(Randomized Controlled Trial: RCT)として実施するのは困難です。
この問題について統計的因果推論の観点からは様々なソリューションを与えることが可能なようです。例えば傾向スコア(Propensity Score)は最近色々なところで取り上げられていますし、バックドア基準といったものも挙げられます。で、今回はその中でも差分の差分法(Difference-in-Differences: DID)を取り上げることにします。理由は単純で「どうしてもexperimentによって何かしらの介入・施策の効果の有無を明らかにしたい」というケースで特に有用だと個人的には思われるからです。
おおまかな概要については、『差分の差分法』Wikipedia記事が分かりやすいかと思います。また「差の差法」という呼称になっていますが、不肖僕も刊行委員として参画している岩波DS第3巻の山口慎太郎先生の解説で取り上げられています。

- 作者: 岩波データサイエンス刊行委員会
- 出版社/メーカー: 岩波書店
- 発売日: 2016/06/10
- メディア: 単行本(ソフトカバー)
- この商品を含むブログ (3件) を見る
具体的なやり方についてはweb上の記事に良いものがいくつかあって、例えばこちらの記事は非常に分かりやすいです。
ということで、色々勉強しながらRで回すところまでやってみようかと思います。
Disclaimer
上記のreferencesしか読んでいないので、間違っているところが沢山ある可能性があります。もし間違っているところを見つけた方は、ぜひぜひツッコミを入れてくだされば幸いですm(_ _)m
差分の差分法の概要
上記のリンク先に大体のことは書いてあるのでわざわざ僕が解説するまでもないと思いますが、一応さわりのところだけちょろっと書いておきます。基本的な発想としては、カイ二乗検定に出てくるような2×2分割表タイプ実験計画をさらに拡張したものです。
一般に、2×2分割表タイプの実験計画では「介入グループvs.対照グループ」×「Yes vs. No」というまさに2×2のマトリクスになるような要因デザインを行うのが普通です。しかしながら、これだとそもそも2つのグループの間にいわゆる交絡要因があって、要因デザインだけではコントロールしきれない何かが影響する場合にはうまくいきません。岩波DS3の山口先生の解説の例だと、日本国内の2地域間で特定の自治体政策の有無の効果を調べる際に混入してくる「景気動向・社会情勢変動」といったものが挙げられます。
そこでそれらの交絡要因をコントロール可能な3つ目の軸を入れることを考えます。例えばコホート分析の手法を利用して、介入操作をある時点で行うものとしてその時点の前と後とで分ける、つまり「pre vs. post」という軸を導入します。これであれば、仮に景気動向による全体のリフトアップのような交絡要因があったとしても、対照グループでのリフトアップはあくまでも交絡要因のみに依るものであると仮定でき、さらには介入グループのリフトアップが交絡要因+介入に依るものだと仮定でき、両者のpre/post差を見ることで介入グループの方が「より大きく」リフトアップしていれば介入による影響があったとみなせる、というわけです。この概念を図示した山口先生の解説の図2をreplicateしたのが以下の図です。
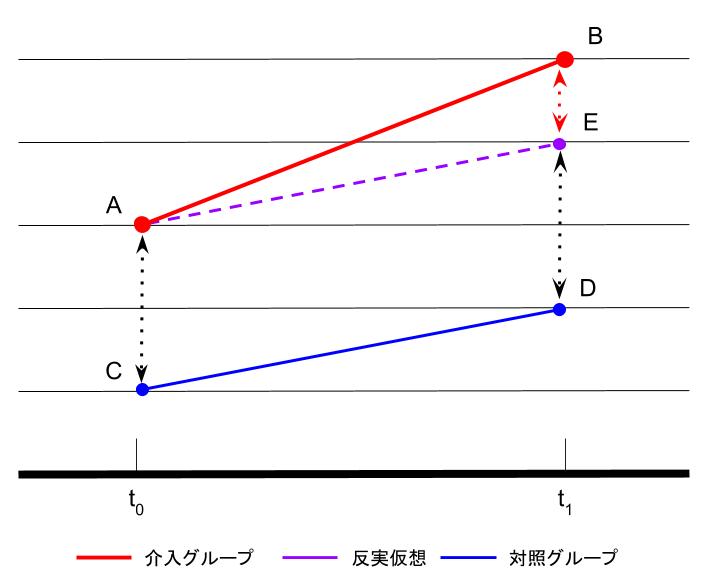
この図の説明に従えば、介入の効果は(B-A) - (D-C)で表せることが分かります。これが「差分の差分法」と呼ばれる所以です。これらを計算できるように実験計画として3軸を設定し、その上でダミー変数を設定し、後は普通に得られたデータに対して回帰分析すれば良いわけです。今回のケースだと、ダミー変数は以下のように与えれば良いことになります。最終的な差分の差分(DID)効果を示すダミー変数は介入×時期の交互作用(積)として表現されます。
| 目的変数 | 介入 | 時期 | DID |
|---|---|---|---|
| 1 | 0 | 0 | |
| 1 | 1 | 1 | |
| 0 | 0 | 0 | |
| 0 | 1 | 0 |
なお、一瞥して分かるように反実仮想(つまり介入グループに介入が行われなかったというケースを仮想した場合)である(E-A)が(D-C)と一致するという仮定がこの分析では重要であり、「平行トレンド仮定」と呼ばれます。よってこの仮定を満たすように2グループを設定する必要があるという点も実験計画面では重要なようです。また、仮にその仮定が満たせなくても何かしらの説明要因が事前に分かっている場合(例えば上記の例で言えば地域ごとの景気の差など)はこれを説明変数として盛り込むことで相殺してバランスするというやり方も考えられます。
また、個々の比較ペアごとにstudyが異なっていて介入効果のベースラインが異なるようなケースでは、studyごとにダミー変数を設定してベースラインをバランスさせるか、もしくはペアごとの個体差を変量効果として盛り込みGLMMや階層ベイズなどで全てをバランスさせた上で、モデリングすることも可能なようです。
ここまでが差分の差分法の一般的な説明で、以下Rによる実践例を書き留めていきます。今回は個人的な事情で色々拡張する必要があったので、適当なダミーデータセットを用意して3通りのパターンを想定してやってみようかと思います。
通常の「数」が対象の場合
完全にsimulated caseですが、例えば「あるEコマースサイトで新たな特典サービスを始めたので、そのサービスのプロモーションをかけてユーザー(DAU)を増やしたい」というケースを考えてみます。このサイトには幾つかサブカテゴリサイトがあり、それぞれDAUを測定しておいて、プロモーションの前後でDAUが増えたかどうかを検証するという実験を行うものと仮定します。
そこで「サブカテゴリサイトの中から8つ選んできて、うち4つについてはプロモーションを打ち、残り4つについてはプロモーションを打たない」という実験計画を組んだとしましょう。すると前者4つについては「介入あり」、後者4つについては「介入なし(対照)」と定義できます。これにプロモーションの「前」「後」とでDAU数を測定することで、DIDのモデルが組めるわけです。以下はこのサンプルデータを生成したRスクリプトです(rnormの乱数シード次第で結果は変わるので、そこは悪しからずご了承あれ)。
> d1 <- data.frame(user=round(c(rep(c(rnorm(1,10000,100),rnorm(1,10000,100)+5000,rnorm(1,20000,100),rnorm(1,20000,100)+7500),4),rep(c(rnorm(1,10000,100),rnorm(1,10000,100)+100,rnorm(1,9000,100),rnorm(1,9000,100)+100),4)),0),iv=c(rep(1,16),rep(0,16)),pr=rep(c(0,1),8)) > d1$did <- d1$iv*d1$pr > head(d1) user iv pr did 1 9973 1 0 0 2 15191 1 1 1 3 20065 1 0 0 4 27513 1 1 1 5 9973 1 0 0 6 15191 1 1 1
| user | iv | pr | did |
|---|---|---|---|
| 9973 | 1 | 0 | 0 |
| 15191 | 1 | 1 | 1 |
| 20065 | 1 | 0 | 0 |
| 27513 | 1 | 1 | 1 |
| 9973 | 1 | 0 | 0 |
| 15191 | 1 | 1 | 1 |
| 20065 | 1 | 0 | 0 |
| 27513 | 1 | 1 | 1 |
| 9973 | 1 | 0 | 0 |
| 15191 | 1 | 1 | 1 |
| 20065 | 1 | 0 | 0 |
| 27513 | 1 | 1 | 1 |
| 9973 | 1 | 0 | 0 |
| 15191 | 1 | 1 | 1 |
| 20065 | 1 | 0 | 0 |
| 27513 | 1 | 1 | 1 |
| 10028 | 0 | 0 | 0 |
| 10116 | 0 | 1 | 0 |
| 9039 | 0 | 0 | 0 |
| 9100 | 0 | 1 | 0 |
| 10028 | 0 | 0 | 0 |
| 10116 | 0 | 1 | 0 |
| 9039 | 0 | 0 | 0 |
| 9100 | 0 | 1 | 0 |
| 10028 | 0 | 0 | 0 |
| 10116 | 0 | 1 | 0 |
| 9039 | 0 | 0 | 0 |
| 9100 | 0 | 1 | 0 |
| 10028 | 0 | 0 | 0 |
| 10116 | 0 | 1 | 0 |
| 9039 | 0 | 0 | 0 |
| 9100 | 0 | 1 | 0 |
定義通り、DIDマージン効果は介入(iv)と介入前後(pr)のダミー変数の積から成るダミー変数として定義しました。このデータに対して、教科書通り線形回帰(OLS)で各要因の変回帰係数を推定すると以下のようになります。
> d1.lm <- lm(user~.,d1) > summary(d1.lm) Call: lm(formula = user ~ ., data = d1) Residuals: Min 1Q Median 3Q Max -6161 -1642 0 1642 6161 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 9533.5 1510.9 6.310 7.99e-07 *** iv 5485.5 2136.8 2.567 0.0159 * pr 74.5 2136.8 0.035 0.9724 did 6258.5 3021.9 2.071 0.0477 * --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 4274 on 28 degrees of freedom Multiple R-squared: 0.5959, Adjusted R-squared: 0.5526 F-statistic: 13.76 on 3 and 28 DF, p-value: 1.058e-05
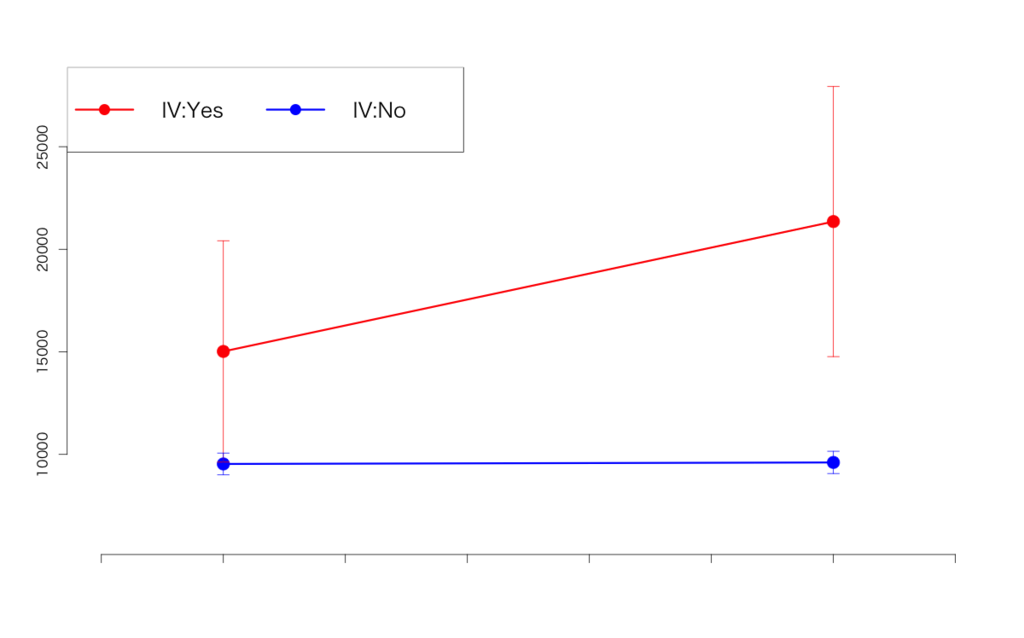
ちょっと無理のある生成データなので実際に差分の差分をプロットしてみると物凄く変な感じになっていますが(汗)、一応DIDマージン効果(did)は有意にあるという結果になっています。
「率」が対象の場合
本来ならカイ二乗検定をやる場面ですが、必ずしも2×2になるとは限らない上に「率」なので二項分布パラメータとしてみなした上でロジスティック回帰でモデリングするのが適切なようです。
今度は、上記のEコマースサイトが毎月追加料金を支払う形のプレミアム会員サービスを始めたとしましょう。そのプレミアム会員サービスのプロモーションをあるタイミングで打ったとして、そのタイミングの前後でDAUのうちどれくらいがプレミアム会員で占められるようになったかを比較することで、プロモーションの効果を検証するということを考えます。
> d2 <- data.frame(ncv=c(12000,11000,10500,11500),cv=c(1000,3000,1000,1500),iv=c(1,1,0,0),pr=c(0,1,0,1)) > d2$did <- d2$iv*d2$pr > d2 ncv cv iv pr did 1 12000 1000 1 0 0 2 11000 3000 1 1 1 3 10500 1000 0 0 0 4 11500 1500 0 1 0 > d2$cv/(d2$ncv+d2$cv) [1] 0.07692308 0.21428571 0.08695652 0.11538462
| ncv | cv | iv | pr | did |
|---|---|---|---|---|
| 12000 | 1000 | 1 | 0 | 0 |
| 11000 | 3000 | 1 | 1 | 1 |
| 10500 | 1000 | 0 | 0 | 0 |
| 11500 | 1500 | 0 | 1 | 0 |
基本的にはカイ二乗検定の2×2分割表にさらに介入「前or後」の3軸目を足して、2×2×2に変えただけです。
> d2.glm <- glm(cbind(cv,ncv)~.,d2,family=binomial) > summary(d2.glm) Call: glm(formula = cbind(cv, ncv) ~ ., family = binomial, data = d2) Deviance Residuals: [1] 0 0 0 0 Coefficients: Estimate Std. Error z value Pr(>|z|) (Intercept) -2.35138 0.03309 -71.051 < 2e-16 *** iv -0.13353 0.04668 -2.861 0.00422 ** pr 0.31449 0.04300 7.314 2.59e-13 *** did 0.87113 0.05793 15.036 < 2e-16 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 (Dispersion parameter for binomial family taken to be 1) Null deviance: 1.3573e+03 on 3 degrees of freedom Residual deviance: -1.1102e-13 on 0 degrees of freedom AIC: 43.952 Number of Fisher Scoring iterations: 2
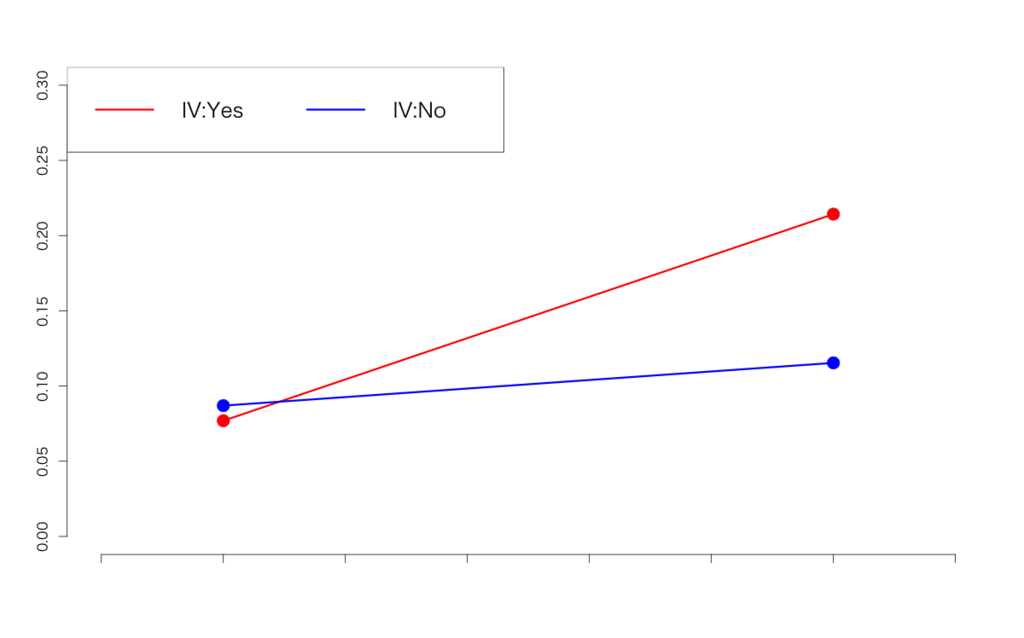
元々交互作用が極端に強いケースになっちゃったのである意味当たり前なんですが、DIDマージン効果は有意であるという結果になりました。
複数study間で「率」を対象にする場合
これはメタアナリシスなので、変量効果を考慮する必要があります。個々のstudyを分離させるだけならダミー変数を置いても良いですし、study間の差が明示的に表せないようならGLMMでも階層ベイズでもいけると思われます。データは色々simulateして以下のようにしてみました。
| ncv | cv | iv | pr | did | study |
|---|---|---|---|---|---|
| 9742 | 97 | 1 | 0 | 0 | A |
| 9436 | 159 | 1 | 1 | 1 | A |
| 9525 | 101 | 0 | 0 | 0 | A |
| 10533 | 143 | 0 | 1 | 0 | A |
| 100996 | 500 | 1 | 0 | 0 | B |
| 98293 | 607 | 1 | 1 | 1 | B |
| 102089 | 498 | 0 | 0 | 0 | B |
| 101168 | 542 | 0 | 1 | 0 | B |
| 1798 | 243 | 1 | 0 | 0 | C |
| 1901 | 308 | 1 | 1 | 1 | C |
| 1625 | 198 | 0 | 0 | 0 | C |
| 2117 | 265 | 0 | 1 | 0 | C |
> d3 ncv cv iv pr did study 1 9742 97 1 0 0 A 2 9436 159 1 1 1 A 3 9525 101 0 0 0 A 4 10533 143 0 1 0 A 5 100996 500 1 0 0 B 6 98293 607 1 1 1 B 7 102089 498 0 0 0 B 8 101168 542 0 1 0 B 9 1798 243 1 0 0 C 10 1901 308 1 1 1 C 11 1625 198 0 0 0 C 12 2117 265 0 1 0 C > d3$cv/(d3$ncv+d3$cv) [1] 0.009858725 0.016571131 0.010492416 0.013394530 0.004926303 0.006137513 0.004854416 0.005328876 [9] 0.119059285 0.139429606 0.108612178 0.111251050
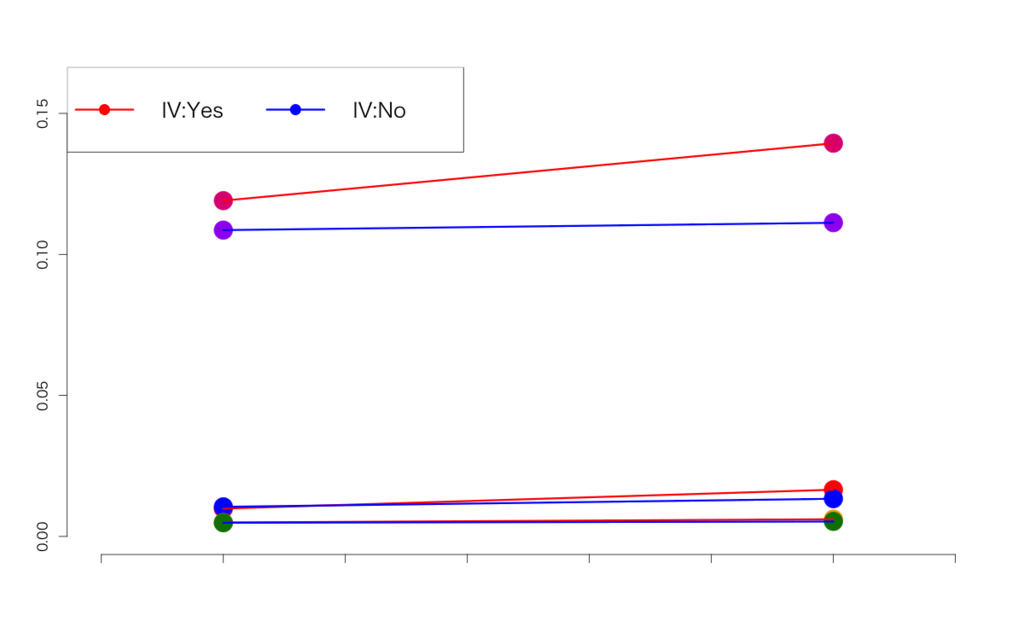
想定としては、上の「率」の例をさらに別々の商品カテゴリA, B, Cに拡張したというケースです。当然ですが、カテゴリごとにDAUの規模も違えばプロモーションがもたらすリフトアップの規模も異なります。このデータセットからプロモーションの効果があったかどうかを検証してみましょう。
個々のstudyを表すダミー変数を入れてロジスティック回帰でやる場合
これは極めて簡単で、以下の通りにやればおしまいです。
> d3.glm <- glm(cbind(cv,ncv)~., d3, family=binomial) > summary(d3.glm) Call: glm(formula = cbind(cv, ncv) ~ ., family = binomial, data = d3) Deviance Residuals: Min 1Q Median 3Q Max -1.69380 -0.70942 0.07876 0.48714 1.29887 Coefficients: Estimate Std. Error z value Pr(>|z|) (Intercept) -4.46902 0.05514 -81.047 <2e-16 *** iv 0.02763 0.05029 0.549 0.5828 pr 0.09694 0.04894 1.981 0.0476 * did 0.15543 0.06784 2.291 0.0220 * studyB -0.87043 0.04995 -17.427 <2e-16 *** studyC 2.36423 0.05611 42.133 <2e-16 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 (Dispersion parameter for binomial family taken to be 1) Null deviance: 4271.0556 on 11 degrees of freedom Residual deviance: 8.9953 on 6 degrees of freedom AIC: 108.92 Number of Fisher Scoring iterations: 4
DIDマージン効果は有意である、という結論になりました。
個々のstudy間の差を変量効果とみなして階層ベイズでやる場合
もう一つは、完全にoverkill気味ですが個々のstudy間の差を変量効果とみなして階層ベイズで片付けるというやり方。4行ずつ1つの変量効果でまとめなければいけないので、かなり汚いですが以下のようにStanスクリプトを書きます。
data {
int<lower=0> N;
int<lower=0> ncv[N];
int<lower=0> cv[N];
real<lower=0> iv[N];
real<lower=0> pr[N];
real<lower=0> did[N];
}
parameters {
real st[N/4];
real s;
real b0;
real b1;
real b2;
real b3;
}
model {
real p[N];
s~uniform(0,1e4);
st~normal(0,s);
for (i in 1:N/4){
p[4*i-3]<-inv_logit(b0+b1*iv[4*i-3]+b2*pr[4*i-3]+b3*did[4*i-3]+st[i]);
p[4*i-2]<-inv_logit(b0+b1*iv[4*i-2]+b2*pr[4*i-2]+b3*did[4*i-2]+st[i]);
p[4*i-1]<-inv_logit(b0+b1*iv[4*i-1]+b2*pr[4*i-1]+b3*did[4*i-1]+st[i]);
p[4*i]<-inv_logit(b0+b1*iv[4*i]+b2*pr[4*i]+b3*did[4*i]+st[i]);
}
for (i in 1:N){
cv[i]~binomial(ncv[i]+cv[i],p[i]);
}
}
このStanスクリプトを例えば'did_bayes.stan'という名前で保存しておいて、以下のRコードでStanサンプリングをkickさせます。「勝手にN/4なんかしてんじゃねーコノヤロー」とStanから怒られますが、一応走るはずです。
> library(rstan) > rstan_options(auto_write = TRUE) > options(mc.cores = parallel::detectCores()) > d3.dat <- list(N=nrow(d3), ncv=d3$ncv, cv=d3$cv, iv=d3$iv, pr=d3$pr, did=d3$did) > d3.fit <- stan(file='did_bayes.stan', data=d3.dat, iter=1000, chains=4) # ... # SAMPLING FOR MODEL 'did_bayes' NOW (CHAIN 1). Chain 1, Iteration: 1 / 1000 [ 0%] (Warmup) # ... # Chain 4, Iteration: 1000 / 1000 [100%] (Sampling)# # Elapsed Time: 1.91097 seconds (Warm-up) # 1.07228 seconds (Sampling) # 2.98326 seconds (Total) > d3.fit Inference for Stan model: did_bayes. 4 chains, each with iter=1000; warmup=500; thin=1; post-warmup draws per chain=500, total post-warmup draws=2000. mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat st[1] -0.28 0.19 3.27 -5.27 -1.73 -0.51 0.79 7.95 309 1.01 st[2] -1.15 0.19 3.27 -6.16 -2.61 -1.38 -0.09 7.10 309 1.01 st[3] 2.08 0.19 3.26 -2.90 0.63 1.86 3.13 10.40 309 1.01 s 5.10 0.62 6.17 1.05 1.98 3.02 5.32 25.37 101 1.05 b0 -4.19 0.19 3.27 -12.46 -5.23 -3.97 -2.73 0.80 308 1.01 b1 0.03 0.00 0.05 -0.07 0.00 0.03 0.06 0.13 435 1.01 b2 0.10 0.00 0.05 0.00 0.07 0.10 0.13 0.19 472 1.00 b3 0.15 0.00 0.07 0.02 0.11 0.15 0.20 0.29 436 1.01 lp__ -19161.19 0.23 2.65 -19167.29 -19162.79 -19160.78 -19159.19 -19157.30 136 1.03 Samples were drawn using NUTS(diag_e) at Tue Aug 2 15:05:25 2016. For each parameter, n_eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence, Rhat=1). > library(coda) > d3.fit.coda<-mcmc.list(lapply(1:ncol(d3.fit),function(x) mcmc(as.array(d3.fit)[,x,]))) > plot(d3.fit.coda[,5:8])

ベイズなので有意水準がどうたら言うのは本当は本義に悖るんですが(笑)、一応DIDマージン効果に当たる偏回帰係数b3の95%区間が0を超えている=5%有意を満たしている、というのが見て取れます。
最後に
今回は差分の差分法を取り上げましたが、統計的因果推論と言ったらやっぱり本丸は傾向スコアかなぁと。。。何だかんだで差分の差分法は観測データには使えず基本的には実験データにしか使えないわけですが、特にビジネスの現場だと観測データの方がずっと多いもので。
ということで岩波DS3を読み返しつつ、友人たちの傾向スコアに関するブログ記事も読み返しつつ、ぼちぼちやっていこうかと思います。
追記
@ibaibabaibai先生から以下のようにツッコミをいただきました。
@TJO_datasci 階層ベイズと差の差法の組み合わせって先例があるのでしょうか 文献とか教えてください
— baibai (@ibaibabaibai) 2016年8月2日
大丈夫な使い方もあると思うのですが因果推論ではバリアンスとバイアスのバランスとは普通は考えないみたいなので大分テイストが違って心配になりますよね https://t.co/Iwf7oGmwkD
— baibai (@ibaibabaibai) 2016年8月2日
確か@ibaibabaibai先生かどなたかからか、以前にも「統計的因果推論はバイアスの調整には興味があるがバリアンスの調整には関心がない」的なことを聞いたことがあって、そうなると階層ベイズのようなやり方で差分の差分法におけるバイアス=バリアンスのバランスが担保されるかというと心許ないんですよね。。。ということで、まだ今回の話は発展途上ですよというexcuseを書いておきます、すみません。