渋谷駅前で働くデータサイエンティストのブログ

元祖「六本木で働くデータサイエンティスト」です / 道玄坂→銀座→東京→六本木→渋谷駅前

一般的な時系列のモデリング＆予測に、機械学習系の手法よりも古典的な計量時系列分析の方が向いている理由を考えてみた（追記あり）

時系列分析 統計学 機械学習 R

この記事は、以下の@icoxfog417さんによる問題提起に合わせたちょっとした実験をまとめたものです。

この点について僕はこんなコメントをしたのですが。

この手の「一般的な時系列データには機械学習は向かない」論は過去何度か断片的にしてきてはいるものの、そう言えばまとめて論じたことはなかったなと思ったのでした。そこで、今回の記事では何故一般的な時系列データを機械学習で扱うのが難しいのかについて、簡単にまとめてみようと思います。


なお、いつもながらですが記事中で用いているR / Stan実装が途方も無いクソコードである点何卒ご容赦くださいm(_ _)m　加えて、理論的なポイントについてもやはり抜け漏れや理解不足などあるかと思いますので、お気付きの方はバンバンご指摘下さると有難いです（多分もっとしっかりとした確率過程の理論的背景なども踏まえた論文とかどこかにあるのではないかと思うのですが、僕には手が出ないレベルなのでここでは割愛します）。


また、僕自身はDeep Learningでもよく時系列データに対して使われるRNN系統の手法は不案内で、正直言って適切な実装が出来る自信がありませんので、今回はDeep系の手法は割愛し、代わりに枯れた理論＆実装で知られるランダムフォレストを機械学習サイドの代表例として取り上げることとしました。ただしもしかしたら以下に指摘した問題点に対してロバストに良い結果を返すRNN系統の手法があるかもしれませんので、予めお断りしておきます。

データの準備


共変量（説明変数）付きの時系列データセット"sample_marketing.csv"を僕のGitHubに用意してあるので、こちらをDLしておいてください。

想定としてはいわゆるMedia Mix Model (MMM)を模したもので、1列目に目的変数である"cv"、2列目以降に広告出稿ボリュームを表す"ad1"以下3つの説明変数が入っています。適当にプロットしてみるとこうなります。

par(mfrow = c(4, 1))
par(mar = c(1, 4, 1, 2) + 0.1)
plot(d$cv, type = 'l', lwd = 2, col = 2)
plot(d$ad1, type = 'l', lwd = 1, col = 1)
plot(d$ad2, type = 'l', lwd = 1, col = 1)
plot(d$ad3, type = 'l', lwd = 1, col = 1)

f:id:TJO:20190918125924p:plain

cvは見ているとちょっとうねった感じのトレンドと若干の周期性があるようにも見えます。一方、adは期間によっては値が入っていたり入っていなかったりするようです。


ベイジアン動的線形モデルとランダムフォレストでそれぞれモデリングして予測(forecast)してみる


この手の時系列回帰モデル（動的線形モデル）を組む際に考慮することは、基本的には以下の3パートに分けるという点です。

  1. 共変量（説明変数）による回帰パート
  2. 季節調整パート
  3. 長期トレンドパート

1つ目は言うまでもなく回帰モデルです。2つ目は24時間・7日（曜日）・12ヶ月（年）といった主にカレンダーに依存する周期変動です。そして3つ目は単位根過程やローカルレベルトレンドや二階差分トレンドなど、各時点間で関連しながら非線形に発展していくトレンドです。今回は、季節調整には7日周期成分を、トレンドには二階差分トレンドを当てはめてみることにします。つまり以下のようなモデルです。

cv_i = q_i + season_i + trend_i
q_i = \displaystyle \sum^{3}_{j = 1} \beta_j x_j, ~ q_i \sim Normal (\mu_q, s_q)
r_i = \displaystyle \sum^{7}_{j = 1} season_j + \epsilon_{r}, ~ \epsilon_r \sim Normal(0, s_r)
trend_i - trend_{i - 1} = trend_{i - 1} - trend_{i - 2} + \epsilon_{trend}, ~ \epsilon_{trend} \sim Normal(0, s_{trend})

式だけ見ていると面倒な印象がありますが、要は7日周期成分は「7日間の和が平均0＆標準偏差 s_rの正規分布に従う」、二階差分トレンドは「現時点と前の時点とのトレンド成分の差が平均0＆標準偏差 s_{trend}の正規分布に従う」、ということです。


まず、ベイジアン動的線形モデルを推定してみます。方法は幾らでもありますが、古典的な時系列モデルらしさを味わうためにあえてStanで組んでみます。StanファイルをGitHubに上げてありますが、以下からコピペしても大丈夫です。

data {
	int<lower=0> N;
	int<lower=0> M;
	matrix[N, M] X;
	real<lower=0> y[N];
}

parameters {
	real season[N];
	real trend[N];
	real s_trend;
	real s_season;
	real s_q;
	vector<lower=0>[M] beta;
}

model {
	real q[N];
	real cum_trend[N];
	for (i in 7:N)
		season[i]~normal(-season[i-1]-season[i-2]-season[i-3]-season[i-4]-season[i-5]-season[i-6],s_season);	
	for (i in 3:N)
		trend[i]~normal(2*trend[i-1]-trend[i-2],s_trend);

	cum_trend[1]=trend[1];
	for (i in 2:N)
		cum_trend[i]=cum_trend[i-1]+trend[i];
	for (i in 1:N)
		q[i]=y[i]-season[i]-cum_trend[i];
	for (i in 1:N)
		q[i]~normal(dot_product(X[i], beta),s_q);
}

これをkickするRコードもGitHubに上げてあります。ご覧になればお分かりかと思いますが、100点のデータのうち91点を学習データ＆9点をテストデータとしてholdout splitしてあります。つまり、91点でモデルを学習させて後ろの9点のcvを予測(forecast)*1させてその精度を見る、という検証のやり方です。


またこのRコードでは、同時にランダムフォレストで全く同じ学習＆テストデータに対する機械学習モデル推定＆予測を行なっています。


とりあえず以下のところまで回してみましょう。

# Data preparation

d <- read.csv('sample_marketing.csv')
d_train <- d[1:91, ]
d_test <- d[92:100, ]
dvar <- d_train[, -1]
dat <- list(N = nrow(d_train), M = ncol(dvar),
            y = d_train$cv, X = dvar)

# Time series modeling with Bayesian

library(rstan)
rstan_options(auto_write = TRUE)
options(mc.cores = parallel::detectCores())
fit <- stan(file = 'sample_marketing_holdout.stan', data = dat,
            iter = 1000, chains = 4)

# Extract samples / parameters, and estimate fitted values

slength <- 2000
fit.smp <- extract(fit)
tmp <- density(fit.smp$s_trend)
s_trend <- tmp$x[tmp$y == max(tmp$y)]
tmp <- density(fit.smp$s_season)
s_season <- tmp$x[tmp$y == max(tmp$y)]
tmp <- density(fit.smp$s_q)
s_q <- tmp$x[tmp$y == max(tmp$y)]
beta <- rep(0, ncol(dvar))
for (i in 1:ncol(dvar)) {
  tmp <- density(fit.smp$beta[(slength * (i - 1) + 1) : (slength * i)])
  beta[i] <- tmp$x[tmp$y == max(tmp$y)]
}
trend <- rep(0, nrow(dvar))
for (i in 1:nrow(dvar)) {
  tmp <- density(fit.smp$trend[, i])
  trend[i] <- tmp$x[tmp$y == max(tmp$y)]
}
season <- rep(0, nrow(dvar))
for (i in 1:nrow(dvar)) {
  tmp <- density(fit.smp$season[,i])
  season[i] <- tmp$x[tmp$y == max(tmp$y)]
}
beta_prod<-rep(0, nrow(dvar))
for (i in 1:ncol(dvar)) {
  beta_prod <- beta_prod + dvar[, i] * beta[i]
}
pred <- beta_prod + cumsum(trend) + season
matplot(cbind(d_train$cv, pred), type = 'l', lty = 1,
        lwd = c(2, 3), ylab = '', xlim = c(0, 100), ylim = c(180, 980))
legend('topleft', legend = c('Data', 'Fitted'),
       lty = 1, lwd = c(2, 3), col = c(1, 2))

# Validation

fc_dvar <- d_test[, -1]

val_trend <- rep(0, nrow(fc_dvar))
for (i in 1:2) {
  val_trend[i] <- trend[nrow(d_train) - 3 + i]
}
for (i in 3:nrow(fc_dvar)){
  val_trend[i] <- 2 * val_trend[i - 1] - val_trend[i - 2] + rnorm(1, 0, s_trend)
}

val_season <- season[(length(season) - 14 + 1):(length(season) - 14 + nrow(fc_dvar))] + rnorm(nrow(fc_dvar), 0, s_season)

fc_beta_prod <- rep(0, nrow(fc_dvar))
for (i in 1:ncol(fc_dvar)) {
  fc_beta_prod <- fc_beta_prod + fc_dvar[, i] * beta[i]
}

validate <- cumsum(trend)[nrow(d_train)] + fc_beta_prod + cumsum(val_trend) + val_season

# Machine learning: Random Forest

library(randomForest)
d_train.rf <- randomForest(cv~., d_train)
pred.rf <- predict(d_train.rf, newdata = d_train[, -1])
validate.rf <- predict(d_train.rf, newdata = d_test[, -1])

# Plotting w/o days

matplot(cbind(d_train$cv, pred, pred.rf), type = 'l', lty = 1,
        lwd = c(2, 3, 3), ylab = '', xlim = c(0, 100), ylim = c(150, 1050))
segments(91, 0, 91, 1100, lty = 3, col = 1, lwd = 2)
par(new = T)
matplot(cbind(d_test$cv, validate, validate.rf), type = 'l', lty = 1,
        col = c('blue', 'purple', '#008000'),
        lwd = c(2, 3, 3), ylab = '', xlim = c(-91, 9), ylim = c(150, 1050),
        axes = F)
legend('topleft', legend = c('Data', 'Fitted TS', 'Fitted RF',
                             'Actual', 'Forecast TS', 'Forecast RF'),
       lty = 1, lwd = rep(c(2, 3, 3), 2),
       col = c(1, 2, 3, 'purple', 'blue', '#008000'),
       ncol = 2, cex = 0.75)

f:id:TJO:20190918012058p:plain

ベイジアン動的線形モデルでは綺麗に学習データにフィットした上に予測結果もテストデータに割合良く合っているのに対して、ランダムフォレストはべったりと水平に伸びるだけの有様になってしまっています。それもそのはずで、前者は季節調整を初めから含んでいる*2のに対して、ランダムフォレストにはその情報は与えられていないからです。


ランダムフォレストに曜日の情報を与えてやり直してみる


上記の結果のままだと、ランダムフォレストに曜日の情報が与えられていないことになって不公平です。ということで、曜日を表すダミー変数を追加したデータでランダムフォレストだけやり直してみましょう。

# RF w/ days

d_day <- cbind(d, rep(c('Mon', 'Tue', 'Wed', 'Thr', 'Fri', 'Sat', 'Sun'), 15)[1:nrow(d)])
names(d_day)[5] <- 'day'
day_train <- d_day[1:91, ]
day_test <- d_day[92:100, ]
day_train.rf <- randomForest(cv~., day_train)
pred.rfday <- predict(day_train.rf, newdata = day_train[, -1])
validate.rfday <- predict(day_train.rf, newdata = day_test[, -1])

# Plotting w/ days

matplot(cbind(d_train$cv, pred, pred.rfday), type = 'l', lty = 1,
        lwd = c(2, 3, 3), ylab = '', xlim = c(0, 100), ylim = c(150, 1050))
segments(91, 0, 91, 1100, lty = 3, col = 1, lwd = 2)
par(new = T)
matplot(cbind(d_test$cv, validate, validate.rfday), type = 'l', lty = 1,
        col = c('blue', 'purple', '#008000'),
        lwd = c(2, 3, 3), ylab = '', xlim = c(-91, 9), ylim = c(150, 1050),
        axes = F)
legend('topleft', legend = c('Data', 'Fitted TS', 'Fitted RF w day',
                             'Actual', 'Forecast TS', 'Forecast RF w day'),
       lty = 1, lwd = rep(c(2, 3, 3), 2),
       col = c(1, 2, 3, 'blue', 'purple', '#008000'),
       ncol = 2, cex = 0.75)

f:id:TJO:20190918012121p:plain

確かに曜日変動＝季節調整の部分は反映されるようになりましたが、当然ながらトレンドの部分は反映されておらず*3、相変わらず平坦なフィット＆予測のままです。最後のholdout部分のforecastもベイジアン動的線形モデルに比べると少し外れ方が大きいようです。そこでRMSEを計算してみましょう。

library(Metrics)
rmse(d_test$cv, validate) # Bayesian TS
rmse(d_test$cv, validate.rf) # RF w/o days
rmse(d_test$cv, validate.rfday) # RF w/ days

乱数シード依存ではありますが、RMSEを比べてみると70.7308, 88.6625, 88.78605で、やはりベイジアン動的線形モデルが一番良いという結果になります。


機械学習系の手法は定常過程を前提としていて、非定常過程に弱い


では、何故こんなことになるのでしょうか？　例えば、オリジナルデータをholdout splitする前の目的変数cvの前半50点と後半50点を見比べるとこうなっています。

hist(d$cv[1:50], col = 'red', xlim = c(0, 1000), ylim = c(0, 20), main = '', xlab = '')
par(new = T)
hist(d$cv[51:100], col = 'blue', xlim = c(0, 1000), ylim = c(0, 20), main = '1:50 (red) vs. 51:100 (blue)', xlab = '')

f:id:TJO:20190918182518p:plain

明らかに目的変数の分布が大きく上下にスライドしていることが分かります。このようなデータを機械学習系の手法で取り扱うのは困難であろうと思われます。



これは、6年も前の話ですがこのブログで計量時系列分析について一連のシリーズ記事を書いた際に、一番最初に挙げていたポイントを思い起こせば容易に理解できると思います。ちょっと引用してみましょう。

まず、弱定常性は過程の期待値と自己共分散が時間を通じて一定である、というものです。これは想像しやすいと思います。

任意のtとkに対して、

E(y_t)=\mu
Cov(y_t,y_{t-k})=E[(y_t - \mu)(y_{t-k} - \mu)] = {\gamma}_k

が成立する場合、過程は弱定常といわれる

一方、強定常性は同時分布が不変である、というものです。

任意のtとkに対して、(y_t, y_{t+1}, \cdots , y_{t+k})'の同時分布が同一である場合、過程は強定常といわれる

基本的には、機械学習系の回帰モデルで扱うデータは最低でも弱定常、うっかりすると強定常を仮定しているのではないでしょうか。即ち「学習データもテストデータも原則として同一の分布から生成されたものと仮定する」というわけです。これはランダムフォレストのような枯れた手法でも、Deep Learning系の〇〇Netのような最新手法でも、大きく変わらないはずです。実は5年前に出版した拙著でも、以下のような図でこの概念についての説明を試みたことがあります。

f:id:TJO:20190917232920p:plain
f:id:TJO:20190917232937p:plain

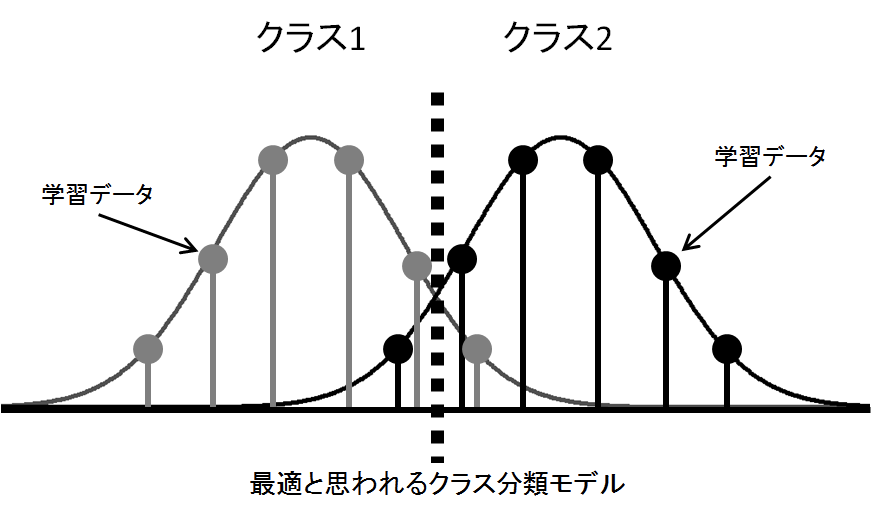
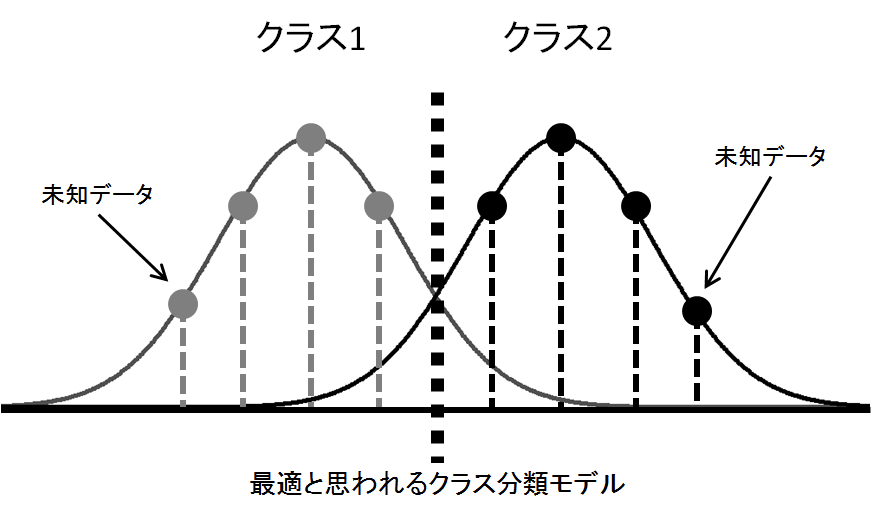
要は「機械学習は『学習データとテストデータを通じて全体として目的変数の分布が不変である（もしくは変化があっても既知である）』ことを前提としている」のですが、これに対して強い自己相関（系列相関）＝顕著なトレンドを伴う時系列データだとそもそも目的変数の分布自体が不変どころかどんどんスライドしていってしまうので、どのようにモデルを推定しても全く合わないというわけです。


そこで、上のプロットにベイジアンモデリングで推定した長期トレンドをオレンジ色で重ね書きしてみるとこうなります。

matplot(cbind(d_train$cv, pred, pred.rfday, cumsum(trend)), type = 'l', lty = 1,
        lwd = c(2, 3, 3, 5), ylab = '', xlim = c(0, 100), ylim = c(150, 1050),
        col = c(1, 2, 3, 'orange'))
segments(91, 0, 91, 1100, lty = 3, col = 1, lwd = 2)
par(new = T)
matplot(cbind(d_test$cv, validate, validate.rfday, cumsum(val_trend) + cumsum(trend)[nrow(d_train)]), type = 'l', lty = 1,
        col = c('blue', 'purple', '#008000', 'orange'),
        lwd = c(2, 3, 3, 5), ylab = '', xlim = c(-91, 9), ylim = c(150, 1050),
        axes = F)
legend('topleft', legend = c('Data', 'Fitted TS', 'Fitted RF w day',
                             'Actual', 'Forecast TS', 'Forecast RF w day',
                             'Trend'),
       lty = 1, lwd = rep(c(2, 3, 3, 5), 2),
       col = c(1, 2, 3, 'blue', 'purple', '#008000', 'orange'),
       ncol = 2, cex = 0.75)

f:id:TJO:20190918012152p:plain

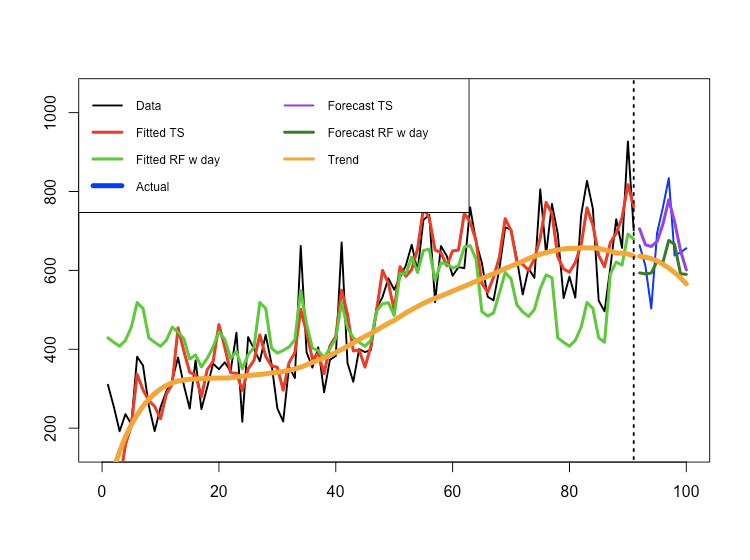
当然ですが、ランダムフォレストはこの長期トレンドを捉えることが全く出来ていません。このようなデータに対して、機械学習系の手法ではうまく扱えない理由はこれで大体説明がつくと考えられます。


ちなみに元の指摘では「ARMA*4のような定常過程モデルであっても機械学習系の手法よりも時系列予測では有利」という趣旨のことが言われているようですが、正直これは僕の浅学では良く分かりませんでした。もしかしたら、これも結局は時系列データの中で確率的に振る舞う部分をどれだけ織り込めるかという定式化の部分の差なのかなと思ったのですが、確信がないので余計なコメントは差し控えることとします。


とは言え、この辺の事情がつまるところ「株価を機械学習で予想させようとしても上手くいかない」理由でもあることは間違いないと思います。ちなみに単一の株価を単変量モデリングして予測するのは計量時系列モデルでも基本的には無理、というか出来ていたら考案した人は既に大金持ちになっているはずだと付記しておきます。。。


余談

ところで、@hayashiyusさんからは以下のようなコメントをいただきました。

古典的な計量時系列モデルと機械学習モデルとのハイブリッドにするというのは、良案だなと思った次第です。


最後に、今回の僕のR / Stan実装はかなり酷い有様なので、きちんと学びたいという方は以前の書評記事でも絶賛したこちらの一冊をぜひご参考になさってください。

実践Data Scienceシリーズ RとStanではじめる ベイズ統計モデリングによるデータ分析入門

実践Data Scienceシリーズ RとStanではじめる ベイズ統計モデリングによるデータ分析入門

というか自分がこれを読んでちゃんと現代的なStanの書き方を覚えろって話ですねorz　お粗末様でした。


追記

その1


直感的に考えればLSTMでいけるのではないかという気は実は僕もしているのですが、その割にLSTMで社会・ファイナンス時系列データの予測がうまくいったという話をなかなか聞かないので、詳しい方からのコメントがあるまでは一旦保留とします。


ただし、「トレンドを表す特徴量を加えれば良い」というのは解決策になりにくいように思います。何故なら、学習データには目的変数の増加率などの名目でトレンドを表す説明変数を与えることが出来ますが、そもそも目的変数が未知であるテストデータにはそのようなものは与えようがないからです。これが（あくまでも可能だというレベルですが）計量時系列モデルであれば出来る、という側面を今回の実験では強調しています。

その2


トレンドへの対処として、「見せかけの回帰」を回避するのと同様に目的変数の一階差分を取って差分過程に直すという考え方もあります。

とはいえ、差分過程はそもそも様々な情報が「落ちて」しまうのと、また共和分関係にある変数がある場合にはこれはこれで（VARモデルに限らず）機械学習モデルに悪さをする可能性がなきにしもあらずという気もするので、ベストな解決策かというと確信がないです。。。

その3


cv_i = q_i + season_i + trend_i
q_i = \displaystyle \sum^{3}_{j = 1} \beta_j x_j, ~ q_i \sim Normal (\mu_q, s_q)
r_i = \displaystyle \sum^{7}_{j = 1} season_j + \epsilon_{r}, ~ \epsilon_r \sim Normal(0, s_r)
trend_i - trend_{i - 1} = trend_{i - 1} - trend_{i - 2} + \epsilon_{trend}, ~ \epsilon_{trend} \sim Normal(0, s_{trend})

モデルを見ての通り、これは統計モデリングという意味では変量・混合効果モデルになっているわけです（故に階層ベイズでパラメータ推定する流れになっている）。なので、変量効果を織り込む方法論があれば機械学習系の手法でもやれるような気がしてきました。

*1:ここではpredictとは異なり「未来方向の未知の値を予測する」という含意

*2:ちなみに季節調整の効果に十分な大きさがなければ推定結果はゼロに落ちる

*3:何故ならトレンドを表す特徴量が与えられておらず、仮に学習データ側で定義してもテストデータではそもそも定義しようがないため

*4:ARIMAと違ってI（和分）過程が抜けていて定常過程