追記(2016年8月22日)
{rBayesianOptimization}の使い方を間違えていて、この記事の下部では実際にはテスト誤差ではなくトレーニング誤差を評価してしまっていますorz 実際にはScore返値にholdoutを入れるのが正解です。別に{rBayesianOptimization}単体で取り上げた記事を書きましたので、正しい使い方はそちらをお読みください。
Deep Learningをだらだらと実践してみるこのシリーズ、前回は分類だったので今回は回帰でやってみようと思います。お題はUCI ML repositoryの"Online News Popularity"です。とあるサイトに掲載されたオンラインニュース記事がそれぞれどれくらいシェア(おそらくSNS類に)されたかを、様々な特徴量と合わせて収めた39644行×61列のデータセットです。
元のニュース記事が非公開である代わりに、特徴量の中には例えばLDAにかけた時の各トピックに属する確率とかsentiment analysisの結果とかも含まれていて、ある意味極めて綺麗に前処理済みのデータと見ることも出来るかと思います。いわば至れり尽くせりのデータセットですね(笑)。これをDeep Learningで回帰してやろうというのが今回の目標です。
なおいつもながらのお断りですが、この記事はあくまでも僕個人の備忘録的なMXnetの実行例メモ的な何かです。本当にちゃんとDeep Learningを実践したい方や他のTensorFlow / Chainer / Kerasなどなどでの実践例をご覧になりたい方はこんな駄文ではなく他の記事を是非ご参照くださいorz
下準備
今回は普通に上記の本家サイトからそのままローカルにDLしてきて、以下のように普通にインポートして下さい。
> d <- read.csv('OnlineNewsPopularity.csv') > d <- d[,-c(1,2)] > idx <- sample(nrow(d),5000,replace=F) > d_train <- d[-idx,] > d_test <- d[idx,]
全部で61列ありますが、最初の2列はnon-predictiveなので削除します。その上で適当に5000行だけ分けてholdoutのテストデータとして、残りを学習データとします。なお、ここで目的変数となるsharesをヒストグラムにしてみるとこうなります。
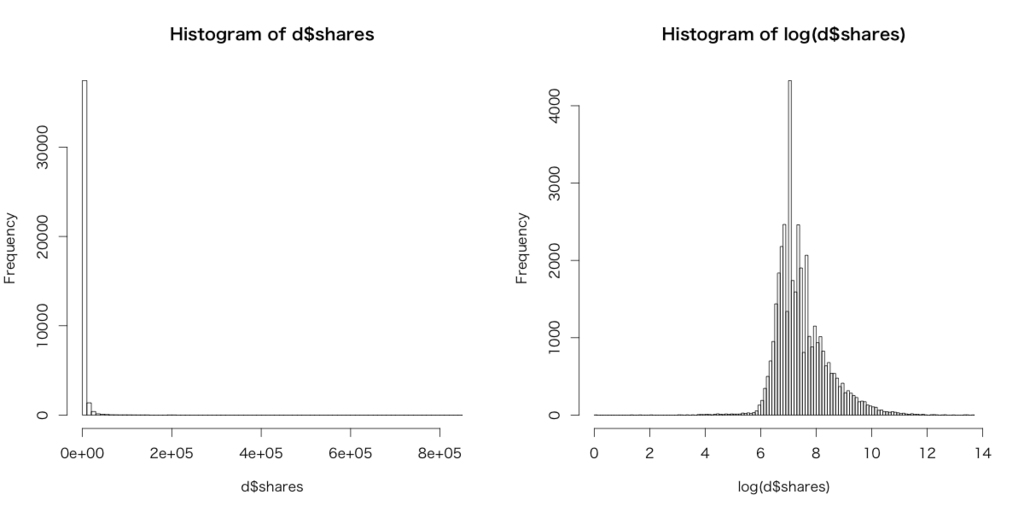
ということで、以後目的変数であるsharesは対数変換した方が良さそうだと思われます。
ベンチマーク(L1正則化回帰&ランダムフォレスト)
先にL1正則化線形回帰してみます。テストデータに対する当てはまり具合はRMSEで評価してみました。ただし手計算が面倒だったので{Metrics}パッケージのrmse関数を使ってます。L1正則化線形回帰は{glmnet}パッケージを用いて回しました。
> library(glmnet) > d_train.glmnet <- cv.glmnet(as.matrix(d_train[,-59]),log(d_train[,59]),family='gaussian',alpha=1) > plot(d_train.glmnet) > plot(log(d_test$shares), predict(d_train.glmnet, newx=as.matrix(d_test[,-59]), s=d_train.glmnet$lambda.min)) > library(Metrics) > rmse(log(d_test$shares), predict(d_train.glmnet, newx=as.matrix(d_test[,-59]), s=d_train.glmnet$lambda.min)) [1] 0.8697543
それなりの数字になったように思われます。次にランダムフォレスト回帰してみます。4万行とそれなりに行数も多い上に58列と特徴次元も小さくないので、tuneRFは省略してチューニングなしで回してあります。
> d_train.rf <- randomForest(log(shares)~.,d_train) > rmse(log(d_test$shares), predict(d_train.rf,newdata=d_test[,-59])) [1] 0.8504932
MXnetでDNNを組んで回してみる
まずはMXnetを使って、基本通りのDNNを組んでみます。最初にデータセットをMXnetのフォーマットに合わせます。また前回懲りたので、事前に特徴量は全て正規化しておきます*1。
# フォーマッティング > library(mxnet) > train <- data.matrix(d_train) > test <- data.matrix(d_test) > train.x <- train[,-59] > train.y <- train[,59] > test.x <- test[,-59] > test.y <- test[,59] # 正規化 > train_means <- apply(train.x, 2, mean) > train_stds <- apply(train.x, 2, sd) > test_means <- apply(test.x, 2, mean) > test_stds <- apply(test.x, 2, sd) > train.x <- t((t(train.x)-train_means)/train_stds) > test.x <- t((t(test.x)-test_means)/test_stds) # 目的変数を対数変換 > train.y <- log(train.y) > test.y <- log(test.y)
では、普通に回してみましょう。とりあえず中間層3層で、ユニット数は特徴次元数の4倍-4倍-2倍ぐらいで適当に決め打ちして回してみます。ちなみに今回は線形回帰を出力するため、出力はmx.symbol.LinearRegressionOutput関数とし、直前の全結合層のユニット数は1にする必要があります。
> data <- mx.symbol.Variable("data") > fc1 <- mx.symbol.FullyConnected(data, name="fc1", num_hidden=220) > act1 <- mx.symbol.Activation(fc1, name="tanh1", act_type="tanh") > drop1 <- mx.symbol.Dropout(act1, p=0.5) > fc2 <- mx.symbol.FullyConnected(drop1, name="fc2", num_hidden=220) > act2 <- mx.symbol.Activation(fc2, name="tanh2", act_type="tanh") > drop2 <- mx.symbol.Dropout(act2, p=0.5) > fc3 <- mx.symbol.FullyConnected(drop2, name="fc3", num_hidden=110) > act3 <- mx.symbol.Activation(fc3, name="tanh3", act_type="tanh") > drop3 <- mx.symbol.Dropout(act3, p=0.5) > fc4 <- mx.symbol.FullyConnected(drop3, name="fc4", num_hidden=1) > output <- mx.symbol.LinearRegressionOutput(fc4, name="linreg") > devices <- mx.cpu() > mx.set.seed(71)
またモデル計算部分でも、eval.metricをRMSEにする必要があるのでmx.metric.rmseメソッドを引数として渡さなければいけません。残りは前回とほぼ同様です。
> model <- mx.model.FeedForward.create(output, X=train.x, y=train.y, ctx=devices, num.round=100, array.batch.size=100, learning.rate=1e-5, momentum=0.99, eval.metric=mx.metric.rmse, initializer=mx.init.uniform(0.5), array.layout = "rowmajor", epoch.end.callback=mx.callback.log.train.metric(100))
後は普通にpredictメソッドで結果が出せます(回帰なので単なる予測値がnumericで出てくるだけで、softmaxでの分類の時のようにクラス分類確率が並んでいるわけでもなく特に転置したりする必要はない)。RMSEを算出してみたらこうなりました。
> preds <- predict(model, test.x, array.layout='rowmajor') > rmse(preds, test.y) [1] 0.8990231
L1正則化線形回帰に負けてますorz さて、どうやって挽回しましょうか?
MXnetで手動で試行錯誤する
考え方としては幾つかあって、前回色々試してみた印象では「中間層第1層のユニット数を極端に大きくし、以後の中間層では急激に絞っていく」戦略が良さそうだという感じでした。そこで特徴次元数の6倍-1/2倍-1/6倍というようにしてみます。またMXnetのdocを見ているとDropoutをp=0.2ぐらいで突っ込むと良いらしい*2ので、教科書通りのp=0.5よりも低く設定して各層に追加してみます。
> data <- mx.symbol.Variable("data") > fc1 <- mx.symbol.FullyConnected(data, name="fc1", num_hidden=360) > act1 <- mx.symbol.Activation(fc1, name="tanh1", act_type="tanh") > drop1 <- mx.symbol.Dropout(act1, p=0.2) > fc2 <- mx.symbol.FullyConnected(drop1, name="fc2", num_hidden=30) > act2 <- mx.symbol.Activation(fc2, name="tanh2", act_type="tanh") > drop2 <- mx.symbol.Dropout(act2, p=0.2) > fc3 <- mx.symbol.FullyConnected(drop2, name="fc3", num_hidden=10) > act3 <- mx.symbol.Activation(fc3, name="tanh3", act_type="tanh") > drop3 <- mx.symbol.Dropout(act3, p=0.2) > fc4 <- mx.symbol.FullyConnected(drop3, name="fc4", num_hidden=1) > output <- mx.symbol.LinearRegressionOutput(fc4, name="linreg") > devices <- mx.cpu() > mx.set.seed(71) > model <- mx.model.FeedForward.create(output, X=train.x, y=train.y, ctx=devices, num.round=250, array.batch.size=200, learning.rate=2e-4, momentum=0.99, eval.metric=mx.metric.rmse, initializer=mx.init.uniform(0.5), array.layout = "rowmajor", epoch.end.callback=mx.callback.log.train.metric(20)) Start training with 1 devices [1] Train-rmse=4.04064720979636 [2] Train-rmse=1.38074657462996 [3] Train-rmse=1.10266792563435 # ... # [249] Train-rmse=0.869960972252981 [250] Train-rmse=0.868855651931648 > preds <- predict(model, test.x, array.layout='rowmajor') > rmse(preds, test.y) [1] 0.8695997
ゼイゼイ、ようやくL1正則化線形回帰に勝ちました*3。というように、Deep Learning全般は特に中間層が多い場合にはものすごくパラメータチューニングが面倒です。
ベイズ最適化でチューニングを効率良く進める
これをずっと手動でやり続けるのは非効率なので、{rBayesianOptimization}パッケージを使ってベイズ最適化でパラメータチューニングしてみようと思います。この文脈におけるベイズ最適化とは、端的に言えば「Deep Learningのモデルの精度がより向上するようにパラメータ空間をベイズ的に探索することで高速で最適なパラメータを探し出す」ということ、のようです。
なお、Deep Learningのパラメータチューニングのベイズ最適化の話題については例えば[twitter:@issei_sato]先生の医用画像読影支援に関するslideshareや、id:olanleedさんの以下の記事、我らがid:hoxo_m親分の以下の記事などが分かりやすいかと思います。
ちなみに以下のコードは全部オールインワンで回せるように、データを入れるところから全部まとめて改めてスクリプトにしてあります。コマンドプロンプト部をエディタなどで一括削除してからお使い下さい。
> d <- read.csv('OnlineNewsPopularity.csv') > d <- d[,-c(1,2)] > idx <- sample(nrow(d),5000,replace=F) > d_train <- d[-idx,] > d_test <- d[idx,] > library(mxnet) > train <- data.matrix(d_train) > test <- data.matrix(d_test) > train.x <- train[,-59] > train.y <- train[,59] > test.x <- test[,-59] > test.y <- test[,59] > train_means <- apply(train.x, 2, mean) > train_stds <- apply(train.x, 2, sd) > test_means <- apply(test.x, 2, mean) > test_stds <- apply(test.x, 2, sd) > train.x <- t((t(train.x)-train_means)/train_stds) > test.x <- t((t(test.x)-test_means)/test_stds) > train.y <- log(train.y) > test.y <- log(test.y) > mxnet_holdout_bayes <- function(unit1, unit2, unit3, num_r, learn_r){ + data <- mx.symbol.Variable("data") + fc1 <- mx.symbol.FullyConnected(data, name="fc1", num_hidden=unit1) + act1 <- mx.symbol.Activation(fc1, name="tanh1", act_type="tanh") + drop1 <- mx.symbol.Dropout(act1, p=0.2) + fc2 <- mx.symbol.FullyConnected(drop1, name="fc2", num_hidden=unit2) + act2 <- mx.symbol.Activation(fc2, name="tanh2", act_type="tanh") + drop2 <- mx.symbol.Dropout(act2, p=0.2) + fc3 <- mx.symbol.FullyConnected(drop2, name="fc3", num_hidden=unit3) + act3 <- mx.symbol.Activation(fc3, name="tanh3", act_type="tanh") + drop3 <- mx.symbol.Dropout(act3, p=0.2) + fc4 <- mx.symbol.FullyConnected(drop3, name="fc4", num_hidden=1) + output <- mx.symbol.LinearRegressionOutput(fc4, name="linreg") + devices <- mx.cpu() + mx.set.seed(71) + model <- mx.model.FeedForward.create(output, X=train.x, y=train.y, ctx=devices, num.round=num_r, array.batch.size=200, learning.rate=learn_r, momentum=0.99, eval.metric=mx.metric.rmse, initializer=mx.init.uniform(0.5), array.layout = "rowmajor", epoch.end.callback=mx.callback.log.train.metric(20), verbose=FALSE) + ptrain <- predict(model, train.x, array.layout='rowmajor') + preds <- predict(model, test.x, array.layout='rowmajor') + train_score <- rmse(ptrain, train.y) + holdout_score <- rmse(preds, test.y) + list(Score=-train_score, Pred=-holdout_score) # 「最大化」されてしまうので、最小化したい場合はメトリクスを負にする + } > library(Metrics) > library(rBayesianOptimization) > opt_res <- BayesianOptimization(mxnet_holdout_bayes, + bounds=list(unit1=c(60L,120L), + unit2=c(30L,60L), + unit3=c(10L,30L), + num_r=c(15L,50L), + learn_r=c(1e-5,1e-3)), + init_points=10, n_iter=1, acq='ucb', kappa=2.576, eps=0.0, verbose=TRUE) elapsed = 11.21 Round = 1 unit1 = 119.0000 unit2 = 40.0000 unit3 = 24.0000 num_r = 26.0000 learn_r = 0.0007 Value = -0.8769 # ... # elapsed = 17.70 Round = 11 unit1 = 60.0000 unit2 = 60.0000 unit3 = 10.0000 num_r = 50.0000 learn_r = 0.0005 Value = -0.8705 Best Parameters Found: Round = 7 unit1 = 95.0000 unit2 = 55.0000 unit3 = 24.0000 num_r = 49.0000 learn_r = 0.0008 Value = -0.8672
意外とあっさり0.8672まで来ました。もうちょっと色気出してみましょう。。。と言いながら何度も何度もベイズ最適化で試行錯誤とかいう不毛なこと*4を繰り返すこと幾度、0.8609、0.8565、0.8511と徐々に改善していって、最終的に以下のような結果が得られました。
> opt_res <- BayesianOptimization(mxnet_holdout_bayes, + bounds=list(unit1=c(300L,500L), + unit2=c(30L,70L), + unit3=c(10L,40L), + num_r=c(50L,150L), + learn_r=c(1e-5,1e-3)), + init_points=10, n_iter=1, acq='ucb', kappa=2.576, eps=0.0, verbose=TRUE) elapsed = 51.54 Round = 1 unit1 = 316.0000 unit2 = 38.0000 unit3 = 10.0000 num_r = 93.0000 learn_r = 0.0006 Value = -0.8629 # ... # elapsed = 84.89 Round = 11 unit1 = 335.0000 unit2 = 31.0000 unit3 = 40.0000 num_r = 150.0000 learn_r = 0.0010 Value = -0.8490 Best Parameters Found: Round = 11 unit1 = 335.0000 unit2 = 31.0000 unit3 = 40.0000 num_r = 150.0000 learn_r = 0.0010 Value = -0.8490
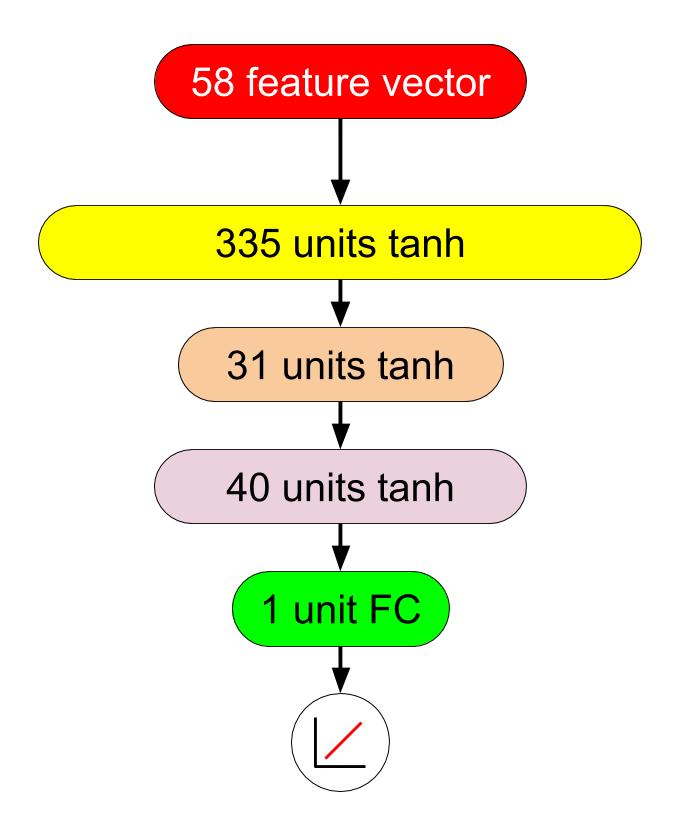
0.8490、これでついにランダムフォレストを上回りました。この段階でのベストのDNNは335-31-40の中間層3層、学習係数減衰率は1e-3、epoch数は150(ミニバッチは100)ということになりました。
最後に
もう見ての通りで、ろくろく何もチューニングしなかったランダムフォレストの0.8505を超えるのにDeep LearningというかDNNではここまでの努力が必要になったというのが物凄くつらいですね(汗)。ベイズ最適化様々でございます。
そして{rBayesianOptimization}パッケージについては、後日別に改めて記事にまとめようかなと思います。当たり前ながら、Deep Learningのためだけに特化したパッケージではないので、他にも色々応用できそうだなと。ただし「ベイズ最適化はランダムサーチより実は効率が悪い」という指摘もあるようなので、あくまでもパラメータチューニング自動化の一つの方策としての紹介になるかもです。
ランダムサーチの方が簡単にできるじゃん、という気もしますがそこはまた置いといてということで。。。特にDeep Learningだとパラメータ数自体が多くて、単にランダムサーチするだけでも物凄い計算負荷になると思うので。