今年のKDD cupが絵に描いたような不均衡データ(正例と負例との数的比率が極端に偏っているデータ)で苦労させられたので、ちょっと調べたら色々と良い方法があるなぁと気が付きましたよということで備忘録的に紹介しておきます。
ちなみにググったら普通に@sfchaosさんのslideshareが出てきたので、僕なんぞの解説よりそちらをどうぞw
なおこちらのスライドの方がSVM以外にもランダムフォレストなどでの対処法も載っているので、汎用的だと思います。。。
クラス重み付けを調整してサンプルサイズが小さい方のクラスの影響力を上げてやる
これはRのsvm{e1071}の説明だと割とあっさりとしか書かれてないので、どちらかというとPythonのsklearn.svm.SVCの説明を見た方が分かりやすいかもしれません。
要は、不均衡データだとサンプルが多い方のクラス(正例の方が多ければ正方向に、負例の方が多ければ負方向に)に引っ張られてしまうわけです。
実際、今年のKDD cupでは学習データの正例と負例の比率が数百倍ぐらい異なっていた(学習データは負例の方が圧倒的に多かったのにテストデータは正負で半々)ので、普通にSVMなりランダムフォレストなりで分類器を作ってテストデータを分類してみると、「全部負」みたいなテスト分類結果ばっかり。。。これではどうにもならないという。
そこで、例えばSVMであればマージン*1のところに正例と負例とで異なる重み付けをかけることでペナルティの量を変える→クラス分類結果にも意図的にバイアスをかけて正例の検出感度を上げる、みたいなことをしてやるというのがここで提案されている解決策です。
やり方は単純で、Rのsvm{e1071}ならclass.weights引数に、Pythonのsklearn.svm.SVCならclass_weight引数に、それぞれ正例と負例にかける重み付けの値を指定して入れてやるだけです。
値の目安ですが、基本的には2つのクラスのサンプルサイズ比を取り、多い方のクラスを1に固定して少ない方のクラスにはその比率をかける、というのが一般的なようです。それだけ少ない方のクラスに強めの影響力を持たせてやる、という感じですかね。
実際にRのsvm{e1071}でやってみる
久しぶりにGitHubに新しいサンプルデータを上げておいたので、落としてきてxorcという名前でインポートしておきましょう。一応、以下のように直しておきます。ついでに決定境界も描きたいのでグリッドを切っておきます。
> xorc <- read.delim("~/Dev/R/Blog/xorc_ub.txt") > xorc$label<-as.factor(xorc$label) > head(xorc) x y label 1 0.41864961 2.15143734 0 2 -0.08999971 1.81652176 0 3 -0.36083303 2.39957415 0 4 1.46543814 -0.73478552 0 5 0.70992029 0.49014989 0 6 1.04577669 0.08886517 0 > summary(xorc$label) 0 1 600 20 > plot(xorc[,-3],pch=19,col=c(rep('blue',600),rep('red',20)),cex=2,xlim=c(-4,4),ylim=c(-4,4))
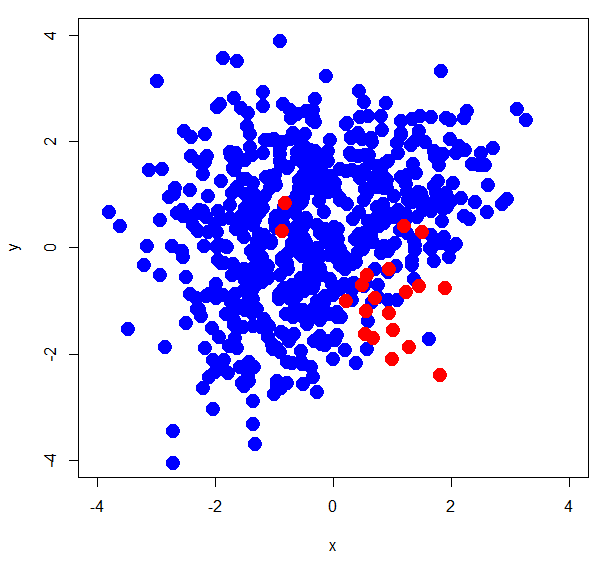
正例が20個、負例が600個というかなり偏りのあるデータであることが分かります。では、実際にsvm{e1071}で分類してみましょう。
> library(e1071) > xorc.svm<-svm(label~.,xorc) > xorc.prd<-predict(xorc.svm,newdata=xorc[,-3]) > table(xorc$label,xorc.prd) xorc.prd 0 1 0 600 0 1 19 1 # デフォルトの再予測結果 > xorc_wts.svm<-svm(label~.,xorc,class.weights = c('0'=1,'1'=30)) # クラス重み付けはclass.weights = c('ラベルのカテゴリ1' = 重みの値1, 'ラベルのカテゴリ2' = 重みの値2,...) # という書式で与えてやる。3クラス以上でも使える > xorc_wts.prd<-predict(xorc_wts.svm,newdata=xorc[,-3]) > table(xorc$label,xorc_wts.prd) xorc_wts.prd 0 1 0 546 54 1 2 18 # クラス重み付けをかけた時の再予測結果
1つ目の計算はデフォルトパラメータでやったものですが、学習データに対して再予測をかけているにもかかわらず正例が1個しかないというクラス分類結果になってしまっています。一方、2つ目の計算は正例に30倍の倍率となるようなクラス重み付けをかけたところ、再予測では正例が18個というクラス分類結果になっています。
そこで、決定境界を描いて実際にどうなっているかを見てみましょう。
> px<-seq(-4,4,0.03) > py<-seq(-4,4,0.03) > pgrid<-expand.grid(px,py) > names(pgrid)<-c("x","y") # 決定境界を描くためにグリッドを切る > out.xorc.svm<-predict(xorc.svm,pgrid,type="vector") > out.xorc_wts.svm<-predict(xorc_wts.svm,pgrid,type="vector") # グリッド上に決定境界のもととなるラベルを算出する > par(mfrow=c(1,2)) > plot(xorc[,-3],pch=19,col=c(rep('blue',600),rep('red',20)),cex=2,xlim=c(-4,4),ylim=c(-4,4),main='Without class weights') > par(new=T) > contour(px,py,array(out.xorc.svm,dim=c(length(px),length(py))),xlim=c(-4,4),ylim=c(-4,4),col="purple",lwd=3,drawlabels=F) > plot(xorc[,-3],pch=19,col=c(rep('blue',600),rep('red',20)),cex=2,xlim=c(-4,4),ylim=c(-4,4),main='With class weights') > par(new=T) > contour(px,py,array(out.xorc_wts.svm,dim=c(length(px),length(py))),xlim=c(-4,4),ylim=c(-4,4),col="purple",lwd=3,drawlabels=F) # 決定境界を描画する
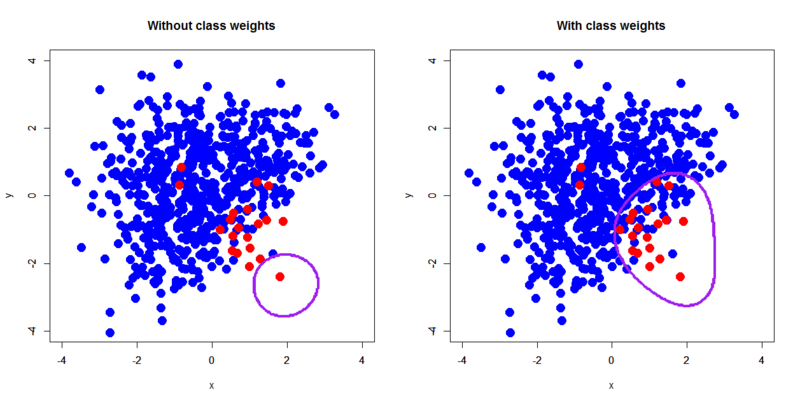
これで一目瞭然でしょう。デフォルトだと負例が作り出す大きな決定境界によって正例が覆い尽くされてしまうのに対して、クラス重み付けを調整することで正例が負例を押し返すような形で決定境界が均衡する感じになるわけですね。ちなみにsvm{e1071}のヘルプでは最も簡単なクラス重み付けの与え方として
> wts<-100/table(xorc$label) > wts 0 1 0.1666667 5.0000000
という書き方を挙げていて、この方が正例負例のカウントをしなくて良い上にclass.weights引数に与える際にこのまま渡してやれば良いので手っ取り早いと思いますw
一つ注意したいのが、クラス重み付けをかけると正例のクラス分類は増えるんですが、負例の誤分類も増えてしまうこと。今回のサンプルデータではあえて負例が正例と大幅に重なるように作ってあるので、クラス重み付けによってfalse alarmが多くなる結果になっています。この辺は実際の分類問題において何を重視するかにもよると思うので、検討を要するポイントだと思います。
*1:初版ではヒンジ損失と誤って書いておりましたごめんなさい