これは単なる備忘録です。詳細を知りたいという方は、この記事の元ネタになった以下のid:sinhrksさんの記事をお読みください。
ここでの問題意識は非常にシンプルで「そもそも時系列クラスタリングをかなり膨大な行数のデータに対して実行する際にどれほど厳密にやるべきか?」というお話です。というのも、たかだか数百行ぐらいのデータならリンク先にもあるように動的時間伸縮法(Dynamic Time Warping: DTW)で距離行列を求めてhclust関数で動く階層的クラスタリングでやるのが正しいと思うのですが、これが1万行とか10万行とかになるとそもそもdiss関数やhclust関数が重過ぎて動かないわけです。
そういうケースで、例えば原理的には正しくないのを承知の上で単純なK-means(リンク先にあるような{flexclust} + DTWでやるのではなく)でやっても、それなりの精度が出せるのであれば「仮に」使う目的で代用しても良いのかどうか?というのが気になった、というのが今回の記事のモチベーションです。言い方は悪いですが「K-meansで何とかなるのなら大規模データにはK-meansで代用してしまう」が是か非かを知りたい、ということです。
ということで、面倒なので一気に本題に行きたいと思います。
上昇トレンド・平均回帰・下降トレンド・季節調整あり時系列を用意する
やることは以下のRスクリプトを回すだけです。完全にリンク先の記事を踏襲していますが、季節調整っぽいものを加えるために適当にsinカーブを異なる周期で加えたものを2つ追加しています。
> # 各グループの系列数 > N <- 20 > # 系列の長さ > SPAN <- 24 > # トレンドが上昇/ 下降する時の平均値 > TREND <- 0.5 > > generate_ts <- function(m, label) { + library(dplyr) + # ランダムな AR 成分を追加 + .add.ar <- function(x) { + x + arima.sim(n = SPAN, list(ar = runif(2, -0.5, 0.5))) + } + # 平均が偏った 乱数を cumsum してトレンドとする + d <- matrix(rnorm(SPAN * N, mean = m, sd = 1), ncol = N) %>% + data.frame() %>% + cumsum() + d <- apply(d, 2, .add.ar) %>% + data.frame() + colnames(d) <- paste0(label, seq(1, N)) + d + } > > set.seed(101) > group1 <- generate_ts(TREND, label = 'U') > set.seed(102) > group2 <- generate_ts(0, label = 'N') > set.seed(103) > group3 <- generate_ts(-TREND, label = 'D') > set.seed(104) > group4 <- generate_ts(0, label = 'S1_') > group4 <- group4 + 5*sin(seq(0, 4*pi, length.out = SPAN)) > set.seed(105) > group5 <- generate_ts(0, label = 'S2_') > group5 <- group5 + 5*sin(seq(0, 8*pi, length.out = SPAN)) > > data <- cbind(group1, group2, group3, group4, group5) > data <- as.data.frame(data) > matplot(data, type = 'l', lty = 1, col = c(rep(1,20), rep(2,20), rep(3,20), rep(4,20), rep(5,20))) > true.cluster <- c(rep(1,20), rep(2,20), rep(3,20), rep(4,20), rep(5,20))

こんな感じの時系列になると思います。
単純なK-meansでやってみる
横持ちのデータを縦持ちに直せば、普通にkmeans関数で回せます。
> model.km <- kmeans(t(data), centers = 5) > model.km$cluster U1 U2 U3 U4 U5 U6 U7 U8 U9 U10 U11 U12 U13 1 3 1 3 3 4 1 3 3 3 4 1 1 U14 U15 U16 U17 U18 U19 U20 N1 N2 N3 N4 N5 N6 1 3 1 1 1 3 4 1 1 4 5 5 5 N7 N8 N9 N10 N11 N12 N13 N14 N15 N16 N17 N18 N19 1 1 5 2 5 5 4 5 5 4 1 4 5 N20 D1 D2 D3 D4 D5 D6 D7 D8 D9 D10 D11 D12 4 2 2 2 5 2 2 2 2 2 2 5 5 D13 D14 D15 D16 D17 D18 D19 D20 S1_1 S1_2 S1_3 S1_4 S1_5 2 2 2 2 5 2 5 5 4 5 4 4 1 S1_6 S1_7 S1_8 S1_9 S1_10 S1_11 S1_12 S1_13 S1_14 S1_15 S1_16 S1_17 S1_18 5 5 5 5 4 5 5 5 1 5 5 5 5 S1_19 S1_20 S2_1 S2_2 S2_3 S2_4 S2_5 S2_6 S2_7 S2_8 S2_9 S2_10 S2_11 4 2 5 4 4 4 4 1 4 4 2 4 4 S2_12 S2_13 S2_14 S2_15 S2_16 S2_17 S2_18 S2_19 S2_20 4 2 4 4 5 5 5 5 4 > table(true.cluster, model.km$cluster) true.cluster 1 2 3 4 5 1 9 0 8 3 0 2 5 1 0 5 9 3 0 14 0 0 6 4 2 1 0 5 12 5 1 2 0 12 5 > matplot(data, type = 'l', lty = 1, col = model.km$cluster)
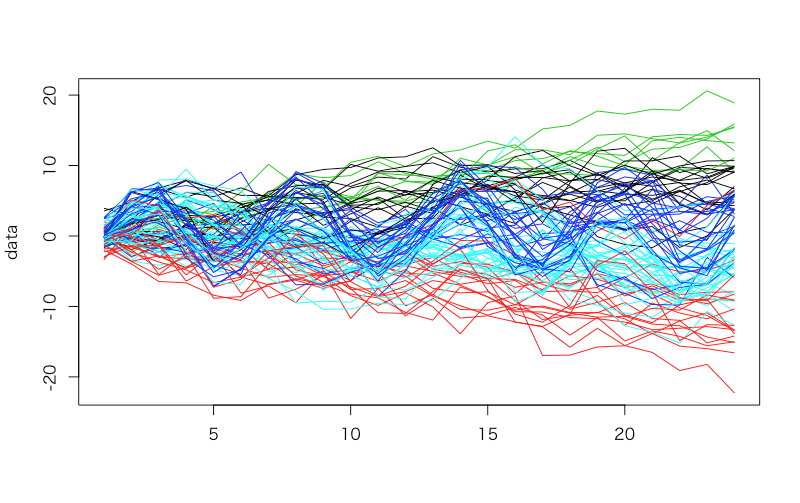
パッと見ではそれほど悪くないように見えるんですが、confusion matrix的なものを出して「それぞれの行の最大値」を正解の場合の数とみなして計算すると、正答率は56%に留まります
{TSclust}のDTWで階層的クラスタリングをやってみる
これは完全にリンク先を踏襲しています。
> # DTW 距離で距離行列を作成 > d <- diss(data, "DTWARP") > # hclust は既定で実行 = 最遠隣法 > h <- hclust(d) > par(cex=0.6) > plot(h, hang = -1) > h.cluster <- cutree(h, 5) > h.cluster U1 U2 U3 U4 U5 U6 U7 U8 U9 U10 U11 U12 U13 1 1 1 1 1 2 3 1 1 1 2 3 1 U14 U15 U16 U17 U18 U19 U20 N1 N2 N3 N4 N5 N6 1 1 1 3 1 1 2 3 1 2 4 4 4 N7 N8 N9 N10 N11 N12 N13 N14 N15 N16 N17 N18 N19 3 3 2 4 4 4 2 4 4 2 3 2 4 N20 D1 D2 D3 D4 D5 D6 D7 D8 D9 D10 D11 D12 2 5 4 4 4 4 4 4 5 5 5 4 2 D13 D14 D15 D16 D17 D18 D19 D20 S1_1 S1_2 S1_3 S1_4 S1_5 5 5 4 5 4 5 4 4 2 4 2 2 3 S1_6 S1_7 S1_8 S1_9 S1_10 S1_11 S1_12 S1_13 S1_14 S1_15 S1_16 S1_17 S1_18 4 4 4 4 2 4 4 4 3 4 4 2 4 S1_19 S1_20 S2_1 S2_2 S2_3 S2_4 S2_5 S2_6 S2_7 S2_8 S2_9 S2_10 S2_11 2 4 4 2 2 4 2 3 2 4 4 3 4 S2_12 S2_13 S2_14 S2_15 S2_16 S2_17 S2_18 S2_19 S2_20 4 4 2 2 4 4 4 4 2 > table(true.cluster, h.cluster) h.cluster true.cluster 1 2 3 4 5 1 14 3 3 0 0 2 1 6 4 9 0 3 0 1 0 11 8 4 0 6 2 12 0 5 0 7 2 11 0 > matplot(data, type = 'l', lty = 1, col = h.cluster) > cluster.evaluation(rep(c(1, 2, 3, 4, 5), rep(N, 5)), h.cluster) [1] 0.4774603

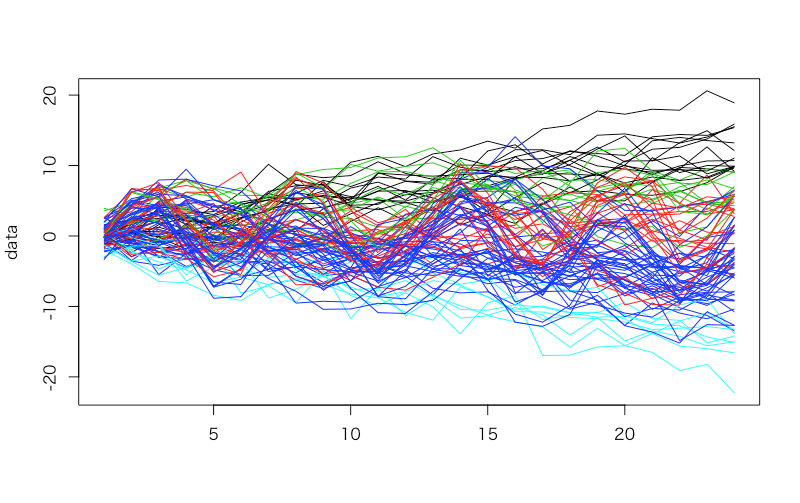
これも見た目にはそれほど悪くないような気がしますが、{TSclust}のcluster.evaluationを使うと正答率は47.7%。先ほどの理屈でconfusion matrixから計算しても57%という結果になりました。
現時点での感想
ただのK-meansを使っても{TSclust} + DTWでやってもそれほど変わらないかもしれない、という感想を持ちました。とは言え、この感想が妥当だとは正直思えない(理論的には当然このやり方は正しくない)ので、もう少し色々調べてみようと思います。。。