今月はモデルナワクチンの2回目接種*1やら仕事でも負荷の高い分析業務やら、はたまた執筆*2やらでネタ切れなのもあってあまりブログ記事を書けていなかったので、最近話題になった件について簡単に論じてみようかと思います。元ネタはこちらです。
これはイスラエルで公表されたCOVID-19ワクチンの重症化防止効果に関する統計について、いわゆる「シンプソンのパラドックス」が見られるのでそれを補正する必要があると指摘するブログ記事です。この件について僕が引用しながらボソッと放言したところ、思いの外大きな反響があったのでした。
イスラエルで起きている、「ワクチンが効いていないように見える」シンプソンのパラドックス。年齢で調整するとこうなるという分かりやすい解説https://t.co/gQrATCNzS7 pic.twitter.com/JI8Gq8h0Lk
— TJO (@TJO_datasci) 2021年8月19日
シンプソンのパラドックスというと数ある統計学のパラドックスの中でもかなりメジャーな部類に入ると思うのですが、意外にもこれがズバリ適用されるべきデータってなかなか実務では出くわさないんですよね*3。上で引用したブログ記事的には良き敵にこそござんなれという按配だったのでしょうが、反響を見ている限りでは思った以上に複雑な概念だと一般には感じられているらしいという印象がありました。
ということで、僕個人にとってもちょうど良い機会なのでシンプソンのパラドックスについて調べてみた結果を、記事としてまとめてみようと思います。なおいつもながらですが、記事内容に誤りや理解不足などあればご指摘くださると有難いです。
シンプソンのパラドックスとは
Wikipedia日英両言語版とも記事がありますが、比較の問題で言うと英語版の方が解説が親切です。英語版の記事にある以下のGIFアニメが、一番分かりやすいのではないかと思います。

(By Pace~svwiki - Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=62007681)
これを見れば一目瞭然で、要は「サンプル全体における相関とサンプルを部分的に切り出した時の部分ごとの相関とが食い違う(逆になることすらある)」という現象です。一般にはEdward H. Simpsonが1951年に発表した論文で指摘したのが初出とされますが*4、この現象自体はかなり以前から統計学界では知られていたようです。
ただし重要なポイントがWikipedia英語版の記事の冒頭に書かれていて、"The paradox can be resolved when confounding variables and causal relations are appropriately addressed in the statistical modeling"(このパラドックスは交絡因子と因果関係が統計モデリングによって適切に対処されれば解決可能である)とあります。即ち、これは統計的因果推論の文脈で交絡因子をきちんとバイアスを調整する必要のある問題だということなんですね*5。この視点を正しく持てれば適切な解釈にたどり着けるし、さもなくば容易に誤った解釈に陥ってしまう。そういう厄介なパラドックスなのだと言えそうです。
Pearl本の例で考えてみる
そんなシンプソンのパラドックスですが、ちょっと前に買ったJudea Pearlの『入門統計的因果推論』の冒頭、1.2節に分かりやすい説明が出てきます。折角なので、そこから幾つか要点を抜粋して読み解いてみましょう。
本書では、例として「10代〜50代の各年齢層における週ごとの運動量とコレステロール値」とをX軸とY軸にプロットしたものを図1.1として挙げています*6。
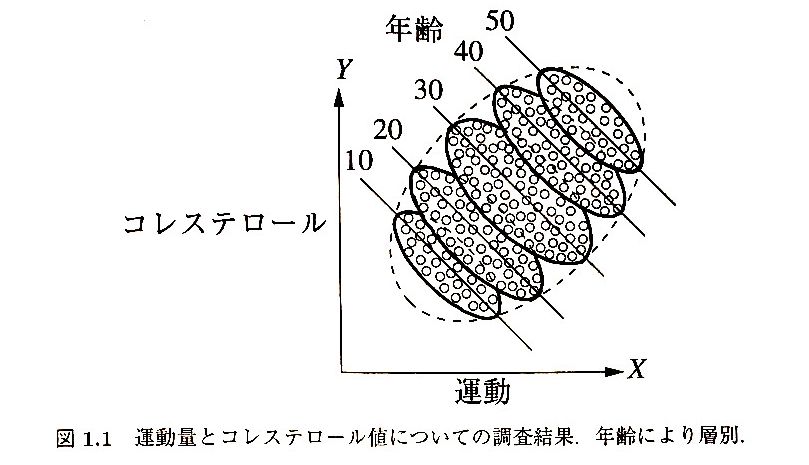
直感的にも医学的にも「よく運動している人の方がコレステロール値は低い」というのは常識で、実際に10代〜50代の各年齢層ごとに見てみると右肩下がりの傾向になっています。ところが、全ての年齢層でデータをマージしてみると、図1.2のようになってしまいます。
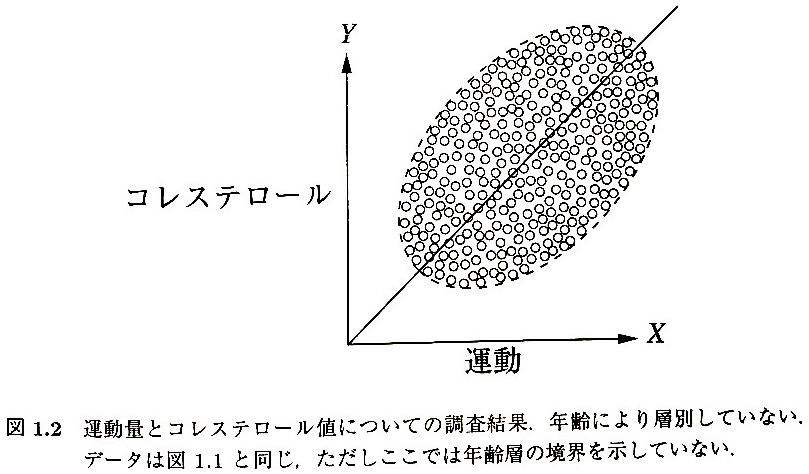
そう、何と「よく運動している人の方がコレステロール値が高い」という右肩上がりの傾向になっているのです。これは一体どういうことなのでしょうか?この点についてPearlは「この問題を解決するためには、やはりデータに隠された事実*7を使う必要がある」と述べています。即ち、
- ヒトは歳を取れば取るほど健康のために運動をするようになる
- ヒトは歳を取ると運動するかしないかにかかわらずコレステロール値が高くなる
という2点が既知であれば、年齢が処置(運動)と反応(コレステロール値)の両方の原因となる交絡因子になってしまっているということが説明できるわけです。そうであれば、やるべきことはただ一つ。図1.2を採用せず、図1.1を採用し、年齢層別のデータを用いて同年代同士で比べる、ということです。
冒頭に挙げたワクチンの重症化防止効果のデータも、年齢が「接種率」*8「(元々の)重症化傾向の強さ」*9の原因になってしまっていたことから、データ全体で見た場合に「効果なし」と見えていたのでしょう。これを10万人当たりの値(率)に換算し、さらにきちんと年齢層別にデータを分割すると「効果あり」という結論に到達するというわけです。
実際には本書のその後の箇所でも指摘されているように、必ずしもデータを分割すれば正しい結論に達するとは限らず、実はデータ全体で分析した方が正しい結論に至るケースもあります。ただし、そのようなケースでも適切に因果関係を整理して交絡因子を調整した結果として「データ全体で分析すべき」という結論になっています。その意味では「適切な因果推論さえ出来ていればデータを分割するにせよデータ全体を使うにせよ正しい結論に到達できるはず」とも言えます。
実務データ分析においてどう向き合うべきか
シンプソンのパラドックスとは、本質的にはWikipedia英語版の記事やPearl本でも指摘されているように「交絡因子の適切な調整で解決されるべきバイアス」なのでしょう。しかし、Pearl本が警告するように「データのみから因果関係を判別できるような統計的方法は存在しない」。つまり、シンプソンのパラドックスとは実は高度な因果推論的アプローチでなければ解決できない、意外と難易度の高い問題なんですね。
多くの統計学のテキストで挿話的にさらっと触れられることの多いシンプソンのパラドックスですが、これまで見てきたように因果推論の知識と交絡因子についての知識や情報がなければ正しい結論が存在することすら分からないわけで、冒頭に挙げたワクチンの重症化防止効果についても正しく解釈できなかった人が多かったのも無理からぬことかもしれません。
ただ、そのワクチンの効果に関するデータも、Pearl本で紹介されている例も、「年齢」がキーになっているという点が大きいと個人的には考えています。実際、公衆衛生や疫学に関するデータ分析の世界では「年齢」は交絡因子の定番中の定番とされているようです。それは、Pearl本の例にもあるように「処置」「反応」の両方に容易に影響を与えてしまうことが多いからなのでしょう。しかも、素朴に考えればそれは「健康」や「疾患」に限らない可能性があります。例えば世代ごとに「生活習慣」や「流行の事物」も異なることを考えれば、その交絡因子としての影響は無限に広がるのではないでしょうか。
それどころか、年齢の他にも交絡因子として影響の大きいものは世の中には色々存在するはずです。例えば、以前Rubinの傾向スコアを用いた事例として挙げた岩波DS3掲載の「TVCMがアプリゲーム利用時間に与える影響調査」のケースでは、何のバイアス調整も行わないと「TVCMを見れば見るほどゲーム時間が減る」という奇妙な結論に達してしまうのでした。この事例では「子供のいる世帯か否か」という交絡因子が強く影響しており、これを調整しない限り適切な結論には到達できなかったのです。
そういうわけで、広告・マーケティングなどの社会的データを扱う身としては、こういった交絡因子の存在を強く意識しながら適切にバイアスを補正していくことを忘れないようにしなければならないのだな、と自戒する次第です。「正しい因果推論は身を助く」ですね。
*1:コロナワクチンの副反応、ありましたか?に対するTakashi J. Ozakiさんの回答 - Quora
*2:何を書いているかはまだ秘密です
*3:後述するように特定の状況下では頻出するようですが
*4:http://math.bme.hu/~marib/bsmeur/simpson.pdf
*5:元の出典がJudea Pearlの2000年の論文なのであからさまに因果推論の文脈に置かれている感がありますが
*6:おそらく実測値ではなく下記の「常識」を踏まえて生成した数値例と思われる
*7:つまり交絡因子
*8:高齢者から優先して接種が進められていた
*9:高齢になるほど基礎体力や免疫機能が衰えるため
