(※はてなフォトライフの不具合で正しくない順番で画像が表示されている可能性があります)
だらだらと機械学習をパッケージで回していく様子を眺めるこのシリーズ、今回はロジスティック回帰をやってみようと思います。ロジスティック回帰はどちらかというとGLM(一般化線形モデル)なんですが、はじパタでもPRMLでも線形識別関数の1カテゴリとして取り上げているので、一応取り上げることに。
今回はごくごくありふれた機械学習と等価なGLMとしてのロジスティック回帰ということで、二値及び多項分類の場合のみ取り上げます。なお、ロジスティック回帰を含むGLMそのものについてはこの辺の過去記事を参照のこと。
- 今さら人に聞けない「重回帰分析の各手法の使い分け」 - 東京で働くデータサイエンティストのブログ*1
- 「使い分け」ではなく「妥当かどうか」が大事:重回帰分析&一般化線形モデル選択まわりの再まとめ - 東京で働くデータサイエンティストのブログ
一般的なGLMについて詳しく知りたい人は、例えばこの辺のテキストで勉強すると良いかもです。

- 作者: Annette J.Dobson,田中豊,森川敏彦,山中竹春,冨田誠
- 出版社/メーカー: 共立出版
- 発売日: 2008/09/08
- メディア: 単行本
- 購入: 15人 クリック: 152回
- この商品を含むブログ (13件) を見る
僕も持ってますが、なかなか読みやすいです。ちなみにロジスティック回帰ひとつとっても多項ロジットだけでなく二値変数・名義尺度・順序尺度のそれぞれのケースも取り上げている上に、GLMの一般論としてニュートン・ラフソン法で最尤推定するやり方の詳細まで載っている*2ので、GLMそのものについて知りたい人にはぴったりのテキストだと思います。
まずRでどんなものか見てみる
ひとまずロジスティック回帰の雰囲気だけ見たいので、GitHubに置いてある以前のサンプルデータを使いましょう。コンバージョン(CV)に効くアクション(a1-a7)を探り出そうというテーマで用意されたデータですね。これをdという名前でインポートしておきます。
以下に紹介してある計算自体は以前の記事と全く同じです。単にさっくりロジスティック回帰を計算して、偏回帰係数を出すだけです。
> d.glm<-glm(cv~.,d,family=binomial) > summary(d.glm) Call: glm(formula = cv ~ ., family = binomial, data = d) Deviance Residuals: Min 1Q Median 3Q Max -3.6404 -0.2242 -0.0358 0.2162 3.1418 Coefficients: Estimate Std. Error z value Pr(>|z|) (Intercept) -1.37793 0.25979 -5.304 1.13e-07 *** a1 1.05846 0.17344 6.103 1.04e-09 *** a2 -0.54914 0.16752 -3.278 0.00105 ** a3 0.12035 0.16803 0.716 0.47386 a4 -3.00110 0.21653 -13.860 < 2e-16 *** a5 1.53098 0.17349 8.824 < 2e-16 *** a6 5.33547 0.19191 27.802 < 2e-16 *** a7 0.07811 0.16725 0.467 0.64048 --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 (Dispersion parameter for binomial family taken to be 1) Null deviance: 4158.9 on 2999 degrees of freedom Residual deviance: 1044.4 on 2992 degrees of freedom AIC: 1060.4 Number of Fisher Scoring iterations: 7
これ自体は難しくも何ともありません。ここまではごくごく普通のGLMのお話です。ただ、以下に述べる「機械学習として見た場合のロジスティック回帰」の視点を持てるようになると、また面白く見えてくるんじゃないかと思います。
ロジスティック回帰とは何ぞや
細かいことは上に挙げた2つの過去エントリで既に紹介済みなんですが、もう一度おさらいしておきます。
統計学的には、これは上限と下限が定められていてxが正負どちらの∞に飛んで行ってもサチるような目的変数*3に対して、回帰を行うような方法論です。

これはロジット関数による変換を行い、最尤法で解くというものです(解析的には解けないのでニュートン-ラフソン法で解いたりMCMCで推定したりする)。ちなみにロジット関数でリンクした時の回帰式はこんな感じ。
一方、機械学習的に見た場合は区間[0,1]でクラス分類事後確率を求めるように線形識別関数*4を立てていくんですが、結局のところ同じような対数尤度関数ができるので、これを最急降下法とかニュートン-ラフソン法で解くことになります。要は、やってることはほとんど一緒です(笑)。
特に明示的にコードを書いて解く場合は『一般化線形モデル入門』pp.73-75に載っているような反復重み付き最小二乗法に則ってやるのが一般的なようです。ちなみに僕もその辺の実装は以前Matlabでやったことがありますが、その時に参考にしたのがこちらのブログ記事です。
ぶっちゃけこちらのPythonコードを組んで、挙動を見てもらった方が手っ取り早いんですが、それは今回の「パッケージのみで何とか済ませる」という趣旨に沿わないので悪しからず、ということでw
決定境界を描いてみる
さすがにこれは2次元データでないと辛いので、改めてGitHubにサンプルデータ1つ目、2つ目を上げておきました。それぞれdlogit1, dlogit2という名前でインポートしておきましょう。
dlogit1はオーソドックスな二値分類のケース、dlogit2は多項ロジットの3カテゴリ分類のケースを想定しています。まずは二値分類から見てみましょう。
> dlogit1$label<-as.factor(dlogit1$label) # labelをfactor型に直す > dlogit1.glm<-glm(label~.,dlogit1,family=binomial) # 普通に推定 > summary(dlogit1.glm) Call: glm(formula = label ~ ., family = binomial, data = dlogit1) Deviance Residuals: Min 1Q Median 3Q Max -2.18680 -0.19998 0.00022 0.14232 1.54751 Coefficients: Estimate Std. Error z value Pr(>|z|) (Intercept) -14.347 4.782 -3.000 0.0027 ** x 4.701 1.893 2.484 0.0130 * y 4.281 1.680 2.549 0.0108 * --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 (Dispersion parameter for binomial family taken to be 1) Null deviance: 69.315 on 49 degrees of freedom Residual deviance: 19.967 on 47 degrees of freedom AIC: 25.967 Number of Fisher Scoring iterations: 7 # 一応推定結果を見ておく > px<-seq(0,4,0.02) > py<-seq(0,5,0.02) > pgrid<-expand.grid(px,py) > names(pgrid)<-c("x","y") # グリッドを作る > plot(dlogit1[1:25,-3],pch=19,cex=3,col="red",xlim=c(0,3.5),ylim=c(0,3.5)) > points(dlogit1[26:50,-3],pch=19,cex=3,col="blue") > par(new=T) > contour(px,py,array(out.glm,dim=c(length(px),length(py))),xlim=c(0,3.5),ylim=c(0,3.5),col="purple",lwd=3,drawlabels=T,levels=0.5) # 決定境界を描く

という感じで、2つのクラスの間に綺麗に決定境界が引かれているのが分かります*5。偏回帰係数を見るとx, yともに有意になっていて、これらが決定境界を定めるのに有効であったということが分かります。
では、ロジスティック回帰のもう一つの特徴である多項ロジットによる3カテゴリ分類を見てみましょう。これは{VGAM}パッケージのvglm()関数を使う必要があります。
> install.packages("VGAM") # 中略 > require("VGAM") # 中略 > dlogit2$label<-as.factor(dlogit2$label) # labelをfactor型に直す > dlogit2.vglm<-vglm(label~.,dlogit2,family=multinomial) # vglm()で多項ロジットが計算できる > out.vglm<-predict(dlogit2.vglm,newdata=pgrid,type="response") # type="response"引数でクラス分類確率のマトリクスが出せる > out.vglm.class<-matrix(rep(0,dim(out.vglm)[1]),ncol=1) # この時点ではまだlength x 3のマトリクス > for (i in 1:length(out.vglm.class)) + { + out.vglm.class[i]<-as.numeric(which.max(out.vglm[i,]))-1 + } # 汚いfor文で恐縮ですが、0, 1, 2だけのクラス分類ベクトルに直す > plot(dlogit2[1:25,-3],pch=19,cex=3,col="red",xlim=c(0,4),ylim=c(0,5)) > points(dlogit2[26:50,-3],pch=19,cex=3,col="blue") > points(dlogit2[51:75,-3],pch=19,cex=3,col="green") > par(new=T) > contour(px,py,array(out.vglm.class,dim=c(length(px),length(py))),xlim=c(0,4),ylim=c(0,5),col="purple",lwd=3,drawlabels=T,levels=c(0,1,2)) # 決定境界を描く

という感じで、綺麗に3つのクラスの間にそれぞれ決定境界が引かれているのが分かると思います。多項ロジットは多クラス分類では割と一般的に使われる手法なので、覚えておいて損はないです。
注意点
想像がついた人もいると思いますが、これは基本的には「多クラス分類にも使える線形識別関数」なので、非線形になると全く使えません*6。なので、例えばXORパターンに当てはめてやると悲惨なことになります。
前回の記事で使ったXORパターンのデータを、xorという名前でインポートして、こうしてみます。
> xor$label<-as.factor(xor$label-1) # labelをfactor型に直す > xor[,-3]<-xor[,-3]+2 # 便宜上平行移動させておく > xor.glm<-glm(label~.,xor,family=binomial) > out.xor.glm<-predict(xor.glm,newdata=pgrid) # 推定して予測グリッドを作る > plot(xor[1:50,-3],pch=19,cex=3,col="red",xlim=c(0,4),ylim=c(0,5)) > points(xor[51:100,-3],pch=19,cex=3,col="blue") > par(new=T) > contour(px,py,array(out.xor.glm,dim=c(length(px),length(py))),xlim=c(0,4),ylim=c(0,5),col="purple",lwd=3,drawlabels=T,levels=c(0,1) # 決定境界を描画する
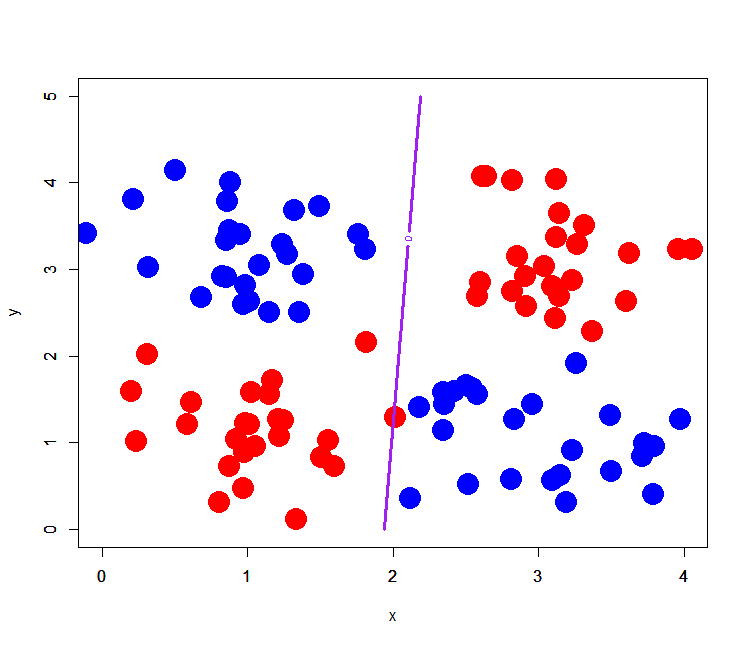
おいおいウソこけよ、どこ分類してるんじゃーーー!!! ということで、普通にロジスティック回帰しても線形分離不可能パターンは分類できないという点に注意が必要です。そういう時は非線形分離が可能な他の手法*7を選ぶ必要があるというわけですね。
ちなみに念のため偏回帰係数を見ると、
> summary(xor.glm) Call: glm(formula = label ~ ., family = binomial, data = xor) Deviance Residuals: Min 1Q Median 3Q Max -1.25789 -1.16189 -0.00116 1.16965 1.26498 Coefficients: Estimate Std. Error z value Pr(>|z|) (Intercept) 0.200178 0.571918 0.350 0.726 x -0.103236 0.177324 -0.582 0.560 y 0.005144 0.176762 0.029 0.977 (Dispersion parameter for binomial family taken to be 1) Null deviance: 138.63 on 99 degrees of freedom Residual deviance: 138.29 on 97 degrees of freedom AIC: 144.29 Number of Fisher Scoring iterations: 3
となっていて、xもyも説明変数としてはアウトという判定になっています。そりゃ線形分離不可能だから仕方ないんですが。。。線形分離可能な説明変数のみが、有意になるというのがロジスティック回帰のポイントというわけです。