前回の記事からだいぶ経ってしまいましたが、皆様パッケージの使い心地はいかがでしょうか(汗)。ということで、今回はいよいよクラスタリングシリーズの大詰め、混合ディリクレ過程を取り上げます。
今回は僕も完全に理解しているわけではないので、ぶっちゃけこんなブログ記事読まずにもっとちゃんとした方の資料を読んでもらった方が100倍以上皆さんのためになると思いますorz 特に日本語資料がほとんどないということで結構大変なんですが、@shima__shima先生に伺ったところこんなお答えが。
.@TJO_datasci ノンパラはガッツリ書いてるのをあまり見かけません.持橋さんの資料とか http://t.co/9Yuv1DpIdp 吉井さんのとか https://t.co/KC8t94wBzo
— しましま (@shima__shima) 2014, 4月 14
ちなみにどちらもPDFなので要注意。そして僕もこれを読んだからといって何か理解が大きく進んだというわけでもないので(泣)、ぜひぜひ皆さん自身で読み込んでみてください。。。
まずRでどんなものか見てみる
実は{DPpackage}で3変数以上でやる方法が分からないので、割愛しますorz ごめんなさい。。。むしろ詳しい人ぜひぜひぜひぜひ僕に教えて下さい~~~~~~m(_ _)m*1
混合ディリクレ過程とは何ぞや
もちろん僕も生半可を通り越してほとんど分かっていないので知ったかぶりすら出来ない状況なんですが、上記の資料を読んだり色々な人に教えてもらった内容を簡単にまとめるとこんな感じでしょうか。
- ディリクレ分布は多項分布の共役事前分布で、例えばクラスタ「数」を表現するのに適している
- ディリクレ過程は、ディリクレ分布を無限次元に拡張したもので、例えばクラスタ「数」を無限に多く推定することができる
- そしてディリクレ過程に従えば、頻度が高いものほどさらに現れやすくなる(Chinese Restaurant Process: 中華レストラン過程*2)
- そこでこれをEMアルゴリズムによる混合モデルの時と同様に、ディリクレ過程を混合させたものを仮定する(混合ディリクレ過程)
- 以上を合わせて、クラスタに分けられるデータ要素の確率のみならず、クラスタ「数」自体の事後分布を求めることで、クラスタ「数」すらも推定する
色々抜けてたり解釈が間違ってるところがありそうなので、突っ込んでいただけると有難いですorz ともあれ、この一連の枠組みをノンパラメトリック・ベイズ法(ノンパラベイズ)と称するようです。その中のひとつが、混合ディリクレ過程(Dirichlet Process Mixture: DPM)という。
細かい理屈は山ほどありますが、DPMのポイントは「クラスタ数をも推定できる」ということ。ただしこれは後で見るように吉と出ることもあれば凶と出ることもあるので、色々注意が必要です。
真の分布の分かっているデータをクラスタリングしてみる
相変わらず3変数以上のデータへのDPMのやり方は分からないので、2変数で済む2次元XORパターンでやってみましょう。GitHubからシンプルパターンだけ落としてきてdという名前でインポートしてください。
用いるのは{DPpackage}パッケージです。これはディリクレ過程にまつわる関数を多く実装しているパッケージで、今回はDPdensity()を使います。以下はDPdensity()のヘルプから一部を改変しただけの超シンプルなRコード例です。
> d <- read.table("~/Dev/R/Blog/xor_simple.txt", header=T, quote="\"") > d<-d[,-3] > # Prior information > > s2 <- matrix(c(10000,0,0,1),ncol=2) > m2 <- c(180,3) > psiinv2 <- solve(matrix(c(10000,0,0,1),ncol=2)) > > prior <- list(a0=1,b0=1/10,nu1=4,nu2=4,s2=s2, + m2=m2,psiinv2=psiinv2,tau1=0.01,tau2=0.01) > > # Initial state > state <- NULL > > # MCMC parameters > > nburn <- 5000 > nsave <- 10000 > nskip <- 10 > ndisplay <- 1000 > mcmc <- list(nburn=nburn,nsave=nsave,nskip=nskip,ndisplay=ndisplay) > > # Fit the model > fit1 <- DPdensity(d,prior=prior,mcmc=mcmc, + state=state,status=TRUE,na.action=na.omit) MCMC scan 1000 of 10000 (CPU time: 16.786 s) MCMC scan 2000 of 10000 (CPU time: 25.569 s) MCMC scan 3000 of 10000 (CPU time: 36.067 s) MCMC scan 4000 of 10000 (CPU time: 46.363 s) MCMC scan 5000 of 10000 (CPU time: 60.263 s) MCMC scan 6000 of 10000 (CPU time: 73.898 s) MCMC scan 7000 of 10000 (CPU time: 81.495 s) MCMC scan 8000 of 10000 (CPU time: 96.315 s) MCMC scan 9000 of 10000 (CPU time: 106.673 s) MCMC scan 10000 of 10000 (CPU time: 115.300 s) > fit1$state$ss [1] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 1 1 1 1 1 1 [32] 1 1 1 1 1 4 1 1 5 1 1 1 1 1 1 1 1 1 1 6 4 6 4 4 4 4 4 4 4 4 4 [63] 4 4 6 4 4 4 4 4 4 1 4 4 4 2 5 5 5 2 2 5 5 5 5 5 5 2 2 2 5 5 5 [94] 2 2 5 5 5 5 2 > plot(d,col=fit1$state$ss,pch=19,cex=3)
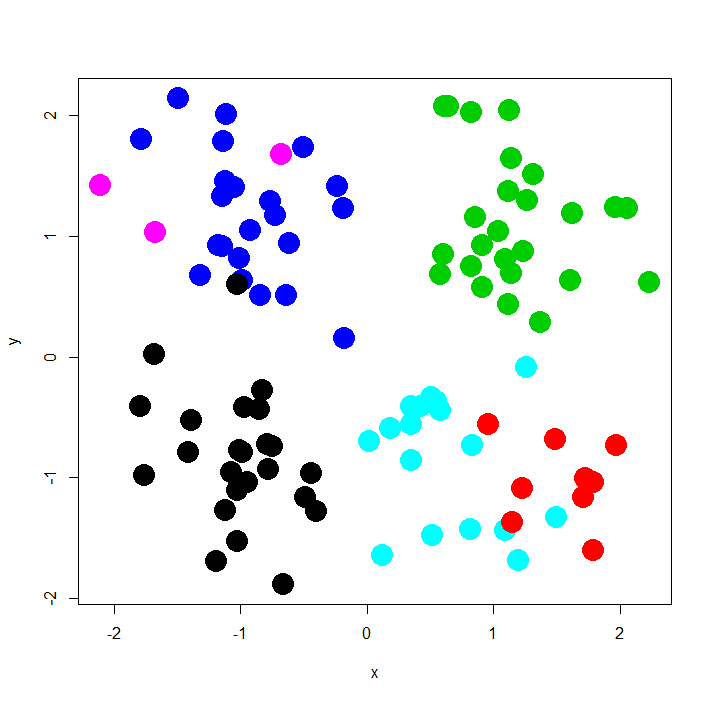
あれ、何故か真のクラスタ数は4個のはずなのに、6個になっちゃってますね。実はこの点については昨年末のNIPS2013で興味深い発表(A simple example of Dirichlet process mixture inconsistency for the number of components)がなされていて、曰く「DMPはごくごく小さなクラスタとして判定され得るような微妙なデータがあるとほぼ必然的にそれをクラスタリングしてしまい、結果として全体のクラスタリングにも影響を与え、真のクラスタ数よりも最終的に多いクラスタ数を推定してしまうことがある」とのこと。
そんなわけで、クラスタ数まで全部自動で推定してくれるから楽チン!とか思ってるとドツボにハマる可能性があるので気を付けましょうということで。。。ちなみに今回はXORの複雑パターンについては割愛しました。何故なら、クラスタ数「1」(=クラスタリング不能)とどうあがいても判定されてしまうのでorz この辺も詳しい人是非教えていただきたいです。。。
最後に
一応affinity propagationが{apcluster}でRでは実装されているので、そこぐらいまではやろうかなぁと思ってます。。。ってかいつまでやるんだこれ。