だいぶ食傷気味の方も多いかもしれませんが、懲りずに今回もMMM (Marketing/Media Mix Modeling)ネタをやります。この度取り上げるのはこちらです。
そう、PyMC Marketing MMMです。あくまでも僕の観測範囲ですが、広く普及しているPyMCベースなのもあってか、群雄割拠するMMMライブラリの中でも比較的広く支持を集めているように見受けられます。
MMMは歴史の長いマーケティング分析手法で、その実装方法もそれに応じて多岐に渡りますが、近年ではJin et al. (2017)に準拠したベイジアンMMMが主流になりつつようです*1。そのオリジナル実装は僕の勤務先では社内版として利用できますが、それをJAX + NumPyroで再実装したのがLightweight MMM*2、そしてそこに色々なコンポーネントを追加して全面的にTensorFlow Probabilityで実装し直したのがMeridianです。
なのですが、先日の記事でも触れた通りMeridianには既存実装には見られない独特のfeatureが多く、時にはユーザーを困惑させることもあるようです。このためJin et al. (2017)により忠実な実装を求める声も少なくないようで、その代表格としてPyMC Marketing MMMが挙げられることもまた多いと伝え聞いています。
ということで、今回の記事ではそのPyMC Marketing MMMがどんなものかを公式のEnd-to-End Case Studyをなぞりながらレビューしてみようと思います。なお、今回ご紹介するコードは独立に取得した実データに対しても回ることを確認していますが、後述する事情もあり、芸がないのは承知の上で配布元指定のオープンデータを用いています。
PyMC Marketing MMMの標準的な実行コード
以下にPyMC Marketing MMM公式のEnd-to-End StudyをなぞったColab向け実行コードを並べておきます。全て取り上げるとかなり長くなってしまうので、冗長と思われるパートは割愛しました。なお、そのままコピペするとtypoやモジュール構造参照の誤りなどでエラーを吐いてコケるので、僕の判断でデバッグしてあります。
インストール&インポート
!pip install git+https://github.com/pymc-labs/pymc-marketing.git
普通にGitHub経由でpipで入ります。
import warnings import arviz as az import matplotlib.pyplot as plt import numpy as np import pandas as pd import seaborn as sns from pymc_marketing.metrics import crps from pymc_marketing.mmm import MMM, GeometricAdstock, LogisticSaturation from pymc_marketing.mmm.utils import apply_sklearn_transformer_across_dim # from pymc_marketing.prior import Prior # コケる from pymc_extras.prior import Prior warnings.filterwarnings("ignore", category=FutureWarning) az.style.use("arviz-darkgrid") plt.rcParams["figure.figsize"] = [12, 7] plt.rcParams["figure.dpi"] = 100 seed: int = sum(map(ord, "mmm")) rng: np.random.Generator = np.random.default_rng(seed=seed)
インポートも簡単です。なおJuPyter Notebook向けのコードブロックは割愛しました。
データ準備
raw_df = pd.read_csv("https://raw.githubusercontent.com/sibylhe/mmm_stan/main/data.csv") # 1. control variables # We just keep the holidays columns control_columns = [col for col in raw_df.columns if "hldy_" in col] # 2. media variables channel_columns_raw = [ col for col in raw_df.columns if "mdsp_" in col and col != "mdsp_viddig" and col != "mdsp_auddig" and col != "mdsp_sem" ] channel_mapping = { "mdsp_dm": "Direct Mail", "mdsp_inst": "Insert", "mdsp_nsp": "Newspaper", "mdsp_audtr": "Radio", "mdsp_vidtr": "TV", "mdsp_so": "Social Media", "mdsp_on": "Online Display", } channel_columns = list(channel_mapping.values()) # 3. sales variables sales_col = "sales" data_df = raw_df[["wk_strt_dt", sales_col, *channel_columns_raw, *control_columns]] data_df = data_df.rename(columns=channel_mapping) # 4. Date column data_df["wk_strt_dt"] = pd.to_datetime(data_df["wk_strt_dt"]) date_column = "wk_strt_dt"
データはPyMC Marketingが指定している公開のMMMサンプルデータを用います。若干煩雑なデータセットなので多少の前処理が必要です。
fig, ax = plt.subplots() sns.lineplot(data=data_df, x=date_column, y="sales", color="black", ax=ax) ax.set(title="Sales", xlabel="date", ylabel="sales");

目的変数である"Sales"をプロットするとこんな感じになります。
fig, ax = plt.subplots() data_df.set_index("wk_strt_dt")[channel_columns].plot(ax=ax) ax.legend(title="Channel", fontsize=12) ax.set(title="Media Spend", xlabel="Date", ylabel="Spend");
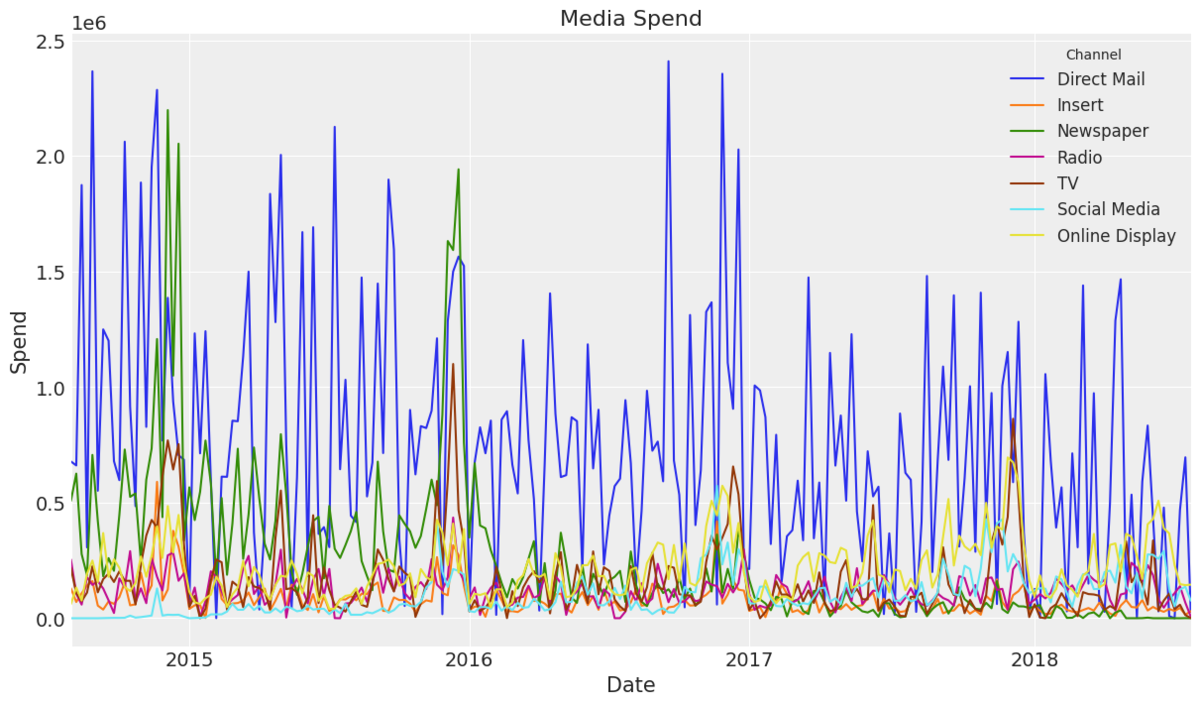
メディア変数を重ねてプロットするとこんな感じです。普段からMMMを回している人であれば、ここでもう下馬評が立てられるかと思います。
train_test_split_date = pd.to_datetime("2018-02-01") train_mask = data_df.wk_strt_dt <= train_test_split_date test_mask = data_df.wk_strt_dt > train_test_split_date train_df = data_df[train_mask] test_df = data_df[test_mask] X_train = train_df.drop(columns=sales_col) X_test = test_df.drop(columns=sales_col) y_train = train_df[sales_col] y_test = test_df[sales_col] fig, ax = plt.subplots() sns.lineplot(data=train_df, x="wk_strt_dt", y="sales", color="C0", label="Train", ax=ax) sns.lineplot(data=test_df, x="wk_strt_dt", y="sales", color="C1", label="Test", ax=ax) ax.set(title="Sales - Train Test Split", xlabel="date");

データ全体をtrain/testにsplitします。分割方式は標準的なpast-and-future splitです。
spend_shares = (
X_train.melt(value_vars=channel_columns, var_name="channel", value_name="spend")
.groupby("channel", as_index=False)
.agg({"spend": "sum"})
.sort_values(by="channel")
.assign(spend_share=lambda x: x["spend"] / x["spend"].sum())["spend_share"]
.to_numpy()
)
prior_sigma = spend_shares
メディア費用とその比率を出しておきます。後者はメディア回帰係数の事前分布に用いられます。
モデル設定&MCMCサンプリング
model_config = {
"intercept": Prior("Normal", mu=0.2, sigma=0.05),
"saturation_beta": Prior("HalfNormal", sigma=prior_sigma, dims="channel"),
"saturation_lam": Prior("Gamma", alpha=3, beta=1, dims="channel"),
"gamma_control": Prior("Normal", mu=0, sigma=1),
"gamma_fourier": Prior("Laplace", mu=0, b=1),
"likelihood": Prior("Normal", sigma=Prior("HalfNormal", sigma=0.5)),
}
各種事前分布を設定します。メディア回帰係数にはオーソドックスな半正規分布を充てています。
sampler_config = {"progressbar": True}
mmm = MMM(
model_config=model_config,
sampler_config=sampler_config,
date_column=date_column,
adstock=GeometricAdstock(l_max=6),
saturation=LogisticSaturation(),
channel_columns=channel_columns,
control_columns=control_columns,
yearly_seasonality=5,
)
MMMのオブジェクトを立てます。yearly_sesonality引数が5である理由は僕には読み取れませんでした。
# Generate prior predictive samples mmm.sample_prior_predictive(X_train, y_train, samples=4_000) fig, ax = plt.subplots() fig = mmm.plot_prior_predictive(original_scale=True, ax=ax) ax.legend(loc="lower center", bbox_to_anchor=(0.5, -0.2), ncol=4) ax.set(xlabel="date", ylabel="sales");
事前分布サンプルのチェックもできます。プロットは割愛。
try: import numpyro # noqa: F401 nuts_sampler = "numpyro" except ModuleNotFoundError: nuts_sampler = "pymc" mmm.fit( X=X_train, y=y_train, target_accept=0.9, chains=4, draws=3_000, nuts_sampler=nuts_sampler, random_seed=rng, )

MCMCサンプリングを回します。後述しますが、PyMCなせいか微妙に回るのが遅い気がします……。
モデル診断
az.summary(
data=mmm.idata,
var_names=[
"intercept",
"y_sigma",
"saturation_beta",
"saturation_lam",
"adstock_alpha",
"gamma_control",
"gamma_fourier",
],
)["r_hat"].describe()

R_hatを確認しておきます。全部1.0のようです。
_ = az.plot_trace(
data=mmm.fit_result,
var_names=[
"intercept",
"y_sigma",
"saturation_beta",
"saturation_lam",
"adstock_alpha",
"gamma_control",
"gamma_fourier",
],
compact=True,
backend_kwargs={"figsize": (12, 10), "layout": "constrained"},
)
plt.gcf().suptitle("Model Trace", fontsize=16);

MCMCサンプルのトレースプロットを見てみます。問題なさそうです。
mmm.sample_posterior_predictive(X_train, extend_idata=True, combined=True) fig = mmm.plot_posterior_predictive(original_scale=True) fig.gca().set(xlabel="date", ylabel="sales");

学習データへの当てはまりをプロットします。悪くないように見えます。
y_pred_test = mmm.sample_posterior_predictive(
X_pred=X_test,
include_last_observations=True,
original_scale=True,
var_names=["y", "channel_contribution"],
extend_idata=False,
progressbar=False,
random_seed=rng,
)
fig, ax = plt.subplots()
mmm.plot_posterior_predictive(original_scale=True, ax=ax)
test_hdi_94 = az.hdi(y_pred_test["y"].to_numpy().T, hdi_prob=0.94)
test_hdi_50 = az.hdi(y_pred_test["y"].to_numpy().T, hdi_prob=0.50)
ax.fill_between(
X_test[date_column],
test_hdi_94[:, 0],
test_hdi_94[:, 1],
color="C1",
label=f"{0.94:.0%} HDI (test)",
alpha=0.2,
)
ax.fill_between(
X_test[date_column],
test_hdi_50[:, 0],
test_hdi_50[:, 1],
color="C1",
label=f"{0.50:.0%} HDI (test)",
alpha=0.4,
)
ax.plot(X_test[date_column], y_test, color="black")
ax.plot(
X_test[date_column],
y_pred_test["y"].mean(dim="sample"),
color="C1",
linewidth=3,
label="Posterior Predictive Mean",
)
ax.axvline(X_test[date_column].iloc[0], color="C2", linestyle="--")
ax.legend(loc="upper center", bbox_to_anchor=(0.5, -0.1), ncol=4)
ax.set(ylabel="sales");

学習データ・テストデータそれぞれへの当てはまりをプロットします。見た感じ問題なさそうです。
fig, ax = plt.subplots()
ax.fill_between(
X_test[date_column],
test_hdi_94[:, 0],
test_hdi_94[:, 1],
color="C1",
label=f"{0.94:.0%} HDI (test)",
alpha=0.2,
)
ax.fill_between(
X_test[date_column],
test_hdi_50[:, 0],
test_hdi_50[:, 1],
color="C1",
label=f"{0.50:.0%} HDI (test)",
alpha=0.4,
)
ax.plot(X_test[date_column], y_test, marker="o", color="black", label="Observed")
ax.plot(
X_test[date_column],
y_pred_test["y"].mean(dim="sample"),
marker="o",
markersize=8,
color="C1",
linewidth=3,
label="Posterior Predictive Mean",
)
ax.legend(loc="upper center", bbox_to_anchor=(0.5, -0.1), ncol=4)
ax.set(title="Out-of-Sample Predictions", xlabel="date", ylabel="sales");

テストデータだけ拡大してプロットしてみるとこんな感じです。微妙にずれている気もしますが、大体信用区間に収まっているので良しとしましょう。
メディア効果の評価
fig = mmm.plot_direct_contribution_curves() [ax.set(xlabel="spend") for ax in fig.axes]; mmm.plot_channel_contribution_grid(start=0, stop=1.5, num=12, figsize=(15, 7));’ mmm.plot_channel_contribution_grid( start=0, stop=1.5, num=12, absolute_xrange=True, figsize=(15, 7) );
Response curveですが、3通りの可視化手法が例示されています。プロットは冗長なので割愛しました。
fig = mmm.plot_channel_contribution_share_hdi(figsize=(10, 6)) fig.suptitle("Channel Contribution Share", fontsize=18, fontweight="bold");
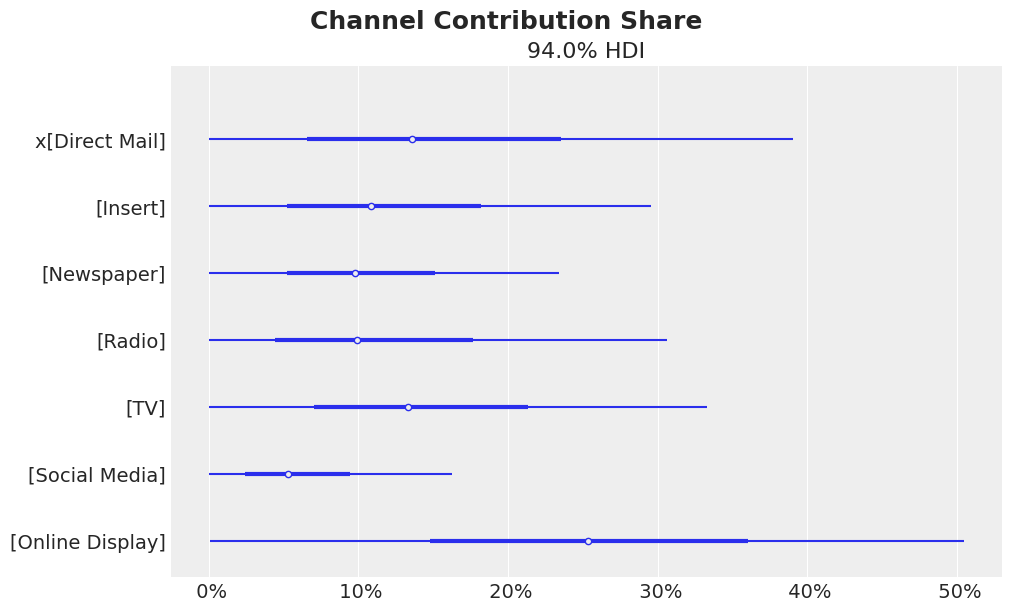
メディアごとの寄与度をプロットします。
# Get the channel contributions on the original scale channel_contribution_original_scale = mmm.compute_channel_contribution_original_scale() # Sum the contributions over the whole training period spend_sum = X_train[channel_columns].sum().to_numpy() spend_sum = spend_sum[ np.newaxis, np.newaxis, : ] # We need these extra dimensions to broadcast the spend sum to the shape of the contributions. # Compute the ROAS as the ratio of the mean contribution and the spend for each channel roas_samples = channel_contribution_original_scale.sum(dim="date") / spend_sum # Plot the ROAS fig, ax = plt.subplots(figsize=(10, 6)) az.plot_forest(roas_samples, combined=True, ax=ax) fig.suptitle("Return on Ads Spend (ROAS)", fontsize=18, fontweight="bold");
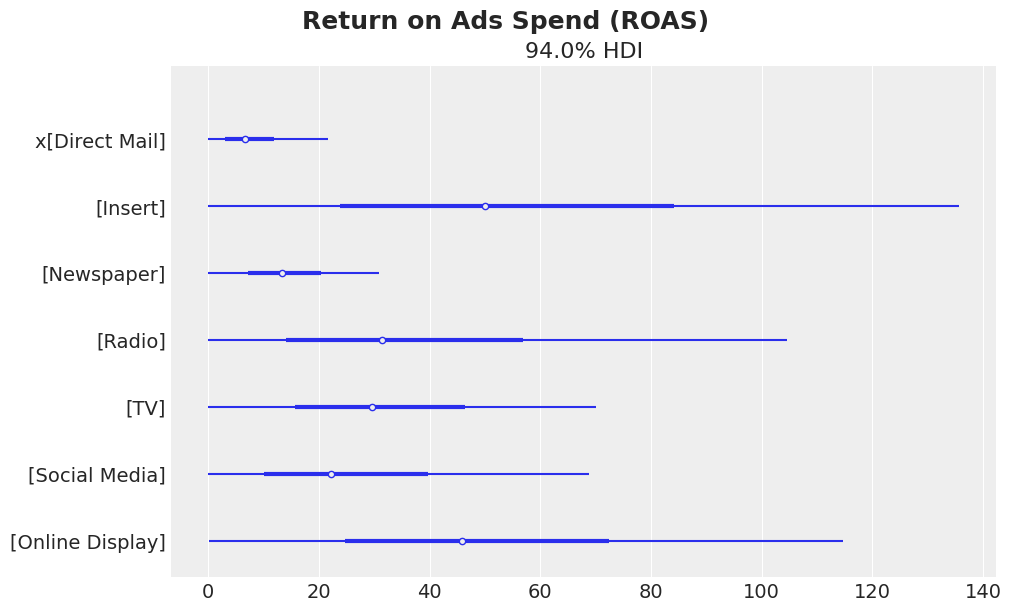
ROASをプロットします。
予算配分の最適化
num_periods = X_test[date_column].shape[0] # Total budget for the test set per channel all_budget_per_channel = X_test[channel_columns].sum(axis=0) # Total budget for the test set all_budget = all_budget_per_channel.sum() # Weekly budget for each channel # We are assuming we do not know the total budget allocation in advance # so this would be the naive "uniform" allocation. per_channel_weekly_budget = all_budget / (num_periods * len(channel_columns))
average_spend_per_channel_train = X_train[channel_columns].sum(axis=0) / ( X_train.shape[0] * len(channel_columns) ) average_spend_per_channel_test = X_test[channel_columns].sum(axis=0) / ( X_test.shape[0] * len(channel_columns) )
percentage_change = 0.5 mean_spend_per_period_test = ( X_test[channel_columns].sum(axis=0).div(num_periods * len(channel_columns)) ) budget_bounds = { key: [(1 - percentage_change) * value, (1 + percentage_change) * value] for key, value in (mean_spend_per_period_test).to_dict().items() }
model_granularity = "weekly" allocation_strategy, optimization_result = mmm.optimize_budget( budget=per_channel_weekly_budget, num_periods=num_periods, budget_bounds=budget_bounds, minimize_kwargs={ "method": "SLSQP", "options": {"ftol": 1e-9, "maxiter": 5_000}, }, ) response = mmm.sample_response_distribution( allocation_strategy=allocation_strategy, time_granularity=model_granularity, num_periods=num_periods, noise_level=0.05, )
予算配分の最適化計画を回します。
fig, ax = plt.subplots()
(
pd.Series(allocation_strategy, index=mean_spend_per_period_test.index)
.to_frame(name="optimized_allocation")
.join(mean_spend_per_period_test.to_frame(name="initial_allocation"))
.sort_index(ascending=False)
.plot.barh(figsize=(12, 8), color=["C1", "C0"], ax=ax)
)
ax.set(title="Budget Allocation Comparison", xlabel="allocation");

予算配分を現状と最適化後とで並べてプロットします。
End-to-End Case Studyを初めとして、公式サイトでは他にも様々な分析やプロットのコードが例示されていますので、ここで紹介しなかった箇所に興味のある方は是非ご自身で当該ページをご参照ください。
特徴的なポイント
あくまでも僕個人が一通り触ってみての感想と公式ページの記述を踏まえてのものにはなりますが、PyMC Marketing MMMの特徴的なポイントを一通り挙げておきます。
現行のMMMライブラリの中では最もJin et al. (2017)に忠実
Jin et al. (2017)については8年前にもこのブログでちょろっと取り上げていまして、記事中でも参照したように他所様のブログでも詳細に解説されているのでそちらも是非お読みいただきたいのですが*3、端的に言って現行のMMMライブラリの中ではPyMC Marketing MMMが最もこの論文に忠実と言って良いかと思います。勿論、忠実であることが本当に良いか悪いかというと議論のある部分かとは思いますが、少なくとも「多くの人々が考えるベイジアンMMM」に近いとは言えそうです。
一方で現代的なMMMということで因果推論も意識した構成になっており、わざわざ未観測交絡因子や反実仮想モデリングといった話題をカバーしたケーススタディまで用意してある点は特筆に値すると思います。
トレンド・季節調整はオーソドックスな推定を行っている
MMMというか時系列モデルに付きもののトレンドと季節調整ですが、PyMC Maraketing MMMでは前者は(ローカル)線形トレンドで、後者はフーリエ変換で、それぞれオーソドックスなやり方で推定しています。ただしオプションとしてガウス過程回帰も用意しているようですし、因果推論における調整変数導入の文脈でもガウス過程回帰の話題が出てくるのですが、未見なので論評は差し控えます。
交差検証は標準的なpast-and-future splitを採っている
線形トレンド推定でトレンドを捉えているということで、上述した実行コード例で見た通り、交差検証方式も時系列モデルでは標準的な「未来予測性能」を重視したpast-and-future splitを採用しています。
ちなみに一手間かければ、時系列モデルのロバスト性を見るための交差検証方式であるtime slice (sliding time window) CVも使えます。時間とリソースに余裕がある場合はこちらでも良いと思います。
予算配分最適化はオリジナルと同じ逐次二次計画法を用いている
実行コード例に"SLSQP"の語が見える通りで、予算配分の最適化計画にはJin et al. (2017)で提案されているのと同様に逐次二次計画法が用いられています。Meridian以下近年の実装はグリッドサーチを採用しているものが多いので、貴重かも?
利用する上での注意点
これまた僕個人が手元で試してみての感想&公式の資料を読んでみての考察ではありますが、PyMC Marketing MMMを利用する上での注意点についても以下に記しておきます。
PyMCなせいかMCMC含めてサンプリングを伴う処理が遅い気がする
これは僕の偏見に過ぎない可能性がありますが、PyMCベースなせいかMCMC含めてサンプリングが遅い気がしています。本チャンのモデル推定だけならまだしも、メディア効果の推定などでもちょっと時間がかかる印象があります。
で、ググってみたらこんなforum issueを見つけました。もしかしたら高速化のための手続的処理が必要なんですかね?
低レベルAPIが主なので細かいところの実装が割と面倒
どちらかというとこれはMeridianとの比較になりますが、ちょっとした可視化プロットにも毎回matplotlibでゴリゴリ書かなければならないのを筆頭に、train/test splitや予算配分最適化のところも含めて、MMM「ライブラリ」と言いながら自分で色々とコードを書かなければいけないパートが多い気がしています。言い換えると、Meridianなら高レベルAPIで1行書けば終わりのところを、PyMC Marketing MMMでは低レベルAPIでオブジェクトを作った後は全部自前で書いていく必要がある、という感じです。
実はこれは上記リンクの通りPyMC Marketing公式でも自ら認めている話で、そこを逆手に取っているわけではないのでしょうが「最大限カスタマイズできるのが強み」とまで言っています。まぁ確かにMMMというと独自に魔改造したい事業者が多いので、それでもいいんですかね……。
交絡の調整変数は単純に線形回帰項として追加されるだけに見える
Meridianだと交絡の調整変数はChen et al. (2018)に基づいてスプライン回帰としてモデルに組み込まれますが(これが理由でベースライン・トレンド・季節調整の推定と調整変数の導入が全てごっちゃにされている感がある)、PyMC Marketing MMMではどのように対応しているかがはっきりしません。上記リンクの通り未観測交絡因子をガウス過程回帰で捉えるという話題は出てくるものの、調整変数(特に上流)が手に入る場合の対処の話が見当たらないのです。
モデル式の記述でも特に触れられていないのとベースライン・トレンド・季節調整が別建てになっているところを見るに、恐らく調整変数は単純に線形回帰項として追加されるだけなのではないかと推測しています。勿論、それが「正しい」かどうかはまた別の議論です*4。
メディア回帰係数の事前分布を半正規分布以外に変えて収束するかどうかは不明
Jin et al. (2017)準拠ということでPyMC Marketing MMMはメディア回帰係数の事前分布を半正規分布に設定していますが、Meridianではゼロ点付近にMCMCサンプルの最頻値が寄りがちな傾向を考慮して対数正規分布に設定しています*5。
個人的には対数正規分布の方が「非負」「ゼロ点付近に手厚い」の2条件を満たしていて好ましいと考えていて、PyMC Marketing MMMでもその方が良いのではないかと思うのですが……実はあるデータセットに対してPyMC Marketing MMMでモデリングした際にメディア回帰係数の事前分布を対数正規分布(LogNormal)に変更してみたことがあるのですが、MCMCサンプリングが収束しなかったのでした。ただ、そのデータセット自体が不適切だったのか、実際にLogNormalだとダメなのかの検証はまだしていないので、結論は出ていません。ここでは一旦「不明」としておきます。
コメントなど
実はMeridianとの比較という文脈で今回PyMC Marketing MMMの調査を始めたんですが、Meridian提供のサンプルデータを読み込ませてPyMC Marketing MMMを回すとMCMCが収束しない一方、PyMC Marketing MMM側が生成した別のサンプルデータを読み込ませてMeridianを回してもやはりMCMCが収束しないんですね(汗)。お互いに事前分布をチューニングし倒した上でそれに合わせてサンプルデータを生成させているんだろうなぁと感じさせられた一幕でした。
ちなみに、独立に取得した実データに対してはPyMC Marketing MMMもMeridianも綺麗にMCMCが収束するので、その辺は安心して良さそうです。なので本音を言えばその実データを使った結果を今回の記事でもお見せしたかったんですが、そもそも実データの提供元からの許諾が得られていないので断念しました……MMMの技術的探求は難しいですね。
余談ながら。実はPyMC Labsの公式記事としてPyMC Marketing MMMとMeridianの技術的優劣を論じた記事が出ていて、まぁ予想通りですが「PyMC Marketing MMMの方がMeridianより優れている」という結果になっています(苦笑)。僕自身の立場*6としてはそれに同意するわけにはいかないのですが、あくまでも技術的な思想の違いという観点から「両者を使い分ける」こと自体はあっても良いのかなと考えています。
*2:今年1月でメンテ終了
*3:特にこちら:読書日記: 読了: Jin, Wang, Sun, Chan, Koehler (2017) これが俺らのマーケティング・ミックス・モデル (lyric by Google AI) / 読書日記 | 読んだ本を淡々と記録します
*4:実は上記論文の筆頭著者に「ベイジアンMMMでも調整変数項がスプライン回帰である必要はあるのか」と聞いたんですが、「試したことがないので知らん」という回答が返ってきたのでした
*5:非負制約を嵌めている一方で「効果ゼロ」に推定結果が寄りやすいため
*6:Conflict of interests: 筆者はMeridian配布元の企業に所属しています