去る2月5日(木)にレバレジーズ様のお招きで渋谷でちょっとしたRハンズオンをやってきました。
この中で利用したのが、UCI Machine Learning Repositoryのオープンデータセット。恥ずかしながら僕は最近になってこのリポジトリの存在を知ったんですが、結構な老舗の割に今でも頻繁に更新されていて、つい最近もNoisyOfficeというデータセットが追加されたばかりのようです。
で、上記Rハンズオンの中で題材に取り上げたデータのひとつがTennis Major Tournament Match Statistics。これは2013年のプロテニスの四大大会のmatch statsをATP / WTA双方について集めたもので、おそらくIBMとかOMEGAとかRADO辺りが公開しているものではないかと思います。実業団リーグにも参加していたことのあるテニス好きの僕としてはこれほど面白いデータもないということで取り上げさせていただいたんですが、時間の都合もありUSオープンのデータしか用いませんでした。
ということで、その補遺も兼ねて4大会全てのデータを使って以下機械学習のお遊びということでやってみようと思います。
データセット
面倒なので4大会分男女別にまとめたものをGitHubに置いておきました。men.txtとwomen.txtをそれぞれDLしてきて、データフレームdm, dwとして読み込んでください。
いくつか変数を取捨選択してあるので全部が揃っているわけではないんですが、元のページを見ると変数について以下のように説明があります。
Player 1 Name of Player 1
Player 2 Name of Player 2
Result Result of the match (0/1) - Referenced on Player 1 is Result = 1 if Player 1 wins (FNL.1>FNL.2)
FSP.1 First Serve Percentage for player 1 (Real Number)
FSW.1 First Serve Won by player 1 (Real Number)
SSP.1 Second Serve Percentage for player 1 (Real Number)
SSW.1 Second Serve Won by player 1 (Real Number)
ACE.1 Aces won by player 1 (Numeric-Integer)
DBF.1 Double Faults committed by player 1 (Numeric-Integer)
WNR.1 Winners earned by player 1 (Numeric)
UFE.1 Unforced Errors committed by player 1 (Numeric)
BPC.1 Break Points Created by player 1 (Numeric)
BPW.1 Break Points Won by player 1 (Numeric)
NPA.1 Net Points Attempted by player 1 (Numeric)
NPW.1 Net Points Won by player 1 (Numeric)
TPW.1 Total Points Won by player 1 (Numeric)
ST1.1 Set 1 result for Player 1 (Numeric-Integer)
ST2.1 Set 2 Result for Player 1 (Numeric-Integer)
ST3.1 Set 3 Result for Player 1 (Numeric-Integer)
ST4.1 Set 4 Result for Player 1 (Numeric-Integer)
ST5.1 Set 5 Result for Player 1 (Numeric-Integer)
FNL.1 Final Number of Games Won by Player 1 (Numeric-Integer)
FSP.2 First Serve Percentage for player 2 (Real Number)
FSW.2 First Serve Won by player 2 (Real Number)
SSP.2 Second Serve Percentage for player 2 (Real Number)
SSW.2 Second Serve Won by player 2 (Real Number)
ACE.2 Aces won by player 2 (Numeric-Integer)
DBF.2 Double Faults committed by player 2 (Numeric-Integer)
WNR.2 Winners earned by player 2 (Numeric)
UFE.2 Unforced Errors committed by player 2 (Numeric)
BPC.2 Break Points Created by player 2 (Numeric)
BPW.2 Break Points Won by player 2 (Numeric)
NPA.2 Net Points Attempted by player 2 (Numeric)
NPW.2 Net Points Won by player 2 (Numeric)
TPW.2 Total Points Won by player 2 (Numeric)
ST1.2 Set 1 result for Player 2 (Numeric-Integer)
ST2.2 Set 2 Result for Player 2 (Numeric-Integer)
ST3.2 Set 3 Result for Player 2 (Numeric-Integer)
ST4.2 Set 4 Result for Player 2 (Numeric-Integer)
ST5.2 Set 5 Result for Player 2 (Numeric-Integer)
FNL.2 Final Number of Games Won by Player 2 (Numeric-Integer)
Round Round of the tournament at which game is played (Numeric-Integer)
いくつか欠測値というかNAがある*1ので、色々迷ったんですがひとまず全部0で置換して埋めてあります。また完全に欠測でNULLになっているところも0で埋めました。なので、厳密には正しくない前処理がかかっている点は悪しからずご了承あれ。
ここでは目的変数としてResult、すなわち勝敗の結果を選びます。つまり全ての変数をPlayer 1の勝利に貢献するかどうかで評価するという形になります。
とりあえずSVMとランダムフォレストで男子の結果に基づいてモデルを推定する
最終的に手元にあるdmとdwは、上記オリジナルデータからFNL.1とFNL.2を削除したものです。理由は簡単で、テニスというスポーツのルール上「勝った方の総ゲーム数は必ず負けた方を上回る」*2ため、勝敗を説明する変数としては不適切だからです。
また、プレイヤー名も男子の中でor女子の中でCVする時には使えるんですが、そもそも参加人数が限られることを考えるとあまり意味がないので、一旦この後の分析では削除します*3。先にResult列をfactor型に直すのも含めて以下のように行います。
dm$Result<-as.factor(dm$Result) dw$Result<-as.factor(dw$Result) dm2<-dm[,3:39] dw2<-dw[,3:39]
その上でチューニングしつつ以下のようにそれぞれSVMとランダムフォレストで分類モデル推定を行います。
> library(e1071) > library(randomForest) > dm2.tune<-tune.svm(Result~.,data=dm2) > dm2.tune$best.model Call: best.svm(x = Result ~ ., data = dm2) Parameters: SVM-Type: C-classification SVM-Kernel: radial cost: 1 gamma: 0.02777778 Number of Support Vectors: 204 > dm2.svm<-svm(Result~.,dm2,cost=1,gamma=dm2.tune$best.model$gamma) > dm2.svm Call: svm(formula = Result ~ ., data = dm2, cost = 1, gamma = dm2.tune$best.model$gamma) Parameters: SVM-Type: C-classification SVM-Kernel: radial cost: 1 gamma: 0.02777778 Number of Support Vectors: 204 > tuneRF(dm2[,-1],dm2[,1],doBest=T) mtry = 6 OOB error = 6.31% Searching left ... mtry = 3 OOB error = 6.52% -0.03225806 0.05 Searching right ... mtry = 12 OOB error = 4.28% 0.3225806 0.05 mtry = 24 OOB error = 5.7% -0.3333333 0.05 Call: randomForest(x = x, y = y, mtry = res[which.min(res[, 2]), 1]) Type of random forest: classification Number of trees: 500 No. of variables tried at each split: 12 OOB estimate of error rate: 3.87% Confusion matrix: 0 1 class.error 0 242 9 0.03585657 1 10 230 0.04166667 > dm2.rf<-randomForest(Result~.,dm2,mtry=12) > dm2.rf Call: randomForest(formula = Result ~ ., data = dm2, mtry = 12) Type of random forest: classification Number of trees: 500 No. of variables tried at each split: 12 OOB estimate of error rate: 3.67% Confusion matrix: 0 1 class.error 0 243 8 0.03187251 1 10 230 0.04166667
randomForestのOOB errorは3.67%と、たかがこの程度のmatch statsでもなかなか正確なんだなーということが分かりますね。ちなみに自己予測をしてみると
> table(dm2$Result,predict(dm2.svm,newdata=dm2[,-1])) 0 1 0 250 1 1 3 237 > table(dm2$Result,predict(dm2.rf,newdata=dm2[,-1])) 0 1 0 251 0 1 0 240
ということで、まぁ悪くないですね。これでSVMとランダムフォレストの分類モデルが出揃いました。
変数重要度を見てみる
自分もテニスプレイヤーである身からすると、気になるのが「どの数字が重要なのか?」ということ。1stサーブが入ってる方が有利?それとも第1セットを大差で奪った方が有利?とか色々思うわけで。。。ということでimportance関数で見てみましょう。
> importance(dm2.rf) MeanDecreaseGini FSP.1 1.326090 FSW.1 3.414751 SSP.1 1.375221 SSW.1 1.774569 ACE.1 2.131037 DBF.1 1.589312 WNR.1 1.532577 UFE.1 1.424780 BPC.1 28.085637 BPW.1 5.113764 NPA.1 1.058818 NPW.1 1.680666 TPW.1 3.227819 ST1.1 9.497543 ST2.1 9.333334 ST3.1 15.241856 ST4.1 9.465749 ST5.1 12.178140 FSP.2 1.550794 FSW.2 3.959450 SSP.2 1.453953 SSW.2 2.711236 ACE.2 1.936136 DBF.2 1.785843 WNR.2 2.226341 UFE.2 1.507302 BPC.2 34.822428 BPW.2 4.745056 NPA.2 1.233000 NPW.2 1.349217 TPW.2 4.884543 ST1.2 9.525584 ST2.2 6.925047 ST3.2 32.095133 ST4.2 9.768185 ST5.2 12.961211 > barplot(c(dm2.rf$importance),names.arg = rownames(dm2.rf$importance),horiz=F,cex.names = 0.7)
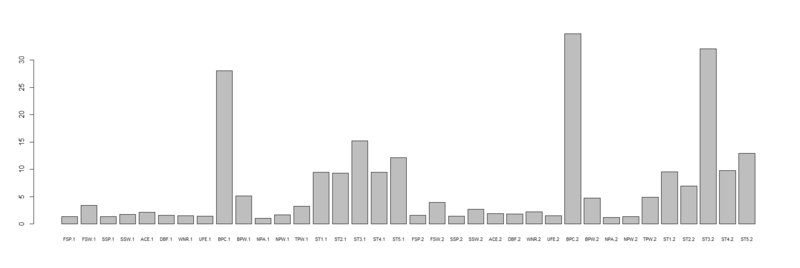
いくつか目立つ変数があるんですが、際立っているのがBPC.1とBPC.2。これ何だっけ?と思ったら、「ブレークポイント創出数(ブレーク機会数)」なんですね。
一般に、ATP(プロテニス男子)ツアーでは誰もが200km超のビッグサーブを打つのが当たり前で、リターンゲーム(相手のサービスゲーム)というのはなかなか取れないもの。なので、いかにしてリターンゲームを取る(ブレークする)かが重要とされます。
で、「ブレークポイント」というのは要はリターンゲームで先に40に達するか、アドバンテージ・レシーバーとなるポイントに達することを指します。レシーバーから見て「このポイントを取ればゲームが取れる」ポイントであり、言ってみれば勝つためのチャンスです。この機会を創り出す多ければ多いほど相手にプレッシャーをかけることができます。
ところが、面白かったのが「実際にブレークに成功した数(BPW.1 / BPW.2)」よりも「ブレーク機会数(BPC.1 / BPC.2)」の方が重要度が高いこと。結果的にブレークに成功したかどうかよりも、相手にそれだけプレッシャーをかけられた方が最終的に勝っている(そして恐らく負けたPlayer 2側でも高いところを見るとBPCが少ないと最終的に負ける)というわけです。これは実は個人的には意外で面白かったです。
男子のモデルで女子の結果を予測してみる
さて、モデルの中身は大体分かったので、予測してみましょう。でも男子内部でやってもその汎化ぶりが分からないので、一見掟破りに見えますが男子のSVM / ランダムフォレストの分類モデルで女子の結果を予測してみます。
> table(dw2$Result,predict(dm2.svm,newdata=dw2[,-1])) 0 1 0 217 10 1 13 212 # 正答率94.9% > table(dw2$Result,predict(dm2.rf,newdata=dw2[,-1])) 0 1 0 222 5 1 5 220 # 正答率97.8%
意外にもかなりの高精度になりました。これまた個人的には結構意外な感があって、「へーーーーーWTAでもそんなにブレーク機会数の方が重要なくらいサービスキープ当たり前の世界が広がってるのか」という感じです。ちなみに女子の方の変数重要度が見てみたいのでrandomForestで推定してみると、
> tuneRF(dw2[,-1],dw2[,1],doBest=T) mtry = 6 OOB error = 1.55% Searching left ... mtry = 3 OOB error = 3.1% -1 0.05 Searching right ... mtry = 12 OOB error = 1.11% 0.2857143 0.05 mtry = 24 OOB error = 1.11% 0 0.05 Call: randomForest(x = x, y = y, mtry = res[which.min(res[, 2]), 1]) Type of random forest: classification Number of trees: 500 No. of variables tried at each split: 12 OOB estimate of error rate: 0.88% Confusion matrix: 0 1 class.error 0 224 3 0.013215859 1 1 224 0.004444444 > dw2.rf<-randomForest(Result~.,dw2,mtry=12) > importance(dw2.rf) MeanDecreaseGini FSP.1 0.6028805 FSW.1 7.3351962 SSP.1 0.5618011 SSW.1 1.6264988 ACE.1 0.6920522 DBF.1 0.5292140 WNR.1 1.7804903 UFE.1 1.9209395 BPC.1 13.7550851 BPW.1 6.0022307 NPA.1 1.1241421 NPW.1 1.0004857 TPW.1 3.0881920 ST1.1 28.3050922 ST2.1 28.2379261 ST3.1 29.8653854 ST4.1 0.0000000 ST5.1 0.0000000 FSP.2 0.6475287 FSW.2 4.0541477 SSP.2 0.6163471 SSW.2 1.2344994 ACE.2 0.7510999 DBF.2 0.6723578 WNR.2 1.1824890 UFE.2 3.7529122 BPC.2 4.4327094 BPW.2 3.8838350 NPA.2 0.7812590 NPW.2 0.7722206 TPW.2 2.0182145 ST1.2 23.5909031 ST2.2 22.0260401 ST3.2 28.6395859 ST4.2 0.0000000 ST5.2 0.0000000 > barplot(c(dw2.rf$importance),names.arg = rownames(dw2.rf$importance),horiz=F,cex.names = 0.7)
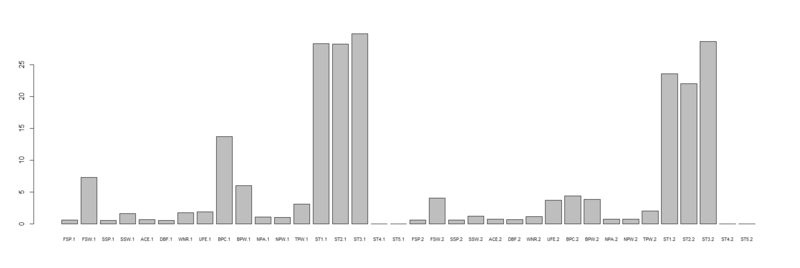
打って変わって各セットでの獲得ゲーム数の影響が大きいですね。。。それだけ大差がついてる試合が多いんですかね? いや、そうだっけ? ってことは。。。
各セットの獲得ゲーム数を削除してもう一度やり直してみる
そう、最初に「総獲得ゲーム数」を削除したのに各セットの獲得ゲーム数を削除してなかったのでしたorz これはこれで重要といえば重要なんですが、結局これも結果と紐付いている変数なので正しくなさそうです。なので、各セットの獲得ゲーム数を削除してもう一度やってみましょう。
> dm3<-dm2 > dm3$ST1.1<-c() > dm3$ST2.1<-c() > dm3$ST3.1<-c() > dm3$ST4.1<-c() > dm3$ST5.1<-c() > dm3$ST1.2<-c() > dm3$ST2.2<-c() > dm3$ST3.2<-c() > dm3$ST4.2<-c() > dm3$ST5.2<-c() > dw3<-dw2 > dw3$ST1.1<-c() > dw3$ST2.1<-c() > dw3$ST3.1<-c() > dw3$ST4.1<-c() > dw3$ST5.1<-c() > dw3$ST1.2<-c() > dw3$ST2.2<-c() > dw3$ST3.2<-c() > dw3$ST4.2<-c() > dw3$ST5.2<-c()
何だこの糞コードとか言わないでorz 後は普通に同じことやるだけです。
> dm3.tune<-tune.svm(Result~.,data=dm3) > dm3.tune$best.model Call: best.svm(x = Result ~ ., data = dm3) Parameters: SVM-Type: C-classification SVM-Kernel: radial cost: 1 gamma: 0.03846154 Number of Support Vectors: 231 > dm3.svm<-svm(Result~.,dm3,cost=1,gamma=dm3.tune$best.model$gamma) > tuneRF(dm3[,-1],dm3[,1],doBest=T) mtry = 5 OOB error = 10.79% Searching left ... mtry = 3 OOB error = 12.63% -0.1698113 0.05 Searching right ... mtry = 10 OOB error = 12.42% -0.1509434 0.05 Call: randomForest(x = x, y = y, mtry = res[which.min(res[, 2]), 1]) Type of random forest: classification Number of trees: 500 No. of variables tried at each split: 5 OOB estimate of error rate: 10.39% Confusion matrix: 0 1 class.error 0 229 22 0.0876494 1 29 211 0.1208333 > dm3.rf<-randomForest(Result~.,dm3,mtry=5) > dm3.rf Call: randomForest(formula = Result ~ ., data = dm3, mtry = 5) Type of random forest: classification Number of trees: 500 No. of variables tried at each split: 5 OOB estimate of error rate: 9.78% Confusion matrix: 0 1 class.error 0 231 20 0.07968127 1 28 212 0.11666667 > table(dw3$Result,predict(dm3.svm,newdata=dw3[,-1])) 0 1 0 210 17 1 17 208 # 正答率92.5% > table(dw3$Result,predict(dm3.rf,newdata=dw3[,-1])) 0 1 0 219 8 1 19 206 # 正答率96.2%
randomForestのOOB errorが9.78%に上がりましたが、男子の分類モデルで女子の結果を予測した結果はそれほど悪くなってません。変数重要度を見てみましょう。
> importance(dm3.rf) MeanDecreaseGini FSP.1 3.393704 FSW.1 6.323733 SSP.1 3.744789 SSW.1 4.877575 ACE.1 6.023498 DBF.1 3.886220 WNR.1 4.767306 UFE.1 3.341895 BPC.1 40.832482 BPW.1 21.418975 NPA.1 3.482657 NPW.1 2.940436 TPW.1 11.135520 FSP.2 3.357201 FSW.2 10.112785 SSP.2 3.433470 SSW.2 5.292208 ACE.2 6.303114 DBF.2 3.771373 WNR.2 6.827519 UFE.2 3.841238 BPC.2 44.329237 BPW.2 20.888179 NPA.2 3.975112 NPW.2 3.533628 TPW.2 13.019895 > barplot(c(dm3.rf$importance),names.arg = rownames(dm3.rf$importance),horiz=F,cex.names = 0.7)
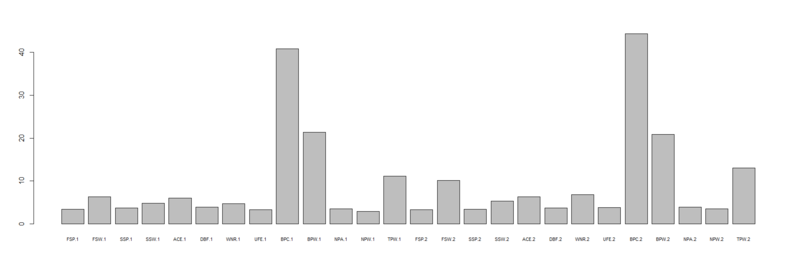
今度はTPW.1/2(総獲得ポイント数)の影響が上がってきたものの、全体としてはBPC.1/2(ブレーク機会数)とBPW.1/2(ブレーク成功数)の影響が大きいという構図に変わりはありません。
その中で目に付くのがFSW.2(Player 2の1stサーブ時獲得ポイント数)の影響度が意外と大きいこと。これはPlayer 1のそれよりも大きいんですね。つまり「1stサーブ時にポイントが取れないほど負けやすい」ことを示しています。あー、これ分かるわ。。。
なお、多分僕同様に長年テニスをやってる人なら不思議に思うかもしれないのがUFE.1/2(アンフォーストエラー数)の変数重要度があまり高くないというかほとんどない点。比較の問題で言えばWNR.1/2(ウィナー数)の方が高いということで、これはエラーしてでもウィナーを多く取った方が勢いがつくってことなのかもしれませんね。
ということで、まとめ
皆さん説明変数の取捨選択には十二分に気をつけましょうorz 実は後半部分はRハンズオンでも触れ損ねたところだったので、今回気付いて良かったです。。。
UCI機械学習リポジトリには他にも面白いデータが山ほど転がっているので、暇を見て色々遊びながら自分の練習にでもしようかなと思ってます。
追記1
やっぱりTPW.1/2(総獲得ポイント数)は使わない方がいいんじゃないかなぁと思い直して、削除したバージョンでもう一度やってみました。
> dm4<-dm3 > dw4<-dw3 > dm4$TPW.1<-c() > dm4$TPW.2<-c() > dw4$TPW.1<-c() > dw4$TPW.2<-c() > dm4.tune<-tune.svm(Result~.,data=dm4) > dm4.tune$best.model Call: best.svm(x = Result ~ ., data = dm4) Parameters: SVM-Type: C-classification SVM-Kernel: radial cost: 1 gamma: 0.04166667 Number of Support Vectors: 225 > dm4.svm<-svm(Result~.,dm4,cost=1,gamma=dm4.tune$best.model$gamma) > tuneRF(dm4[,-1],dm4[,1],doBest=T) mtry = 4 OOB error = 10.59% Searching left ... mtry = 2 OOB error = 14.66% -0.3846154 0.05 Searching right ... mtry = 8 OOB error = 11% -0.03846154 0.05 Call: randomForest(x = x, y = y, mtry = res[which.min(res[, 2]), 1]) Type of random forest: classification Number of trees: 500 No. of variables tried at each split: 4 OOB estimate of error rate: 12.02% Confusion matrix: 0 1 class.error 0 225 26 0.1035857 1 33 207 0.1375000 > dm4.rf<-randomForest(Result~.,dm4,mtry=4) > importance(dm4.rf) MeanDecreaseGini FSP.1 4.478349 FSW.1 7.351250 SSP.1 4.360970 SSW.1 5.423985 ACE.1 7.214073 DBF.1 4.526553 WNR.1 6.557089 UFE.1 4.593019 BPC.1 40.453538 BPW.1 22.406822 NPA.1 4.107380 NPW.1 3.738320 FSP.2 4.269662 FSW.2 11.518477 SSP.2 4.000530 SSW.2 6.670631 ACE.2 7.327702 DBF.2 5.288526 WNR.2 7.633424 UFE.2 5.231134 BPC.2 44.655374 BPW.2 23.135701 NPA.2 5.003801 NPW.2 4.936788 > barplot(c(dm4.rf$importance),names.arg=c(rownames(dm4.rf$importance))) > table(dw4$Result,predict(dm4.svm,newdata=dw4[,-1])) 0 1 0 210 17 1 19 206 # 正答率92% > table(dw4$Result,predict(dm4.rf,newdata=dw4[,-1])) 0 1 0 217 10 1 26 199 # 正答率92% # 実はSVMとランダムフォレストの正答率が全く同じになった
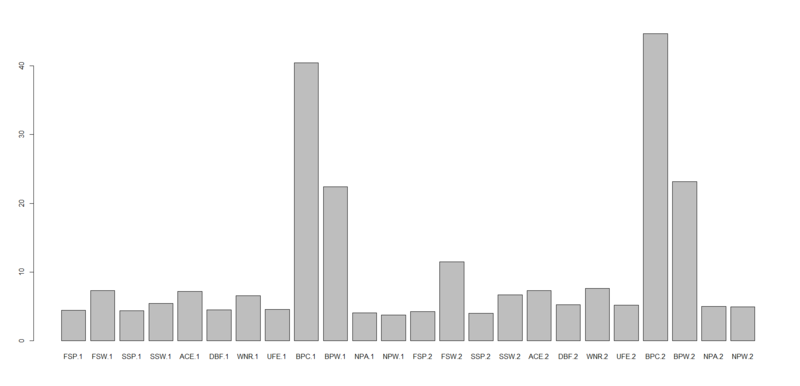
見た感じ、変数重要度にはそれほど大きな差はないようです。けれども、総獲得ポイント数を説明変数から削除した途端にランダムフォレストの精度が下がり、OOB errorは12%にも及び、女子のデータに適用した場合の正答率はSVMと同じになりました。
汎化が強めに出るSVMと、過学習気味になりやすいランダムフォレストとが同じようなパフォーマンスになるというのはちょっと興味深いのですが、これはまた別に検証が必要ということで。。。
追記2
ついでなので、SVM・ランダムフォレストのそれぞれでどの女子の試合の結果予測に失敗したかを調べてみました。
> res<-data.frame(names1=dw$Player1,names2=dw$Player2,actual=dw$Result,predicted1=predict(dm4.svm,newdata=dw4[,-1]),predicted2=predict(dm4.rf,newdata=dw4[,-1])) > res[res$actual!=res$predicted1,] names1 names2 actual predicted1 predicted2 8 Kiki Bertens Ana Ivanovic 0 1 0 37 Sorana Cirstea Marina Erakovic 0 1 0 39 Lesia Tsurenko Varvara Lepchenko 0 1 0 45 Alize Cornet Polona Hercog 0 1 1 58 Tadeja Majeric Ajla Tomljanovic 0 1 0 69 Jie Zheng Madison Keys 1 0 0 72 Lauren Davis Julia Goerges 1 0 0 85 Carla Suarez Navarro Galina Voskoboeva 1 0 0 88 Karin Knapp Maria Sharapova 1 0 0 101 Na Li Lucie Safarova 1 0 0 131 Tamira Paszek Melanie Oudin 0 1 0 140 Jamie Hampton Lucie Safarova 1 0 0 148 Flavia Pennetta Kirsten Flipkens 0 1 0 151 Marion Bartoli Olga Govortsova 1 0 0 204 Ashleigh Barty Maria Kirilenko 0 1 1 210 Shelby Rogers Carla Suarez Navarro 0 1 0 248 Jelena Jankovic Maria Sharapova 0 1 1 264 E.Bouchard G.Voskoboeva 1 0 0 265 S.Arvidsson M.Lucic-Baroni 0 1 0 272 M.Larcher De Brito M.Oudin 1 0 0 304 K.Kanepi T.Moore 1 0 0 327 C.Giorgi S.Cirstea 1 0 0 330 S.Stephens A.Petkovic 1 0 0 344 K.Date-Krumm A.Cadantu 1 0 1 346 A.Cornet F.Pennetta 0 1 1 359 L.Robson M.Erakovic 1 0 0 363 P.Kvitova C.Suarez Navarro 1 0 0 369 S.Williams S.Lisicki 0 1 0 385 S Halep F Pennetta 0 1 0 397 J Glushko D Hantuchova 0 1 1 401 A.Radwanska A Pavlyuchenkova 1 0 1 411 C McHale E Svitolina 1 0 1 421 V Williams J Zheng 0 1 0 424 L Robson C Garcia 1 0 1 430 V Duval S Stosur 1 0 0 443 M Minella S Stephens 0 1 0 > res[res$actual!=res$predicted2,] names1 names2 actual predicted1 predicted2 14 Alison Van Uytvanck Virginie Razzano 0 0 1 21 Ekaterina Makarova Venus Williams 1 1 0 25 Angelique Kerber Jarmila Gajdosova 1 1 0 45 Alize Cornet Polona Hercog 0 1 1 69 Jie Zheng Madison Keys 1 0 0 72 Lauren Davis Julia Goerges 1 0 0 85 Carla Suarez Navarro Galina Voskoboeva 1 0 0 88 Karin Knapp Maria Sharapova 1 0 0 101 Na Li Lucie Safarova 1 0 0 140 Jamie Hampton Lucie Safarova 1 0 0 151 Marion Bartoli Olga Govortsova 1 0 0 154 Stefanie Voegele Heather Watson 1 1 0 167 Nadia Petrova Monica Puig 0 0 1 172 Urszula Radwanska Venus Williams 1 1 0 177 Jana Cepelova Christina McHale 1 1 0 203 Marion Bartoli Mariana Duque-Marino 1 1 0 204 Ashleigh Barty Maria Kirilenko 0 1 1 205 Kaia Kanepi Stefanie Voegele 1 1 0 248 Jelena Jankovic Maria Sharapova 0 1 1 264 E.Bouchard G.Voskoboeva 1 0 0 272 M.Larcher De Brito M.Oudin 1 0 0 273 L.Hradecka K.Knapp 0 0 1 285 S.Soler-Espinosa M.Doi 1 1 0 304 K.Kanepi T.Moore 1 0 0 305 M.Burdette U.Radwanska 0 0 1 323 C.Suarez Navarro M.Lucic-Baroni 1 1 0 327 C.Giorgi S.Cirstea 1 0 0 328 M.Bartoli C.McHale 1 1 0 330 S.Stephens A.Petkovic 1 0 0 346 A.Cornet F.Pennetta 0 1 1 359 L.Robson M.Erakovic 1 0 0 363 P.Kvitova C.Suarez Navarro 1 0 0 372 A.Radwanska N.Li 1 1 0 383 A Ivanovic V Azarenka 0 0 1 397 J Glushko D Hantuchova 0 1 1 430 V Duval S Stosur 1 0 0
何となく傾向がありそうでなさそうな結果なんですが*4、これだけ見ていても仕方ないので誤判定されたサンプルだけを使ってランダムフォレストの分類モデルを推定し、その変数重要度を見てみます。
> idx<-which(res$actual!=res$predicted1|res$actual!=res$predicted2) > idx [1] 8 14 21 25 37 39 45 58 69 72 85 88 101 131 140 148 151 154 167 172 177 203 204 205 210 248 264 265 272 273 285 304 305 [34] 323 327 328 330 344 346 359 363 369 372 383 385 397 401 411 421 424 430 443 > tuneRF(dw4[idx,-1],dw4[idx,1],doBest=T) mtry = 4 OOB error = 34.62% Searching left ... mtry = 2 OOB error = 26.92% 0.2222222 0.05 mtry = 1 OOB error = 44.23% -0.6428571 0.05 Searching right ... mtry = 8 OOB error = 40.38% -0.5 0.05 Call: randomForest(x = x, y = y, mtry = res[which.min(res[, 2]), 1]) Type of random forest: classification Number of trees: 500 No. of variables tried at each split: 2 OOB estimate of error rate: 32.69% Confusion matrix: 0 1 class.error 0 11 11 0.5 1 6 24 0.2 > dw4_false.rf<-randomForest(Result~.,dw4[idx,],mtry=2) > dw4_false.rf Call: randomForest(formula = Result ~ ., data = dw4[idx, ], mtry = 2) Type of random forest: classification Number of trees: 500 No. of variables tried at each split: 2 OOB estimate of error rate: 34.62% Confusion matrix: 0 1 class.error 0 10 12 0.5454545 1 6 24 0.2000000 > importance(dw4_false.rf) MeanDecreaseGini FSP.1 1.0430330 FSW.1 2.3864147 SSP.1 0.9143725 SSW.1 0.8364949 ACE.1 0.6901433 DBF.1 0.9256909 WNR.1 1.1882832 UFE.1 1.1402268 BPC.1 1.0722627 BPW.1 0.9630243 NPA.1 1.0757179 NPW.1 0.9913457 FSP.2 1.0406653 FSW.2 0.9847548 SSP.2 0.9199134 SSW.2 0.8876915 ACE.2 0.7315410 DBF.2 0.6752135 WNR.2 1.3790025 UFE.2 0.9585957 BPC.2 0.9941429 BPW.2 1.1534847 NPA.2 0.9699186 NPW.2 0.9360918 > barplot(c(dw4_false.rf$importance),names.arg=c(rownames(dw4_false.rf$importance)))
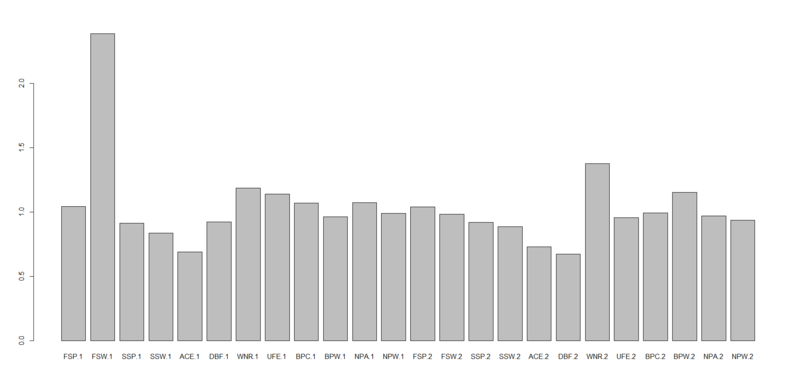
実際にはOOB errorが非常に大きい(33%を超える)ので必ずしも適切な評価とは言えないのですが、この誤判定サンプルから推定し直したモデルの変数重要度を見るとBPC.1/2の重要度が大幅に下がり、代わりにFSW.1が図抜けて大きくなっています。このサンプル群に限っては、とにかくPlayer 1の1stサーブ獲得ポイントがカギだったということのようです。