Rでベイジアン動的線形モデルを学ぶ(5)：説明変数のあるローカル・レベル・モデル

何か月1回しか書かなくなりつつあるこのシリーズですが、中には@berobero11さんのように~~ツッコミ倒すのを~~楽しみにして下さっている方もおられるようなので、久しぶりに更新してみます。

もちろん参考文献は以下の2冊 + PDF book。お題はCommandeur本の第5章「説明変数のあるローカル・レベル・モデル」です。

状態空間時系列分析入門

作者: J.J.F.コマンダー,S.J.クープマン,Jacques J.F. Commandeur,Sime Jan Koopman,和合肇
出版社/メーカー: シーエーピー出版
発売日: 2008/09
メディア: 単行本
購入: 2人クリック: 4回
この商品を含むブログを見る

Rによるベイジアン動的線形モデル (統計ライブラリー)

作者: G.ペトリス,S.ペトローネ,P.カンパニョーリ,和合肇,萩原淳一郎
出版社/メーカー: 朝倉書店
発売日: 2013/05/08
メディア: 単行本
この商品を含むブログ (1件) を見る

An Introduction to State Space Time Series Analysis Summary

ちなみにずっと{dlm}パッケージでやってますが、以前の記事でも紹介したようにもちろんStanなどMCMC系ソフトウェアでモデリング＆パラメータ推定をかけることは可能です。{dlm}パッケージの挙動が気に入らない！という人はStanやBUGSでやるというのも良いかと思います。

説明変数

仰々しく説明変数とか言ってますが、要はこれまで内生変数だけ扱ってきましたがこいつに外生変数を加えて、回帰モデルにしてやろうというお話です。Commandeur本の第5章冒頭49ページには説明変数を加えた観測方程式として

$y_t = \mu_t + \displaystyle \sum^{k}_{j=1} \beta_{jt} x_{jt} + \epsilon_t$ (5.1)

という式になると説明されています。ここで $x_{jt}$ は連続な予測変数で、 $\beta_{jt}$ は $j = 1, \cdots, k$ に対して未知の回帰ウェイト、あるいは回帰係数*1。 $\beta_t = \beta_{1t}$ の1つの予測変数に対して、モデルは $t = 1, \cdots, n$ に対して

$y_t = \mu_t + \beta_t x_t + \epsilon_t, \epsilon_t \sim NID(0, \sigma^2_{\epsilon})$

$\mu_{t+1} = \mu_t + \xi_t, \xi_t \sim NID(0, \sigma^2_{\xi})$

$\beta_{t+1} = \beta_t + \tau_t, \tau_t \sim NID(0, \sigma^2{\tau})$ (5.2)

となります。ちなみに重回帰としてk個の説明変数をモデル化するにはさらにk本の状態方程式が個々の説明変数に対して1セット必要になります。なお上記3本目の撹乱項 $\tau_t$ は回帰関係を安定化させるために0に固定するのが通常だとか。

基本的には上記モデルの3本の式の撹乱項のパラメータ $\sigma^2$ を固定したりフリーにするなりして、最尤法でモデル推定を行う流れになります。

確定的レベルと説明変数

要は $\xi_t$ をゼロに固定するモデルです。ここで(5.2)式のように回帰モデルを立てた場合、Commandeur本pp.50-51でも指摘されているようにごく普通の古典的な線形回帰分析に相当します。

となると、PDF bookにあるように実はこれは{dlm}パッケージを用いるまでもなく、普通にlm関数で線形回帰すればおしまいなのでした。以下そのコード。ただしいつものUK driver KSIをd1として読み込み、対数変換済みtsオブジェクトにしておきます。

# まずUKdriverKSIデータを読み込む
> d1<-read.table("OxCodeIntroStateSpaceBook/Chapter_5/UKdriversKSI.txt",skip=1)
> colnames(d1)<-"logKSI"
> d1<-ts(log(d1),start=c(1969),frequency=12)
# 単純な時間変化で線形回帰したいのでただの1, 2, ...という数列を作る
> t<-1:nrow(d1)
# まずその線形回帰を計算する
> summary(lm(d1~t))

Call:
lm(formula = d1 ~ t)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.33649 -0.10850 -0.01256  0.10368  0.40749 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept)  7.5458427  0.0219747 343.387  < 2e-16 ***
t           -0.0014480  0.0001975  -7.333 6.31e-12 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.1517 on 190 degrees of freedom
Multiple R-squared:  0.2206,	Adjusted R-squared:  0.2165 
F-statistic: 53.77 on 1 and 190 DF,  p-value: 6.313e-12
# 切片＆偏回帰係数ともCommandeur本p.51の通りになった

ところで、Commandeur本p.51と付録AにあるようにこのUK driver KSIデータは石油価格との間に密接な関係があります。これはある意味当たり前で、ガソリン価格が上がればみんなガス代ケチって車に乗らなくなる→交通事故死傷者も減るし、逆なら死傷者は増えるわけです。これも当然ただの線形回帰で関係性を推定することができます。

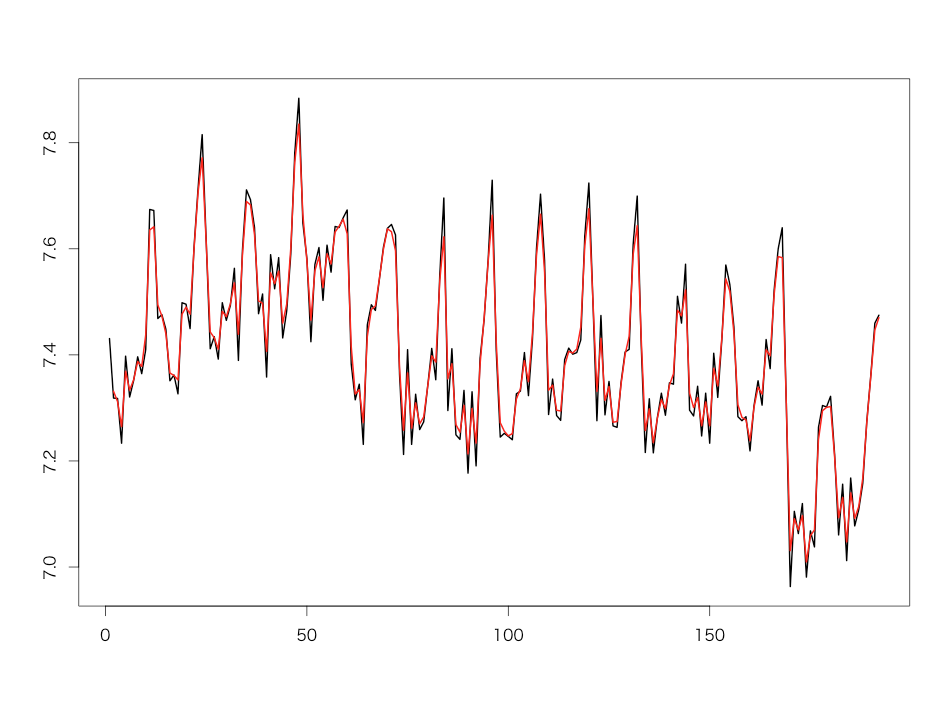
# 石油価格データを読み込む
> x<-read.table("OxCodeIntroStateSpaceBook/Chapter_5/logUKpetrolprice.txt",skip=1)
> x<-ts(x,start=c(1969),frequency=12)

> summary(lm(d1~x))

Call:
lm(formula = d1 ~ x)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.37612 -0.09896 -0.01594  0.09077  0.36594 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  5.87873    0.20889  28.142  < 2e-16 ***
x           -0.67166    0.09173  -7.322 6.74e-12 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.1517 on 190 degrees of freedom
Multiple R-squared:  0.2201,	Adjusted R-squared:  0.216 
F-statistic: 53.61 on 1 and 190 DF,  p-value: 6.742e-12
# 切片＆偏回帰係数ともCommandeur本p.51の通りになった

> matplot(cbind(d1,predict(lm(d1~x),newdata=x)),type='l',lty=1,lwd=2)
# 図5.1をプロットしてみる

f:id:TJO:20150130160036p:plain

これ自体はどちらかというと動的線形モデルとかどうでもいいような、ただの線形回帰です。なので、確定的レベルではなく確率的レベルに問題設定を変更して解き直さないと醍醐味が分からない感があります。

確率的レベルと説明変数

今度は撹乱項をフリーにして、{dlm}パッケージの諸関数を使って最尤推定することを考えます。

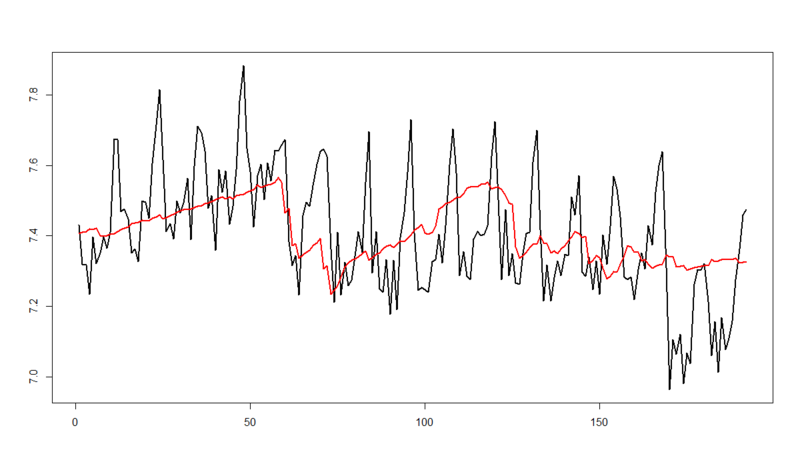
# dlmModeReg関数で単回帰モデルを線形に加える
> build1<-function(params){
+     model<-dlmModPoly(order=1)+dlmModReg(x,addInt = FALSE)
+     V(model)<-exp(params[1])
+     diag(W(model))[1]<-exp(params[2])
+     model
+ }
> fit1<-dlmMLE(d1,rep(0,2),build1) # まず推定
> model1<-build1(fit1$par) # 最尤推定量を突っ込み直してモデル構築
> V(model1)
            [,1]
[1,] 0.002347963
> diag(W(model1))[1]
[1] 0.01166743
# この辺のパラメータはCommandeur本p.55とほぼ一致
> filt1<-dlmFilter(d1,model1) # カルマンフィルタ
> smooth1<-dlmSmooth(filt1) # カルマンスムージング
> smooth1$s[1,1]
[1] 6.82036 # mu1でCommandeur本p.55と一致
> smooth1$s[1,2]
[1] -0.2610497 # beta1でCommandeur本p.55と一致
> matplot(cbind(d1,dropFirst(smooth1$s[,1])),type='l',lty=1,lwd=2)
# じゃあプロットしてみると。。。

f:id:TJO:20150130162531p:plain

あれー。。。PDF bookと全く同じ不一致になってるorz　これ、どう見ても単回帰モデルの側に切片が入ってないからだと思うんですが、ちょっと調べた範囲ではこれを{dlm}パッケージ及びdlmModReg関数の範疇で解決する方法が見つからず。。。うーむ、どうしよう（汗）。

追記（2016年12月27日）

Rでベイジアン動的線形モデルを学ぶ(5)：説明変数のあるローカル・レベル・モデル - 六本木で働くデータサイエンティストのブログ https://t.co/Rpsv3nAk9I
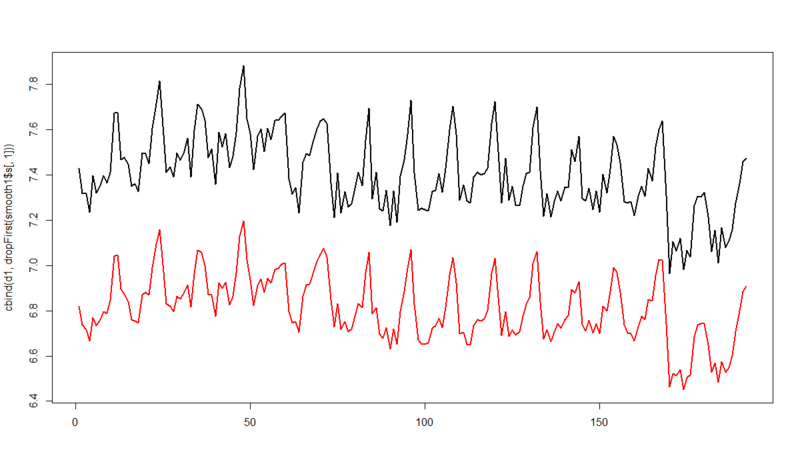
一番下smooth1$s[,1]+smooth$s[,2]*x[,2]て書くのでは。JFF見れないけど pic.twitter.com/XJE089dAy3
— kenji oda(おだちゃニズム) (@kenji_oda0618) 2016年12月27日
という指摘をいただいたので、最後のmatplotのところだけ直しました。
> matplot(cbind(d1,dropFirst(smooth1$s[,1]+smooth1$s[,2]*x)),type='l',lty=1,lwd=2,ylab='')
はい、おかげさまで期待した通りになりました。有難うございます。