渋谷駅前で働くデータサイエンティストのブログ

元祖「六本木で働くデータサイエンティスト」です / 道玄坂→銀座→東京→六本木→渋谷駅前

Rでベイジアン動的線形モデルを学ぶ(2)：まずは状態空間のコンセプトと基本のローカルレベル・モデルから

R 統計学 時系列分析 DLM

前回からだいぶ間が空いた上に、要は{dlm}パッケージで遊ぼう！という大袈裟なタイトルの割に中身のないこのシリーズ記事ですが（笑）、取るものもとりあえずちょっと例題をやってみようと思います。参考文献はまずこちらのPetris本。


Rによるベイジアン動的線形モデル (統計ライブラリー)

Rによるベイジアン動的線形モデル (統計ライブラリー)


あと、以前買ったけどまだ全部読み切ってないこちらのCommandeur*1本も。


状態空間時系列分析入門

状態空間時系列分析入門

  • 作者: J.J.F.コマンダー,S.J.クープマン,Jacques J.F. Commandeur,Sime Jan Koopman,和合肇
  • 出版社/メーカー: シーエーピー出版
  • 発売日: 2008/09
  • メディア: 単行本
  • 購入: 2人 クリック: 4回
  • この商品を含むブログを見る


両者を読んだ印象でいうと、Petris本はRコードが載ってますが説明としてはかなりガチなので僕のような数学苦手マンには割と辛い感じで、一方でCommandeur本は全然Rコードとか何も載ってないものの説明としては豊富な実データを用意した上で実際に数値計算していく過程を細かく説明してくれているので、読むだけなら後者の方が多分楽です。でもRでやるなら前者を外すわけにはいきませんよということで。ということで、この2冊を合わせて読んでいこうと思います。


一応、今回のこのシリーズでは基本的にはサクサク{dlm}パッケージやその関連コードを用いてお手軽に動的線形モデルを回すことを目的としているので、厳密な理論的基礎などについてはできるだけ割愛し、触れても要点だけをまとめる感じでサラッと流す予定です*2。ちなみにCommandeur本では理論的基礎が8章になるまで出てこないので、Petris本と併せて読む場合は先に8章から読み始めた方が良いと思います。


そしてもう一点。実は以前沖本本を読むシリーズをやった際に、基礎を学ぶために参考にさせていただいたLogics of Blueさんのサイトも今回改めて参考にさせていただいてます。その節は大変お世話になり有難うございました。というか、VARまわりについては逆にこちらのブログ記事を参考資料として挙げてくださり、まことに恐縮です。。。


そんなわけで新規性もへったくれもないどころか完全に他人様の褌で相撲を取る状態になってますが（泣）、自分向けの備忘録も兼ねて勉強したものを細々とまとめていこうと思います。


状態空間モデル＝観測方程式＋状態方程式


かつて制御工学を学んだ身には馴染み深い概念なのですが、基本的に状態空間モデルというのはなかなか面白い考え方をしておりまして、「どうせ俺らにはあるシステムの真の状態なんかわかりゃしねーんだよ、見えてるものから当たりをつけて何とかするしかねーんだよ」というイズムのもとで動いてます。


これってプラント制御なんかではままある話らしくて、あれってセンサを設置できない箇所っていうのが色々あって、でもその「センサなし」箇所に由来する不具合やら異常やらって多いんだそうです。そういう時のために例えば「観測器系」というのがあるわけなんですが、多分フィロソフィーとしては同じなんだろうなぁと適当に思ってます。。。Petris本p.41に、樋口本にも載っていたこんな感じの図が出ていますが、


f:id:TJO:20140925231035p:plain


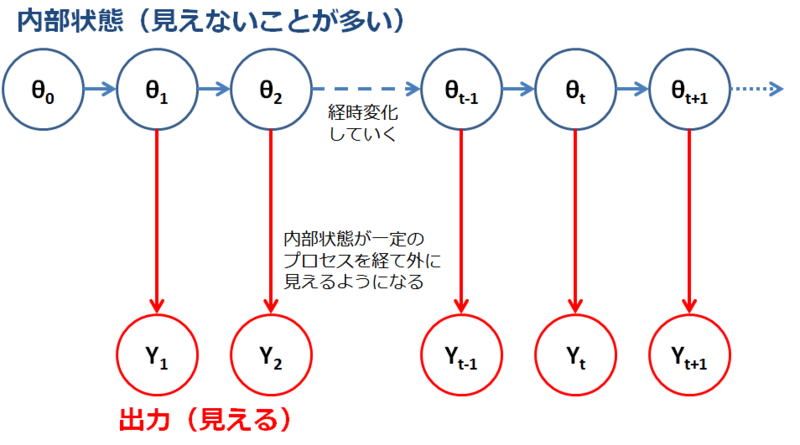
このように「系の出力と、系の実際の内部状態とを分けて考える」のがポイントだというわけです。あくまでも内部の状態だけが経時変化していき、出力はその都度状態を反映するものとして外に見えるだけ。


で、式を並べるんですが、例えばローカル線形トレンドモデルだとこんな感じになります*3。


Y_t = \mu_t + \nu_t, \nu_t \sim \cal{N} (0,V)（観測方程式）

\mu_{t} = \mu_{t-1} + \beta_{t-1} + \omega_{t,1}, \omega_{t,1} \sim \cal{N} (0,\sigma_\mu^2)（状態方程式）

\beta_{t} = \beta_{t-1} + \omega_{t,2}, \omega_{t,2} \sim \cal{N} (0,\sigma_\beta^2)（トレンド方程式）


状態空間モデルのポイントは、計算の手間などもあるのでさくさく行列計算に直してしまうという点*4。上の式は以下のような行列式に帰着できます。


Y_t = F_t \theta_t + \nu_t, \nu_t \sim \cal{N} (0,V_t)（行列化した観測方程式）

\theta_{t+1} = G_t \theta_t + \omega_t, \omega_t \sim \cal{N} (0,W_t)（行列化した状態方程式）

ただし

\theta_t = \begin{bmatrix} \mu_t \\ \beta_t \end{bmatrix}, G = \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix}, W = \begin{bmatrix} \sigma_\mu^2 & 0 \\ 0 & \sigma_\beta^2 \end{bmatrix}, F = \begin{bmatrix} 1 & 0 \end{bmatrix}


制御工学だとここから極配置とかリッカチの方程式を解け*5とか可制御とか可観測*6とかいう方向に行ったりするわけですが、ここでは一旦割愛します*7。必要になったらその都度引き合いに出しますよということで。


ローカルレベル・モデル（ランダムウォーク・プラス・ノイズモデル）


とりあえずどういう時系列を扱うか？ということで以前の沖本本シリーズの記事を思い出してみましょう。最も簡単なのは、基本的にはただのホワイトノイズ（定常過程）なんですが、DLMの世界では何故かランダムウォーク（単位根過程）が一番単純だということになってるんですね。これは実は僕も改めて勉強してびっくりしました。その式を表すと、


Y_t = \mu_t + \nu_t, \nu_t \sim \cal{N} (0,V)（観測方程式）

\mu_t = \mu_{t-1} + \omega_t, \sim \cal{N} (0,W)（状態方程式）


状態方程式が単位根過程を記述してますね。Commandeur本p.10に時刻をt=1,2,3...と変えていった時にどのように時系列データが記述されていくかが説明されています。


厳密な説明は置いといて、とりあえず{dlm}パッケージでやる場合はどうすれば良いかというとdlmModPoly関数でorder=1として定義します。その上でdlmFilter関数でカルマンフィルタによるフィルタ化予測値を得る、というのが一般的な流れです。このカルマンフィルタによるフィルタ化予測値こそが、極めて大ざっぱに言えばDLMを通じて知りたい「（真の）状態値」と言って良いかと思います。


Commandeur本のサンプルデータでやってみる


ざっくりローカルレベル・モデルの話をしたところで、早速適当に例題をやってみたいと思います。Petris本をなぞっても良いのですが、元々Rの本なのにそれを書き写すのはあまりにも芸がないので、違うソースを試してみます。


というのも、実はCommandeur本のサンプルデータが原典の公式サイトに置いてあって、ファイル先頭行のコメントさえ削除すればすぐ使えるようになっています。ということで、試しにChapter 1-2のイギリスの自動車ドライバーの死傷者数データとノルウェーの自動車ドライバーの死傷者数データを使ってみることにしましょう。一方、Petris本の3.2.1節(pp.90-96)に対応する話題が出ているので、やってることはそこからの引き写しです。


イギリスの自動車ドライバーのデータはd1、ノルウェーのデータはd2としてインポートすることにしておきます（やり方は各自でどうぞ）。

> library("dlm")
# ちゃんと{dlm}パッケージを読み込みましょう
> `d1` <- read.table("~/Dev/R/Blog/OxCodeIntroStateSpaceBook/Chapter_1/UKdriversKSI_r.txt", quote="\"")
# インポートは適当に
> d1<-ts(log(d1))
# Commandeur本では対数系列にしているのでlogをとる
> head(d1)
[1] 7.430707 7.318540 7.317876 7.233455 7.397562 7.320527
# 一応確認
> d1.model1<-dlmModPoly(order=1)
# dlmModPoly関数で、ローカルレベル・モデルなのでorder=1でモデリング。
# 残りのパラメータはデフォルトのまま
> d1.filt1<-dlmFilter(d1,d1.model1)
# カルマンフィルタにかける
> matplot(cbind(d1,d1.filt1$m[-1]),type='l',lwd=c(2,3),col=c('red','blue'))
# プロット
> d1.diff<-d1-d1.filt1$m[-1]
> plot(d1.diff,type='l')
> hist(d1.diff,breaks=20)
# Commandeur本の通りフィルタ化系列と実系列との残差をとり、プロットとヒストグラムを描く
> shapiro.test(d1.diff)

	Shapiro-Wilk normality test

data:  d1.diff
W = 0.9781, p-value = 0.004247

# Shapiro-Wilkの正規性検定。Commandeur本でも示唆されているようにダメです

> Box.test(d1.diff)

	Box-Pierce test

data:  d1.diff
X-squared = 10.0395, df = 1, p-value = 0.001532

# Ljung-Boxの独立性検定。これまたダメです

f:id:TJO:20140926143902p:plain

f:id:TJO:20140926143915p:plain

f:id:TJO:20140926143924p:plain


カルマンフィルタで処理した出力のうち、$mにフィルタ化系列が収納されています。で、これを見てみると、Commandeur本pp.16-18でもコメントのあるように、残差が正規性も独立性も満たしていないのでこのローカルレベル・モデルでは当てはまりに問題があるようです。そこで、もう一つのノルウェーのデータでやってみましょう。

> `d2` <- read.delim("~/Dev/R/Blog/OxCodeIntroStateSpaceBook/Chapter_2/NorwayFinland_r.txt", header=FALSE)
>   View(`d2`)
> d2<-log(d2[,2])
> d2.model1<-dlmModPoly(order=1)
> d2.filt1<-dlmFilter(d2,d2.model1)
> matplot(cbind(d2,d2.filt1$m[-1]),type='l',lwd=c(2,3),col=c('red','blue'))
> d2.diff<-d2-d2.filt1$m[-1]
> plot(d2.diff,type='l')
> hist(d2.diff)
> shapiro.test(d2.diff)

	Shapiro-Wilk normality test

data:  d2.diff
W = 0.9763, p-value = 0.6539

# 正規性はOK

> Box.test(d2.diff)

	Box-Pierce test

data:  d2.diff
X-squared = 0.1756, df = 1, p-value = 0.6752

# 独立性もOK

f:id:TJO:20140926144208p:plain

f:id:TJO:20140926144221p:plain

f:id:TJO:20140926144228p:plain


今度はローカルレベル・モデルというか、ランダムウォーク・プラス・ノイズモデルでよく当てはまったようです。これもCommandeur本でコメントされている通り。そこで、ノルウェーのデータのローカルレベル・モデルの一期先予測値と実測値とを比べてみましょう。一期先予測値は$fに収納されています。

> matplot(cbind(d2[-1],d2.filt1$f[-1]),type='l',lwd=c(2,3),col=c('red','purple'))

f:id:TJO:20140926145532p:plain


まぁ何となくうまくいっているように見えますが、これはまた別に評価した方がいいかもですね。。。ということで今回はひとまずここまで。以後おいおいこんなペースでダラダラと例題をやっていきます。

*1:CAP出版さーん、カバーの著者名間違ってますよ。。。

*2:ってか前に沖本本やった時に全部取り上げていたら死にかけたのでorz

*3:正規分布はPetris本だとN、Commandeur本だとNIDと記法が違うんですが、引用する際にいちいち考えるのが面倒なので出典に応じて混在させちゃいますごめんなさい

*4:これで何故データ分析を学ぶのに線形代数が必須だと色々なところで言われるかがお分かりになるのではないかと

*5:Petris本p.81にも出てきます

*6:この辺はPetris本でもバッチリ出てくる

*7:ってか教わった当時も辛うじて試験で単位もらえる程度にしか理解できなかったのでorz