非劣性検定（等価検定）をRで試してみる - 渋谷駅前で働くデータサイエンティストのブログ

この記事は、以前『統計学のセンス』を読んだ時から気になっていたことを思い出したので、単にRで試してみたという備忘録です。

非劣性検定（等価検定）の話題は、本書の最後にある8.3節「非劣性の検証とは？」であくまでも付録扱いとして登場します。ここでは、

統計学的検定は通常「有意差検定」といわれるが、
1) 標本数を大きくすることによって「医学的に有意でない差」を「統計学的に有意」とすることができる
2) 標本数を小さくすることによって「医学的に有意な差」を「統計学的に有意でない」とすることができる
という欠点があることは意外と知られていない。（同書p.143）

という有意差検定の問題点を指摘した上で、1980年代後半ごろから新薬審査に当たって「標準薬と同等程度の有効性」が検証できれば認可されるという流れが出てきたことで、積極的に同等性を検証するというニーズが出てきたという話題が紹介されています。

で、重要なのは「有意差検定で有意でなければ同等」とは言えない、という点です。というのは、皆さんご存知のように通常の有意差検定では帰無仮説 $H_0$ 「差があるとは言えない」を棄却しに行くため、これが棄却できない場合の結論はあくまでも「差があるとは言えない」という玉虫色の状態にしかならないためです。

そこで、通常の有意性検定即ちsuperiority test（優性検定）とは異なるinferiority test（非劣性検定）を別に立てて、これを実践しなければならないというのが本書の指摘です。本書p.144には以下のように解説されています。

非劣性検定の手順

1) $\Delta$ の設定
臨床的にこれ以上劣っては、たとえ他のメリットがあっても標準薬に代わって使用できない差 $\Delta$ を事前に慎重に設定する。言い換えれば、 $\Delta$ 以内は同等と見なせる差である。

2) 検定
次の仮説を統計学的に片側有意水準 $\alpha / 2$ で検定する。
帰無仮説 $H_0$ ： $\Delta$ 以上劣っている
対立仮説 $H_1$ ： $\Delta$ 以上は劣らない
2値データ（比率）の場合、独立な2群の比較にYamagawa-Tango-Hiejimaの検定が、対応のある2群比較にTangoの非劣性検定が適用できる。

3) 統計的に有意な結果が出た（対立仮説が採択された）場合に、有意水準 $\alpha$ で同等である（ $\Delta$ 以上は劣らない）ことが検証されたと解釈する（検定自体は両側有意水準 $\alpha$ である）。

4) 差の信頼区間も表示する。実は、2)の対立仮説は「信頼区間の下限値 > $-\Delta$ 」と対応している。

丹後先生の我田引水が見えなくもないですが（笑）、これは様々な他の文献と相互参照しても同じ内容になっていて*1、尚且つ分かりやすいです。ちなみに模式図にしたものがPubMed Central収録の総説にあって、こちらも分かりやすいです。余談ですが、非劣性検定関連の用語をググるとsuggestに"inferiority margin"（非劣性マージン）という語が出てくるのですが、 $\Delta$ が意味しているのはまさにそれなのでしょう。

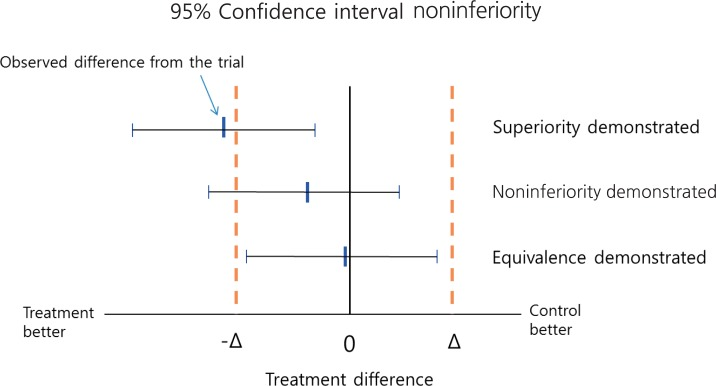
f:id:TJO:20210614170712p:plain

これを見ると、優性検定（有意差検定）・非劣性検定・等価検定はそれぞれ判定のやり方も、そして解釈の仕方も異なるのだということが良く分かります。今回は『統計学のセンス』に倣って非劣性検定にフォーカスを当てているつもりですが、もしかしたら以下に紹介する実践の中身も実は等価検定が混じっているかもしれないのでその点は予めご容赦ください。

そんなわけで非劣性検定を実際にRでやってみようと思い、調べたところ以下の2つのCRANパッケージが見つかりました。

このうち、{equivUMP}はシンプルにequiv.testという関数のみの構成で分かりやすいのですが*2、{EQUIVNONINF}の方は検定力算出などの関数が沢山並んでいていまいち使い方が分からず……どちらもvignettesがないので、諦めて前者のみで試してみることにしました。というか、どなたか後者の詳細に明るい方いらっしゃいましたら是非ご教示くださいm(_ _)m

ちなみにequivUMP::equiv.testもハイパーパラメータがあるので、その設定によっては微妙に結果が変わることが推測されます。Vignettesがないので素のdocを見ると、

対応のない2群の検定においては

$\theta = \displaystyle \frac{\mu_x - \mu_y - \mu}{\sigma}$
（ただし $\sigma$ は2群の標準偏差を統合したものと言っているので、Cohen's dでも用いられる $s = \displaystyle \sqrt{\frac{(n_x-1)s_x^2 + (n_y-1)s_y^2}{n_x+n_x-2}}$ と同じようなものと思われる）

を検定統計量として、

$H_0$ : $\theta \leq -\epsilon$ or $\epsilon \geq \theta$
$H_1$ : $-\epsilon < \theta < \epsilon$

を検定する

と言っているので、 $\epsilon$ 即ちepsが『統計学のセンス』で言うところの非劣性マージン $\Delta$ と似た役割を果たすハイパーパラメータであることが分かります。なおdocを見ると規定値でeps = 1となっています。

では、実際にRでやってみましょう。まず適当に差の無さそうな2群の連続値サンプルを乱数から生成します（再現性のためシードは適当な決め打ちです）。ついでなので、最近覚えた{ggplot2}で適当に図示してみます。

library(ggplot2)
library(equivUMP)

num <- 30

set.seed(51)
x <- rnorm(num, 0, 1)
set.seed(52)
y <- rnorm(num, 0, 1)

d <- rbind(data.frame(name = "A", val = x),
           data.frame(name = "B", val = y))
p <- ggplot(data = d, mapping = aes(x = name, y = val))
p + geom_boxplot(mapping = aes(fill = name)) +
  theme(axis.text.x = element_text(size = 24),
        axis.text.y = element_blank(), legend.position = "none") +
  labs(x = NULL, y = NULL)

f:id:TJO:20210608004724p:plain

あとは、equivUMP::equiv.testで等価検定（あれ？非劣性検定ではない？）をやるだけです。ついでにt検定もやってみます。

equiv.test(val ~ name, d)
#R> 
#R> 	Two sample equivalence test
#R> 
#R> data:  val by name
#R> t = -0.45436, df = 58.000, ncp = 3.873, p-value = 0.0003082
#R> alternative hypothesis: equivalence
#R> null values:
#R>      lower upper
#R> [1,]  -Inf    -1
#R> [2,]     1   Inf
#R> sample estimates:
#R>         d 
#R> -0.117316 
#R> 
t.test(val ~ name, d)
#R> 
#R> 	Welch Two Sample t-test
#R> 
#R> data:  val by name
#R> t = -0.45436, df = 57.712, p-value = 0.6513
#R> alternative hypothesis: true difference in means is not equal to 0
#R> 95 percent confidence interval:
#R>  -0.6355746  0.4004386
#R> sample estimates:
#R> mean in group A mean in group B 
#R>    -0.119963232    -0.002395238 
#R>

等価検定ではp < 0.05即ち「等しい」という結果になり、同時にt検定ではp > 0.05即ち「差があるとは言えない」という結果になりました。これは事前に想定した通りの帰結です。きちんと用意した2群のサンプルが等価であることが示されました。

では、以下のように「少し」ずらしたらどうなるでしょうか？

set.seed(51)
x <- rnorm(num, 0, 1)
set.seed(52)
y <- rnorm(num, 0.45, 1)

d <- rbind(data.frame(name = "A", val = x),
           data.frame(name = "B", val = y))

equiv.test(val ~ name, d)
#R>
#R>	Two sample equivalence test
#R>
#R>data:  val by name
#R>t = -2.1935, df = 58.000, ncp = 3.873, p-value = 0.04897
#R>alternative hypothesis: equivalence
#R>null values:
#R>     lower upper
#R>[1,]  -Inf    -1
#R>[2,]     1   Inf
#R>sample estimates:
#R>         d 
#R>-0.5663513 
#R>
t.test(val ~ name, d)
#R>
#R>	Welch Two Sample t-test
#R>
#R>data:  val by name
#R>t = -2.1935, df = 57.712, p-value = 0.03232
#R>alternative hypothesis: true difference in means is not equal to 0
#R>95 percent confidence interval:
#R> -1.08557457 -0.04956142
#R>sample estimates:
#R>mean in group A mean in group B 
#R>     -0.1199632       0.4476048

もちろんこれは僕がちょっとだけ試行錯誤して作った結果なのですが、等価検定がp < 0.05で「等価である」となると同時にt検定もp < 0.05で「差がある」となっています。これは明らかな矛盾です。そこで同じ「少しだけずらした」2群のサンプルに対して、あえてequivUMP::equiv.testのepsを以下のようにいじってみます。

equiv.test(val ~ name, d, eps = 0.5)
#R>
#R>	Two sample equivalence test
#R>
#R>data:  val by name
#R>t = -2.1935, df = 58.0000, ncp = 1.9365, p-value = 0.5958
#R>alternative hypothesis: equivalence
#R>null values:
#R>     lower upper
#R>[1,]  -Inf  -0.5
#R>[2,]   0.5   Inf
#R>sample estimates:
#R>         d 
#R>-0.5663513

期待通り、等価検定が「等価ではない」になったので矛盾が解消されました。では、以下のような2群のサンプルとepsの設定にしたらどうなるでしょうか？

set.seed(51)
x <- rnorm(num, 0, 1)
set.seed(52)
y <- rnorm(num, 0.1, 1)

d <- rbind(data.frame(name = "A", val = x),
           data.frame(name = "B", val = y))

equiv.test(val ~ name, d, eps = 0.5)
#R>
#R>	Two sample equivalence test
#R>
#R>data:  val by name
#R>t = -0.84083, df = 58.0000, ncp = 1.9365, p-value = 0.1337
#R>alternative hypothesis: equivalence
#R>null values:
#R>     lower upper
#R>[1,]  -Inf  -0.5
#R>[2,]   0.5   Inf
#R>sample estimates:
#R>         d 
#R>-0.2171016 
#R>
t.test(val ~ name, d)
#R>
#R>	Welch Two Sample t-test
#R>
#R>data:  val by name
#R>t = -0.84083, df = 57.712, p-value = 0.4039
#R>alternative hypothesis: true difference in means is not equal to 0
#R>95 percent confidence interval:
#R> -0.7355746  0.3004386
#R>sample estimates:
#R>mean in group A mean in group B 
#R>    -0.11996323      0.09760476

等価検定もt検定も有意ではないので「等価とは言えない」のに「差があるとは言えない」という、どっちつかずの宙ぶらりんの結果になってしまいました……これは難しいものがありますね。

疫学分野に詳しい知人曰くは「結局非劣性マージン $\Delta$ の設定次第で結果がいかようにも変わってしまうので、そもそも非劣性検定（等価検定）は取り扱いが難しい」だそうで、これはまさに『統計学のセンス』が「 $\Delta$ を事前に慎重に設定せよ」と警告していたのと同じ話だと思いました。

ということで、元々統計学を学ぶ過程で色々な本や人が「差が『ない』ことを示すのは難しい」と事あるごとに語っているのを何度も見てきましたが、実際に非劣性検定（等価検定）を触ってみたらそれが良く分かった……という体験談でした。ただし僕もまだまだこの枠組みを理解できたとは思えないので、詳しい方は是非ご教示くださると幸いです。

*1:例えば米FDAのドキュメントなど

*2:パッケージの説明には「stats::t.testと中身は同じで出力が違うだけ」的なことが書かれている