Kaggleはすっかりただの野次馬の一人になって久しいんですが、しばらく前に行われたPetFinder.my - Pawpularity Contestというコンペで優勝者がSVR(サポートベクター回帰)を使ったことが話題になっていたというのを聞いて、NN全盛のこのご時世に意外だなと思ったのでした。
しかし、よくよく考えてみればかのVapnik御大がかつてSVMを考案する際にベースとしたアイデアはNNとは方向性の違う代物だったわけです。故に、例えばSVMとNNとがどのような点で異なるかが「見える化」出来れば、SVMが復権するための条件のようなものが見えてきそうです。
ということで、久しぶりに「サンプルデータで試す機械学習シリーズ」をやってみようと思います。実はDNNについては6年前にも似たようなことをやっているのですが、SVMとDNNとでサンプルサイズを変えながら比較するというのはやったことがないので、今回が初めての試みです。ちなみにGBDT*1も本来は合わせて比較した方が良いのかもしれませんが、単純に面倒なので割愛しました。もしかしたら後日追記で入れるかもしれません。
データセット
かなり以前からGitHubに転がしてある"xor_complex_large.txt", "xor_complex_medium.txt", "xor_complex_small.txt"というデータセットを使います。いわゆるXORパターンでサンプルサイズを10万、1万、100と変えたものです*2。なので、真の決定境界は基本的には「x軸とy軸」です。よって、この十字形の真の決定境界にいかに近いかどうかで分類器の汎化性能がある程度推し測れると期待されます。
SVMでやってみる
e1071::svmを使ってXORパターンの決定境界を描いてみました。いつも通りクソコードなのは伏してご容赦ください。
######### ## SVM ## ######### t <- proc.time() # Large dataset d <- read.csv('https://github.com/ozt-ca/tjo.hatenablog.samples/raw/master/r_samples/public_lib/jp/xor_complex_large.txt', header = T, sep = '\t') d[, 3] <- d[, 3] - 1 d[, 3] <- as.factor(d[, 3]) library(e1071) fit <- svm(label ~., data = d) px <- seq(-4, 4, 0.03) py <- seq(-4, 4, 0.03) d_test <- expand.grid(px, py) names(d_test) <- names(d)[-3] pred_class <- predict(fit, newdata = d_test) plot(d[, -3], col = c(rep(1, 50000), rep(2, 50000)), pch = 19, cex = 0.2, xlim = c(-4, 4), ylim = c(-4, 4), main = "SVM: Large dataset") par(new = T) contour(px, py, array(pred_class, dim = c(length(px), length(py))), xlim = c(-4, 4), ylim = c(-4, 4), levels = 0.5, drawlabels = F, col = 'purple', lwd = 5) # Medium dataset d <- read.csv('https://github.com/ozt-ca/tjo.hatenablog.samples/raw/master/r_samples/public_lib/jp/xor_complex_medium.txt', header = T, sep = '\t') d[, 3] <- d[, 3] - 1 d[, 3] <- as.factor(d[, 3]) library(e1071) fit <- svm(label ~., data = d) px <- seq(-4, 4, 0.03) py <- seq(-4, 4, 0.03) d_test <- expand.grid(px, py) names(d_test) <- names(d)[-3] pred_class <- predict(fit, newdata = d_test) plot(d[, -3], col = c(rep(1, 5000), rep(2, 5000)), pch = 19, cex = 0.4, xlim = c(-4, 4), ylim = c(-4, 4), main = "SVM: Medium dataset") par(new = T) contour(px, py, array(pred_class, dim = c(length(px), length(py))), xlim = c(-4, 4), ylim = c(-4, 4), levels = 0.5, drawlabels = F, col = 'purple', lwd = 5) # Small dataset d <- read.csv('https://github.com/ozt-ca/tjo.hatenablog.samples/raw/master/r_samples/public_lib/jp/xor_complex_small.txt', header = T, sep = ' ') d[, 3] <- d[, 3] - 1 d[, 3] <- as.factor(d[, 3]) library(e1071) fit <- svm(label ~., data = d) px <- seq(-4, 4, 0.03) py <- seq(-4, 4, 0.03) d_test <- expand.grid(px, py) names(d_test) <- names(d)[-3] pred_class <- predict(fit, newdata = d_test) plot(d[, -3], col = c(rep(1, 50), rep(2, 50)), pch = 19, cex = 2, xlim = c(-4, 4), ylim = c(-4, 4), main = "SVM: Small dataset") par(new = T) contour(px, py, array(pred_class, dim = c(length(px), length(py))), xlim = c(-4, 4), ylim = c(-4, 4), levels = 0.5, drawlabels = F, col = 'purple', lwd = 5) (svm_t <- proc.time() - t)
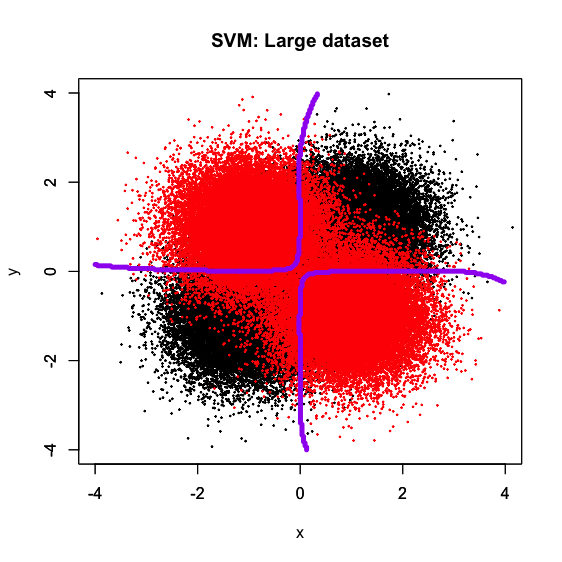


サンプルサイズが減るにつれて決定境界が「粗く」なっていく感じはありますが、小さいサンプルサイズで疎らであっても一応十字型の真の決定境界に何となく合わせてきている様子が見て取れるかと思います。ちなみにRコードを見ての通り、パラメータチューニングは一切かけず、LIBSVM系統のデフォルトパラメータで回しています。
R版KerasのDNNでやってみる
SVMの結果だけ見てもそのご利益は分からないので、比較としてDNNで決定境界を描いてみます。これは以前の記事でも組んだR版Kerasによるもので、サンプルサイズlargeの時に綺麗な十字型の決定境界を描くようにパラメータを設定してあります。なお、NN系の常としてrandom seedが変わることで多少結果が異なる点にご留意ください。
######### ## DNN ## ######### t <- proc.time() # Large dataset d <- read.csv('https://github.com/ozt-ca/tjo.hatenablog.samples/raw/master/r_samples/public_lib/jp/xor_complex_large.txt', header = T, sep = '\t') x_train <- as.matrix(d[, -3]) y_train <- as.matrix(d[, 3]) - 1 library(keras) model <- keras_model_sequential() model %>% layer_dense(units = 5, input_shape = 2) %>% layer_activation(activation = 'relu') %>% layer_dense(units = 7) %>% layer_activation(activation = 'relu') %>% layer_dense(units = 1, activation = 'sigmoid') model %>% compile( loss = 'binary_crossentropy', optimizer = optimizer_sgd(lr = 0.05), metrics = c('accuracy') ) model %>% fit(x_train, y_train, epochs = 5, batch_size = 100) px <- seq(-4, 4, 0.03) py <- seq(-4, 4, 0.03) x_test <- expand.grid(px, py) x_test <- as.matrix(x_test) pred_class <- model %>% predict(x_test, batch_size = 100) pred_class <- round(pred_class, 0) plot(d[, -3], col = c(rep(1, 50000), rep(2, 50000)), pch = 19, cex = 0.2, xlim = c(-4, 4), ylim = c(-4, 4), main = "DNN: Large dataset") par(new = T) contour(px, py, array(pred_class, dim = c(length(px), length(py))), xlim = c(-4, 4), ylim = c(-4, 4), levels = 0.5, drawlabels = F, col = 'purple', lwd = 5) # Medium dataset d <- read.csv('https://github.com/ozt-ca/tjo.hatenablog.samples/raw/master/r_samples/public_lib/jp/xor_complex_medium.txt', header = T, sep = '\t') x_train <- as.matrix(d[, -3]) y_train <- as.matrix(d[, 3]) - 1 library(keras) model <- keras_model_sequential() model %>% layer_dense(units = 5, input_shape = 2) %>% layer_activation(activation = 'relu') %>% layer_dense(units = 7) %>% layer_activation(activation = 'relu') %>% layer_dense(units = 1, activation = 'sigmoid') model %>% compile( loss = 'binary_crossentropy', optimizer = optimizer_sgd(lr = 0.05), metrics = c('accuracy') ) model %>% fit(x_train, y_train, epochs = 5, batch_size = 100) px <- seq(-4, 4, 0.03) py <- seq(-4, 4, 0.03) x_test <- expand.grid(px, py) x_test <- as.matrix(x_test) pred_class <- model %>% predict(x_test, batch_size = 100) pred_class <- round(pred_class, 0) plot(d[, -3], col = c(rep(1, 5000), rep(2, 5000)), pch = 19, cex = 0.4, xlim = c(-4, 4), ylim = c(-4, 4), main = "DNN: Medium dataset") par(new = T) contour(px, py, array(pred_class, dim = c(length(px), length(py))), xlim = c(-4, 4), ylim = c(-4, 4), levels = 0.5, drawlabels = F, col = 'purple', lwd = 5) # Small dataset d <- read.csv('https://github.com/ozt-ca/tjo.hatenablog.samples/raw/master/r_samples/public_lib/jp/xor_complex_small.txt', header = T, sep = ' ') x_train <- as.matrix(d[, -3]) y_train <- as.matrix(d[, 3]) - 1 library(keras) model <- keras_model_sequential() model %>% layer_dense(units = 5, input_shape = 2) %>% layer_activation(activation = 'relu') %>% layer_dense(units = 7) %>% layer_activation(activation = 'relu') %>% layer_dense(units = 1, activation = 'sigmoid') model %>% compile( loss = 'binary_crossentropy', optimizer = optimizer_sgd(lr = 0.05), metrics = c('accuracy') ) model %>% fit(x_train, y_train, epochs = 5, batch_size = 100) px <- seq(-4, 4, 0.03) py <- seq(-4, 4, 0.03) x_test <- expand.grid(px, py) x_test <- as.matrix(x_test) pred_class <- model %>% predict(x_test, batch_size = 100) pred_class <- round(pred_class, 0) plot(d[, -3], col = c(rep(1, 50), rep(2, 50)), pch = 19, cex = 2, xlim = c(-4, 4), ylim = c(-4, 4), main = "DNN: Small dataset") par(new = T) contour(px, py, array(pred_class, dim = c(length(px), length(py))), xlim = c(-4, 4), ylim = c(-4, 4), levels = 0.5, drawlabels = F, col = 'purple', lwd = 5) (dnn_t <- proc.time() - t)



DNNだとサンプルサイズlargeでは綺麗な十字型の決定境界を描くものの、mediumになった時点で程度問題ながら歪み始め、smallでは見る影もないという結果になっています。何度か繰り返して自動でrandom seedを変えることで決定境界の形に多少バリエーションが出ますが、それでも「パラメータを固定するとlargeの時だけ典型的な十字型の決定境界を描くが、mediumで歪み始め、smallでは殆ど上手くいかない」というシチュエーションは一貫して変わらないようです。

ただ、ミニバッチサイズを固定するのは流石にNNに対しては不公平だと思ったので、smallの時だけミニバッチサイズを5にしてやり直した結果がこちらです。一応、十字型の決定境界に沿うような感じになっていますが、「デフォルトではこうはならない(というかデフォルトがない)」という点に留意が必要かと。
考察
今回の限られたデータセットに対する実験だけで確定的な結論など出せるはずもないのですが、それでも「SVMはデフォルトパラメータで小さなサンプルサイズであってもそこそこ高いパフォーマンスを出せる」ということは言えるかもしれません。それはやはりマージン最大化とサポートベクター選択によるスパース化というアルゴリズム自身が持つ強みなのでしょう。確か冒頭に挙げたPetFinderコンペもサンプルサイズは結構小さかったはずで、ある意味SVM (SVR)が活躍できる素地が揃っていたとも言えそうです。
現代では「特に理由がなければ初手NN(もしくはGBDT)」というのが常態化しているように見受けられますが、SVMはデフォルトパラメータが存在している上にそれでもそこそこの性能が出るので、その点は「お手軽」だと個人的には見ています*3。そういう意味での、SVMの復権の余地もあるのかも?という気はします。
ただ、僕も以前から何度か指摘していますが、現代の機械学習におけるSVMの難点は「分散処理ができず計算負荷も時間もかかる」点でしょう。
svm_t #R> ユーザ システム 経過 #R> 222.141 2.267 240.272 dnn_t #R> ユーザ システム 経過 #R> 16.470 1.334 21.129
実際に計算時間を比べてみるとご覧の通りで、何と10倍近くも違います。これはやはりDNNだと学習も予測もミニバッチで分散可能なのに対して、SVMだと全て逐次処理で分散できないことが影響しているのでしょう。たかが2次元で最大10万行のデータセットでこのザマなので、実運用になると途方もない差になるのではないかと思われます。一方で、上記のように「SVMは小サンプルサイズの方が有利」となれば、むしろその場合はNNとの差がつきにくいので、尚更SVMで回すことによるメリットが出てくるかもしれません。
今回のRコードもGitHubに上げてありますので、追試などして下さる方がいらっしゃれば大歓迎です。その際は是非コメントなどで結果をお知らせいただけると幸いです。
余談:R版Kerasの再インストール
実は、この記事を書くに当たって幾星霜ぶりかでR版Kerasを立ち上げたんですが、立ち上げた瞬間にKerasが勝手にPython環境をアップデートしてしまったことで却ってversion conflictが起きてしまい、以後何度Kerasを走らせようとしても毎回Rセッションがクラッシュしてしまうという状況になってしまったのでした。
で、だいぶ色々ググりまくって、最終的にたどり着いたのがこちらの解決策でした。
install.packages("remotes") remotes::install_github(sprintf("rstudio/%s", c("reticulate", "tensorflow", "keras"))) reticulate::miniconda_uninstall() # start with a blank slate reticulate::install_miniconda() keras::install_keras()
要はR版Kerasは勝手にminicondaを入れてしまうので、一度minicondaをまっさらにしてから入れ直すと上手くいくということのようです。僕の場合もこれで無事にR版Kerasが回るようになりました。