MXnet / Kerasが本格的に普及してきたことで、いよいよ「誰でも(割と)気軽にDeep Learningを実践できる」時代になってきましたね、という話を前回の記事では一通りやってみました。
ということで、これからしばらく「気軽に実践できるようになったけど実際問題Deep Learningってどうなん?」というのを色々サンプルデータセットを替えて学習&予測の挙動を見ることで、その実態を体感してみようという技術ネタシリーズをダラダラやってみようかと思います。
フレームワークはMXnet / Kerasどちらでも良いつもりですが、単に自分の環境でのお手軽さを優先して基本的にMXnetで統一しようと思います。リクエストがあればKerasでの実行例も後から追記するようにしますので、どうしてもKerasでどう回すか分からない!という方はコメント欄なりでご一報ください。
追記部分について
非常に重要なポイントが追記部分に含まれている&追記部分に書かれている方が正しいR実行例なので、必ずそちらもご参照ください
Tennis: テニス四大大会データセット
TennisはUCI ML Repositoryの定番データセットの一つです。このブログでも何度か取り上げているのでご記憶の方も多いかなと。最近だと以下の記事で取り上げていますね。
ということで今回もこいつを使います。適当に前処理しておいたバージョンを僕のGitHubに置いてあるので、以下のようにしてRのワークスペースに読み込んでおきましょう*1。
# 男子 > dm<-read.csv('https://github.com/ozt-ca/tjo.hatenablog.samples/raw/master/r_samples/public_lib/jp/exp_uci_datasets/tennis/men.txt',header=T,sep='\t') # 女子 > dw<-read.csv('https://github.com/ozt-ca/tjo.hatenablog.samples/raw/master/r_samples/public_lib/jp/exp_uci_datasets/tennis/women.txt',header=T,sep='\t') # uninformativeな変数を除外する > dm<-dm[,-c(1,2,6,16,17,18,19,20,21,24,34,35,36,37,38,39)] > dw<-dw[,-c(1,2,6,16,17,18,19,20,21,24,34,35,36,37,38,39)]
これでinformativeな説明変数だけがdm, dwの2つのデータフレームに入ったはずです。
MXnetのDeep Learning (DNN)で男子のデータで学習し女子の結果を予測してみる
では、いよいよDeep Learningでテニス四大大会データセットの分類をやってみましょう。今回のデータセットは特に空間的な特徴を持っているわけではないので、DNNでやれば十分でしょう*2。冒頭に書いたように、今回使うのはMXnet。とりあえずデータの準備だけしておきましょう。
> library(mxnet) > train <- data.matrix(dm) > test <- data.matrix(dw) > train.x <- train[,-1] > train.y <- train[,1] > test.x <- test[,-1] > test.y <- test[,1]
これで、DNNのモデル部分を書いてmx.model.FeedForward.createメソッドで走らせればDNNを構築することができます。
何も考えずにMNISTの時と同様に特徴次元数×10, 特徴次元数×10, 特徴次元数×5の中間層2層でやってみる
MNISTをDNNで分類する場合は、概ねユニット数2400-2400-1200の中間層2層*3で回して良い結果が出ていたなぁというのを思い出したので、とりあえず「特徴次元数×10, 特徴次元数×10, 特徴次元数×5」のDNNでやってみます。ちなみにsoftmaxで出力しているので、手前のユニット数2の層は単なるまとめ層です。
> data <- mx.symbol.Variable("data") > fc1 <- mx.symbol.FullyConnected(data, name="fc1", num_hidden=220) > act1 <- mx.symbol.Activation(fc1, name="tanh1", act_type="tanh") > fc2 <- mx.symbol.FullyConnected(act1, name="fc2", num_hidden=220) > act2 <- mx.symbol.Activation(fc2, name="tanh2", act_type="tanh") > fc3 <- mx.symbol.FullyConnected(act2, name="fc3", num_hidden=110) > act3 <- mx.symbol.Activation(fc3, name="tanh3", act_type="tanh") > fc4 <- mx.symbol.FullyConnected(act3, name="fc4", num_hidden=2) > softmax <- mx.symbol.SoftmaxOutput(fc4, name="softmax") > devices <- mx.cpu() > mx.set.seed(71) > model <- mx.model.FeedForward.create(softmax, X=train.x, y=train.y, ctx=devices, num.round=100, array.batch.size=100, learning.rate=0.03, momentum=0.99, eval.metric=mx.metric.accuracy, initializer=mx.init.uniform(0.5), array.layout = "rowmajor", epoch.end.callback=mx.callback.log.train.metric(100)) Start training with 1 devices [1] Train-accuracy=0.5425 [2] Train-accuracy=0.618 [3] Train-accuracy=0.57 ... [99] Train-accuracy=0.502 [100] Train-accuracy=0.534 > preds <- predict(model, test.x, array.layout = "rowmajor") > pred.label <- max.col(t(preds)) - 1 > table(test.y, pred.label) pred.label test.y 1 0 227 1 225
あひゃひゃひゃひゃひゃ、全然ダメですorz しかも最初から最後までTrain-accuracyも0.5-0.6ぐらいでまるっきりうまくいってません。どうやらユニット数自体がそもそも不適切なようです。
特徴次元数×2, 特徴次元数×2, 特徴次元数×1の中間層2層DNNでやってみる
ユニット数が極端に多過ぎる気もするので、全部5分の1にまで減らしてみました。さぁどうでしょう。
> data <- mx.symbol.Variable("data") > fc1 <- mx.symbol.FullyConnected(data, name="fc1", num_hidden=46) > act1 <- mx.symbol.Activation(fc1, name="tanh1", act_type="tanh") > fc2 <- mx.symbol.FullyConnected(act1, name="fc2", num_hidden=46) > act2 <- mx.symbol.Activation(fc2, name="tanh2", act_type="tanh") > fc3 <- mx.symbol.FullyConnected(act2, name="fc3", num_hidden=23) > act3 <- mx.symbol.Activation(fc3, name="tanh3", act_type="tanh") > fc4 <- mx.symbol.FullyConnected(act3, name="fc4", num_hidden=2) > softmax <- mx.symbol.SoftmaxOutput(fc4, name="softmax") > devices <- mx.cpu() > mx.set.seed(71) > model <- mx.model.FeedForward.create(softmax, X=train.x, y=train.y, ctx=devices, num.round=100, array.batch.size=100, learning.rate=0.03, momentum=0.99, eval.metric=mx.metric.accuracy, initializer=mx.init.uniform(0.5), array.layout = "rowmajor", epoch.end.callback=mx.callback.log.train.metric(100)) Start training with 1 devices [1] Train-accuracy=0.535 [2] Train-accuracy=0.58 [3] Train-accuracy=0.61 [4] Train-accuracy=0.612 [5] Train-accuracy=0.666 [6] Train-accuracy=0.702 [7] Train-accuracy=0.72 [8] Train-accuracy=0.782 [9] Train-accuracy=0.838 [10] Train-accuracy=0.786 [11] Train-accuracy=0.778 [12] Train-accuracy=0.632 ... [99] Train-accuracy=0.51 [100] Train-accuracy=0.466 > preds <- predict(model, test.x, array.layout = "rowmajor") > pred.label <- max.col(t(preds)) - 1 > table(test.y, pred.label) pred.label test.y 0 0 227 1 225
これも全然ダメですねorz ただ、一つ気になったのがTrain-accuracyの変遷。どう見ても途中から過学習してる気がします。ということで、今度はepoch数を10前後にまで絞ってみましょう。ここは試行錯誤ということで。
> data <- mx.symbol.Variable("data") > fc1 <- mx.symbol.FullyConnected(data, name="fc1", num_hidden=46) > act1 <- mx.symbol.Activation(fc1, name="tanh1", act_type="tanh") > fc2 <- mx.symbol.FullyConnected(act1, name="fc2", num_hidden=46) > act2 <- mx.symbol.Activation(fc2, name="tanh2", act_type="tanh") > fc3 <- mx.symbol.FullyConnected(act2, name="fc3", num_hidden=23) > act3 <- mx.symbol.Activation(fc3, name="tanh3", act_type="tanh") > fc4 <- mx.symbol.FullyConnected(act3, name="fc4", num_hidden=2) > softmax <- mx.symbol.SoftmaxOutput(fc4, name="softmax") > devices <- mx.cpu() > mx.set.seed(71) > model <- mx.model.FeedForward.create(softmax, X=train.x, y=train.y, ctx=devices, num.round=9, array.batch.size=100, learning.rate=0.03, momentum=0.99, eval.metric=mx.metric.accuracy, initializer=mx.init.uniform(0.5), array.layout = "rowmajor", epoch.end.callback=mx.callback.log.train.metric(100)) Start training with 1 devices [1] Train-accuracy=0.535 [2] Train-accuracy=0.58 [3] Train-accuracy=0.61 [4] Train-accuracy=0.612 [5] Train-accuracy=0.666 [6] Train-accuracy=0.702 [7] Train-accuracy=0.72 [8] Train-accuracy=0.782 [9] Train-accuracy=0.838 > preds <- predict(model, test.x, array.layout = "rowmajor") > pred.label <- max.col(t(preds)) - 1 > table(test.y, pred.label) pred.label test.y 0 1 0 192 35 1 15 210 > sum(diag(table(test.y, pred.label)))/nrow(test) [1] 0.8893805
これでようやく分類器らしくなりました。Test-accuracyで0.889ならとりあえず分類できていると言って良いでしょう。
しばらくユニット数を変えてのたうち回ってみる
46-46-23で0.889になるのは分かったんですが、他の組み合わせだとどうなるんでしょうか? ここでは面倒なので結果だけ羅列していきますが、
- 46-23-23: 0.602
- 46-23-46: 0.867
- 46-46-46: 0.502
- 69-23-46: 0.520
- 46-23-8: 0.584
というように、これ以上やっても全くTest-accuracyが上がりませんorz 層数がダメなのかなぁ。。。
今度は中間層1層にしてみる
もしかしたら中間層多過ぎるかも?ということでさらに減らします。
- 46-23: 0.712
- 46-8: 0.861
- 32-8: 0.894
- 69-8: 0.825
- 30-30: 0.531
これもピンと来ないんだよなぁと。。。ちなみにこの時点で既にDeep LearningではなくてただのNNですorz
追記:尊敬するKaggler氏からのコメントに従ってデータを正規化してみた
この記事をupした段階で、僕も尊敬するKagglerの@toshi_k_datasciさんからこんなコメントをいただいたのでした。
@TJO_datasci mxnetは正規化処理(各変数平均0分散1にするとか)が必要なのではないでしょうか?
— toshi_k (@toshi_k_datasci) 2016年6月25日
@TJO_datasci 動きはするけど,それでは精度が全然出ないと思います.ちょっとやってみたのでご覧ください. https://t.co/cxVMx24vVh
— toshi_k (@toshi_k_datasci) 2016年6月25日
うわあああああああ、最近この辺真面目にやってないのですっかり怠ってましたorz 実際、黙っているとデフォルトで特徴量の正規化(scaling)をやってくれてしまうパッケージ・ライブラリって多いんですよね。。。*4ということでちゃんと正規化して回してみることにします。もちろん、正規化すると結果が変わるケースが非常に多いので他の試行錯誤のところもやり直してみました。
中間層が特徴次元数×10, 特徴次元数×10, 特徴次元数×5のケース
これは@toshi_k_datasciさんのスクリプトと完全に同じパターンですが、手元でやった結果も合わせて貼っておきます。まず前処理までのところ。
# 正規化する > train_means <- apply(train.x, 2, mean) > train_stds <- apply(train.x, 2, sd) > test_means <- apply(test.x, 2, mean) > test_stds <- apply(test.x, 2, sd) > train.x <- t((t(train.x)-train_means)/train_stds) > test.x <- t((t(test.x)-test_means)/test_stds)
これで@toshi_k_datasciさんのご指摘の通りに正規化ができました。では、実際に回してみましょう。
> data <- mx.symbol.Variable("data") > fc1 <- mx.symbol.FullyConnected(data, name="fc1", num_hidden=220) > act1 <- mx.symbol.Activation(fc1, name="tanh1", act_type="tanh") > fc2 <- mx.symbol.FullyConnected(act1, name="fc2", num_hidden=220) > act2 <- mx.symbol.Activation(fc2, name="tanh2", act_type="tanh") > fc3 <- mx.symbol.FullyConnected(act2, name="fc3", num_hidden=110) > act3 <- mx.symbol.Activation(fc3, name="tanh3", act_type="tanh") > fc4 <- mx.symbol.FullyConnected(act3, name="fc4", num_hidden=2) > softmax <- mx.symbol.SoftmaxOutput(fc4, name="softmax") > devices <- mx.cpu() > mx.set.seed(71) > model <- mx.model.FeedForward.create(softmax, X=train.x, y=train.y, ctx=devices, num.round=100, array.batch.size=100, learning.rate=0.03, momentum=0.99, eval.metric=mx.metric.accuracy, initializer=mx.init.uniform(0.5), array.layout = "rowmajor", epoch.end.callback=mx.callback.log.train.metric(100)) Start training with 1 devices [1] Train-accuracy=0.7375 [2] Train-accuracy=0.914 [3] Train-accuracy=0.952 [4] Train-accuracy=0.968 [5] Train-accuracy=0.98 [6] Train-accuracy=0.992 [7] Train-accuracy=1 [8] Train-accuracy=1 [9] Train-accuracy=0.998 [10] Train-accuracy=1 [11] Train-accuracy=1 ... [99] Train-accuracy=1 [100] Train-accuracy=1 > preds <- predict(model, test.x, array.layout = "rowmajor") > pred.label <- max.col(t(preds)) - 1 > table(test.y, pred.label) pred.label test.y 0 1 0 209 18 1 19 206 > sum(diag(table(test.y, pred.label)))/nrow(dw) [1] 0.9181416
Test-accuracyが0.918と圧倒的に良くなりました。正規化前だと全く学習せずに0.5の行進が続いていたのを考えるとウソのようです。ただ、途中で過学習している気がするので早期打ち切りを兼ねてepoch数を10まで減らしてみます。
> data <- mx.symbol.Variable("data") > fc1 <- mx.symbol.FullyConnected(data, name="fc1", num_hidden=220) > act1 <- mx.symbol.Activation(fc1, name="tanh1", act_type="tanh") > fc2 <- mx.symbol.FullyConnected(act1, name="fc2", num_hidden=220) > act2 <- mx.symbol.Activation(fc2, name="tanh2", act_type="tanh") > fc3 <- mx.symbol.FullyConnected(act2, name="fc3", num_hidden=110) > act3 <- mx.symbol.Activation(fc3, name="tanh3", act_type="tanh") > fc4 <- mx.symbol.FullyConnected(act3, name="fc4", num_hidden=2) > softmax <- mx.symbol.SoftmaxOutput(fc4, name="softmax") > devices <- mx.cpu() > mx.set.seed(71) > model <- mx.model.FeedForward.create(softmax, X=train.x, y=train.y, ctx=devices, num.round=10, array.batch.size=100, learning.rate=0.03, momentum=0.99, eval.metric=mx.metric.accuracy, initializer=mx.init.uniform(0.5), array.layout = "rowmajor", epoch.end.callback=mx.callback.log.train.metric(100)) Start training with 1 devices [1] Train-accuracy=0.7375 [2] Train-accuracy=0.914 [3] Train-accuracy=0.952 [4] Train-accuracy=0.968 [5] Train-accuracy=0.98 [6] Train-accuracy=0.992 [7] Train-accuracy=1 [8] Train-accuracy=1 [9] Train-accuracy=0.998 [10] Train-accuracy=1 > preds <- predict(model, test.x, array.layout = "rowmajor") > pred.label <- max.col(t(preds)) - 1 > table(test.y, pred.label) pred.label test.y 0 1 0 213 14 1 21 204 > sum(diag(table(test.y, pred.label)))/nrow(dw) [1] 0.9225664
Test-accuracyが0.923まで向上しました。ここまで来ればとりあえずOKかなと。
特徴次元数×2, 特徴次元数×2, 特徴次元数×1でやってみる
既に上の方で試したように、やはりユニット数が多いのではないかと思われるので5分の1まで減らしてみました。
> data <- mx.symbol.Variable("data") > fc1 <- mx.symbol.FullyConnected(data, name="fc1", num_hidden=46) > act1 <- mx.symbol.Activation(fc1, name="tanh1", act_type="tanh") > fc2 <- mx.symbol.FullyConnected(act1, name="fc2", num_hidden=46) > act2 <- mx.symbol.Activation(fc2, name="tanh2", act_type="tanh") > fc3 <- mx.symbol.FullyConnected(act2, name="fc3", num_hidden=23) > act3 <- mx.symbol.Activation(fc3, name="tanh3", act_type="tanh") > fc4 <- mx.symbol.FullyConnected(act3, name="fc4", num_hidden=2) > softmax <- mx.symbol.SoftmaxOutput(fc4, name="softmax") > devices <- mx.cpu() > mx.set.seed(71) > model <- mx.model.FeedForward.create(softmax, X=train.x, y=train.y, ctx=devices, num.round=30, array.batch.size=100, learning.rate=0.03, momentum=0.99, eval.metric=mx.metric.accuracy, initializer=mx.init.uniform(0.5), array.layout = "rowmajor", epoch.end.callback=mx.callback.log.train.metric(100)) Start training with 1 devices [1] Train-accuracy=0.66 [2] Train-accuracy=0.814 [3] Train-accuracy=0.864 [4] Train-accuracy=0.902 [5] Train-accuracy=0.904 [6] Train-accuracy=0.932 [7] Train-accuracy=0.934 [8] Train-accuracy=0.954 [9] Train-accuracy=0.944 [10] Train-accuracy=0.952 [11] Train-accuracy=0.958 [12] Train-accuracy=0.962 [13] Train-accuracy=0.964 [14] Train-accuracy=0.976 [15] Train-accuracy=0.976 [16] Train-accuracy=0.976 [17] Train-accuracy=0.976 [18] Train-accuracy=0.982 [19] Train-accuracy=0.982 [20] Train-accuracy=0.99 [21] Train-accuracy=0.994 [22] Train-accuracy=0.994 [23] Train-accuracy=0.996 [24] Train-accuracy=0.994 [25] Train-accuracy=0.998 [26] Train-accuracy=1 [27] Train-accuracy=1 [28] Train-accuracy=1 [29] Train-accuracy=1 [30] Train-accuracy=1 > preds <- predict(model, test.x, array.layout = "rowmajor") > pred.label <- max.col(t(preds)) - 1 > table(test.y, pred.label) pred.label test.y 0 1 0 211 16 1 18 207 > sum(diag(table(test.y, pred.label)))/nrow(dw) [1] 0.9247788
Test accuracyが0.925まで上がってきました。これなら十分な精度と言えるでしょう。ちなみにその他のユニット数のケースでも同様に試してみましたが、Test accuracy 0.925を超えた設定はありませんでした。ただし、どれでも必ずTest accuracy 0.900を超えるようになってきたので、やはり正規化することできちんとDNNがworkしていることがうかがえます。
他の分類器と比べてみる
6月15日に秋葉原で講演した時に実は種明かしをしたんですが、要はこの手のアスリートの勝敗とmatch statsとの関係性って結構シンプルで、「勝った方がより効率的&負けた方がより非効率的」な変数だらけなんですよね。なので、このテニス四大大会データセットも事実上線形分離可能パターンとして振舞います。よってベストスコアを叩き出すのはL1正則化ロジスティック回帰もしくは線形SVMであることが既に分かっていて、試しにやってみるとこうなります。
# L1正則化ロジスティック回帰 > library(glmnet) > dm.l1 <- cv.glmnet(as.matrix(dm[,-1]), as.matrix(dm[,1]), family='binomial', alpha=1) > table(dw$Result, round(predict(dm.l1, newx=as.matrix(dw[,-1]), type='response', s=dm.l1$lambda.min),0)) 0 1 0 215 12 1 18 207 > sum(diag(table(dw$Result, round(predict(dm.l1, newx=as.matrix(dw[,-1]), type='response', s=dm.l1$lambda.min),0))))/nrow(dw) [1] 0.9336283
Test-accuracy 0.934で上でMXnetで頑張って試した全てのDNNのスコアを上回っていますorz
# 線形SVM > library(e1071) > dm.svm.l <- svm(as.factor(Result)~., dm, kernel='linear') > table(dw$Result, predict(dm.svm.l, newdata=dw[,-1])) 0 1 0 214 13 1 16 209 > sum(diag(table(dw$Result, predict(dm.svm.l, newdata=dw[,-1]))))/nrow(dw) [1] 0.9358407
Test-accuracy 0.936で、もちろん全てのDNNを上回っていますorz ということで、テニス四大大会データセットに対してはDeep Learning (DNN)で臨むよりもL1正則化ロジスティック回帰や線形SVMといった古典的な線形分類器で臨んだ方がパフォーマンスが良いということが分かりました。
ついでに線形分離可能パターン2次元データに対する振舞いを見てみる
と、ここまででDNNの線形分離可能パターン(不可能パターンではない)に対する挙動に疑念が生じてきたので、ちょっとやってみました。設定としては4-3-3のDNNで、スクリプトは以下の通りです。
# データをインポートして、MXnetに読ませるための下処理と、プロット周りをグリッド含めて準備しておく > dbi <- read.csv('https://github.com/ozt-ca/tjo.hatenablog.samples/raw/master/r_samples/public_lib/jp/dbi_large.txt', header=T, sep='\t') > dbi$label <- dbi$label-1 > px <- seq(-4,4,0.03) > py <- seq(-4,4,0.03) > pgrid <- expand.grid(px,py) > names(pgrid) <- names(dbi)[-3] > dbi_train <- data.matrix(dbi) > dbi_train.x <- dbi_train[,-3] > dbi_train.y <- dbi_train[,3] > dbi_test <- data.matrix(pgrid) > label_grid <- rep(0, nrow(pgrid)) > for (i in 1:nrow(pgrid)){ + if (pgrid[i,1]+pgrid[i,2]<0){label_grid[i] <- 1} + } # MXnetで4-3-3中間層2層のDNNを回す > data <- mx.symbol.Variable("data") > fc1 <- mx.symbol.FullyConnected(data, name="fc1", num_hidden=4) > act1 <- mx.symbol.Activation(fc1, name="tanh1", act_type="tanh") > fc2 <- mx.symbol.FullyConnected(act1, name="fc2", num_hidden=3) > act2 <- mx.symbol.Activation(fc2, name="tanh2", act_type="tanh") > fc3 <- mx.symbol.FullyConnected(act2, name="fc3", num_hidden=3) > act3 <- mx.symbol.Activation(fc3, name="tanh3", act_type="tanh") > fc4 <- mx.symbol.FullyConnected(act3, name="fc4", num_hidden=2) > softmax <- mx.symbol.SoftmaxOutput(fc4, name="softmax") > devices <- mx.cpu() > mx.set.seed(71) > model <- mx.model.FeedForward.create(softmax, X=dbi_train.x, y=dbi_train.y, ctx=devices, num.round=20, array.batch.size=100, learning.rate=0.03, momentum=0.99, eval.metric=mx.metric.accuracy, initializer=mx.init.uniform(0.5), array.layout = "rowmajor", epoch.end.callback=mx.callback.log.train.metric(100)) Start training with 1 devices [1] Train-accuracy=0.944848484848485 ... [20] Train-accuracy=0.9479 > preds <- predict(model, dbi_test, array.layout = "rowmajor") > pred.label <- max.col(t(preds)) - 1 > table(label_grid, pred.label) pred.label label_grid 0 1 0 33157 2354 1 287 35491 > sum(diag(table(label_grid, pred.label)))/nrow(pgrid) [1] 0.9629536 # 描画する > plot(c(), type='n', xlim=c(-4,4), ylim=c(-4,4), xlab='', ylab='') > par(new=T) > polygon(c(-4,4,4),c(4,-4,4),col='#dddddd') > par(new=T) > polygon(c(-4,-4,4),c(4,-4,-4),col='#ffdddd') > par(new=T) > plot(dbi[,-3], pch=19, cex=0.5, col=dbi$label+1, xlim=c(-4,4), ylim=c(-4,4), xlab='', ylab='') > par(new=T) > contour(px, py, array(pred.label, dim=c(length(px),length(py))), col='purple', lwd=5, levels =0.5, drawlabels=F, xlim=c(-4,4), ylim=c(-4,4))
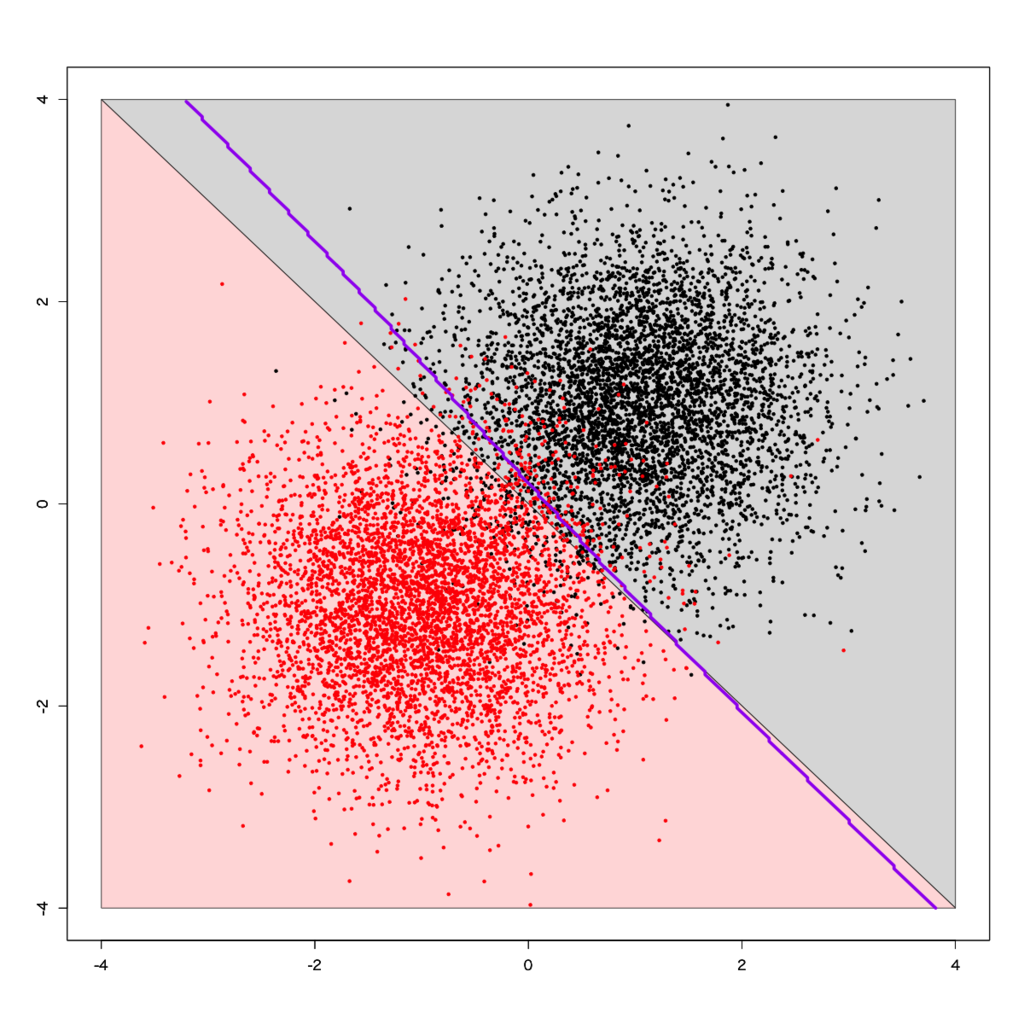
これなら良さそうに見えます。真のクラス境界に対するTest-accuracyも0.963と悪くありません。では極端なDNN、例えば200-200-100という設定で組んでみるとどうなるんでしょうか?
> data <- mx.symbol.Variable("data") > fc1 <- mx.symbol.FullyConnected(data, name="fc1", num_hidden=200) > act1 <- mx.symbol.Activation(fc1, name="tanh1", act_type="tanh") > fc2 <- mx.symbol.FullyConnected(act1, name="fc2", num_hidden=200) > act2 <- mx.symbol.Activation(fc2, name="tanh2", act_type="tanh") > fc3 <- mx.symbol.FullyConnected(act2, name="fc3", num_hidden=100) > act3 <- mx.symbol.Activation(fc3, name="tanh3", act_type="tanh") > fc4 <- mx.symbol.FullyConnected(act3, name="fc4", num_hidden=2) > softmax <- mx.symbol.SoftmaxOutput(fc4, name="softmax") > devices <- mx.cpu() > mx.set.seed(71) > model <- mx.model.FeedForward.create(softmax, X=dbi_train.x, y=dbi_train.y, ctx=devices, num.round=20, array.batch.size=100, learning.rate=0.03, momentum=0.99, eval.metric=mx.metric.accuracy, initializer=mx.init.uniform(0.5), array.layout = "rowmajor", epoch.end.callback=mx.callback.log.train.metric(100)) Start training with 1 devices [1] Train-accuracy=0.935656565656566 [2] Train-accuracy=0.938 [3] Train-accuracy=0.9425 [4] Train-accuracy=0.939 [5] Train-accuracy=0.9352 [6] Train-accuracy=0.9379 [7] Train-accuracy=0.936300000000001 [8] Train-accuracy=0.938000000000001 [9] Train-accuracy=0.9439 [10] Train-accuracy=0.9343 [11] Train-accuracy=0.9426 [12] Train-accuracy=0.9412 [13] Train-accuracy=0.9389 [14] Train-accuracy=0.9372 [15] Train-accuracy=0.9372 [16] Train-accuracy=0.9385 [17] Train-accuracy=0.941000000000001 [18] Train-accuracy=0.937900000000001 [19] Train-accuracy=0.9419 [20] Train-accuracy=0.9371 > preds <- predict(model, dbi_test, array.layout = "rowmajor") > pred.label <- max.col(t(preds)) - 1 > table(label_grid, pred.label) pred.label label_grid 0 1 0 28881 6630 1 6 35772 > sum(diag(table(label_grid, pred.label)))/nrow(pgrid) [1] 0.9069141 > plot(c(), type='n', xlim=c(-4,4), ylim=c(-4,4), xlab='', ylab='') > par(new=T) > polygon(c(-4,4,4),c(4,-4,4),col='#dddddd') > par(new=T) > polygon(c(-4,-4,4),c(4,-4,-4),col='#ffdddd') > par(new=T) > plot(dbi[,-3], pch=19, cex=0.5, col=dbi$label+1, xlim=c(-4,4), ylim=c(-4,4), xlab='', ylab='') > par(new=T) > contour(px, py, array(pred.label, dim=c(length(px),length(py))), col='purple', lwd=5, levels =0.5, drawlabels=F, xlim=c(-4,4), ylim=c(-4,4))

ある意味予想通りですが、変なところで過学習をしていて奇妙な決定境界を描いています。実際、真のクラス境界に対するTest-accuracyも0.907にまで悪化しています。
DNNに限らず、Deep Learningを組む時にフレームワークを使っていると何となく「とりあえずユニット数大きくしとくか〜」みたいな気分で設定してしまいがちですが、根拠もなくユニット数を大きくすると過学習するかも?という可能性が、前半のテニス四大大会データセット・後半の線形分離可能2次元パターンの結果からはうかがわれます。
この辺のポイントに注意しながら、次回以降も色々データセットを替えてやってみようかなと思います。
追記部分も含めた上での感想
上記のように途中で@toshi_k_datasciさんからのご指摘に従ってちゃんと正規化してみたら確かにパフォーマンスがグッと向上したわけで、「はじパタ」にも「カステラ本」にも果ては「黄色い本」ことPRMLにも「特徴量は必ず正規化しやがれコノヤロウ」と書いてあるのにはちゃんと理由があるんだなぁと再確認いたしましたorz そう、LIBSVM(上記の線形SVMである{e1071}の本体)もデフォルトでデータの正規化をしてるんですよね。。。そりゃあ正規化なしで比較するのは不公平でしょと。
ただ、それで規定通りのパフォーマンスに達したDNNであっても、今回のテニス四大大会データセットに対してはL1正則化ロジスティック回帰&線形SVMのような線形分類器に対して及ばなかったわけで、それこそがDNNの使いどころの難しい点なのかなとも思った次第です。
ということで、とりあえず何がなくともMXnetだろうとKerasだろうとDeep Learningフレームワーク使う時は正規化というかスケーリング忘れずにやるようにしますorz 良き教訓を得た週末でございました。