以前「Ads carryover & shape effects付きのMedia Mix Modeling」という記事で取り上げたベイジアンMMMのtechnical report (Jin et al., 2017)ですが、当時RStanで実装されていたものが4年の時を経て時代の趨勢に沿う形でPythonベースのOSSとしてリリースされています。
それがLightweight MMM (LMMM)です。ベイジアンモデリング部分はNumPyroによるMCMCサンプラーで実装されており、さらにはモダンなMMMフレームワークにおいて標準的とされる予算配分の最適化ルーチンも実装されています。全体的な使い勝手としては、まだ開発途上の部分もあるので時々痒いところに手が届かない感があるものの、概ねRStanで実装したものと似たような感じに仕上がっているという印象です。
ということで、LMMMがどんな感じで動くかを簡単に紹介してみようと思います。基本的にはGitHub上のdemoに沿った話題に留まりますが、復習も兼ねてベイジアンMMMの仕組みについても簡単に触れていくつもりです。
Disclosure of conflicts of interest
LMMMの開発チームとid:TJOは同じ企業に所属しています。また、Colaboratory (Colab)はその所属企業のプロダクトです。
ベイジアンMMMの主要なポイント
ぶっちゃけ主な仕様はソースコードを見れば大体分かるかと思いますし、NumPyroの方がStanでコードを読むより分かりやすいという印象があります。とは言え、初めての人もいるかと思いますので簡単におさらいとしてベイジアンMMMの特徴をまとめておきます。
Adstock(広告効果の時間遅れ)
単純に言えば読んで字の如く「人々の目に広告が触れた後でタイムラグが生じたり減衰しながら持続する広告効果」をモデリングするものです。Jin et al. (2017)では以下のように定義しています。
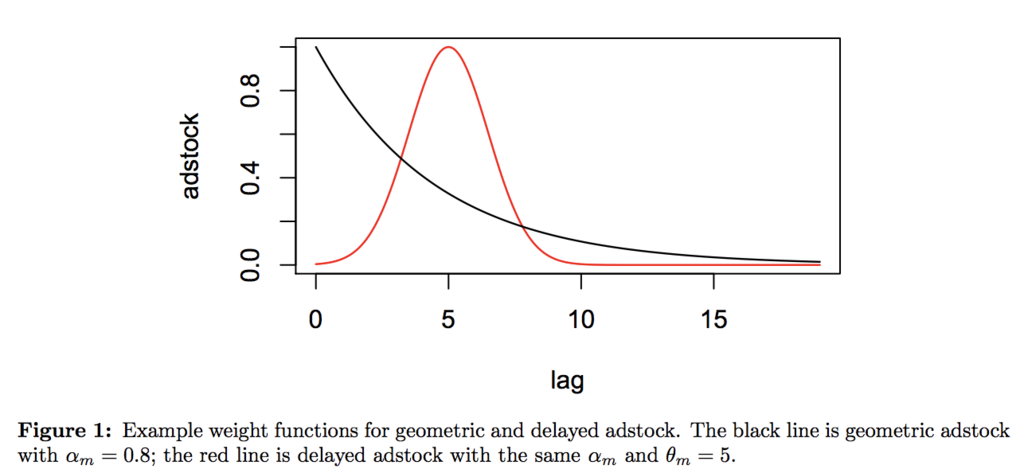
当然ですが、ハイパーパラメータを変えることでロングテールにしたりピークまでのタイムラグを変えることが可能ですし、さらにそのハイパーパラメータの事前分布を適切に定めることである程度データに合わせて自動的にadstockの形状を決めることもできます。
Response curve(広告効果の飽和)
これは「広告接触が過剰になると効果が飽和する」という話で、Jin et al. (2017)では薬理学における薬品の血中濃度モデルを援用して広告効果が飽和する様子を以下のようにモデリングしています。

図を見ての通りで、「徐々に傾きが0に近づいていく」S字カーブを描くことになります。これはタイムポイントごとの広告出稿額(例えば日次のTVCM出稿額)に対してプロットできるので、例えばその変曲点より手前に日次出稿額の点が集中するようなら「まだ飽和していないのでもっと日次の出稿額を上げるべき」というような判断ができることになります。これもハイパーパラメータで形状が変えられますし、事前分布を使って自動的に決定することもできます。
最終的なモデル
目的変数に対して、上記のadstockとresponse curveを加味したメディア変数とそのパラメータ
による回帰モデルと、非メディア変数
とそのパラメータ
による回帰モデルと、切片と季節調整とトレンドと誤差項を足し合わせたJin et al. (2017)の式(7)が最終的なモデル表現となります。これに事前分布を含めたハイパーパラメータを与えてやり、各パラメータをMCMCサンプリングでベイズ推定するというのがベイジアンMMMの流れです。モデル(パラメータ)が求まれば、そこから逆算して個々のメディア変数(広告)がどれくらい目的変数(売上高など)に貢献しているかも算出できますし、勿論その値を投下総額で割り戻せばROI (ROAS)も求まります。
そして、得られたを初めとするパラメータに基づいて、適切に最適化計画を解けば最適な予算配分を求めることも可能です。特にJin et al. (2017)ではadstockとresponse curveも掛け合わせることでよりメディアごとの特性に即した最適化を行っています。
MMMをベイジアンモデリングで推定する利点
最大のメリットは「全てのパラメータ推定をMCMCによるベイジアンモデリングを通じて『互いに同時にバランスを取って』行うことができる」点と言って良いかと思います。というのは、過去現在の様々なMMMの手法では例えばadstockなど各種の非線形成分を「事前に決め打ちで推定」しておいて「後から数値解析的に最適解を探索する」ものがあったりするんですが、このやり方だとメモリを食い過ぎる上にパラメータ探索のやり方次第では本来の最適なパラメータの組み合わせを見逃す可能性があります。
これに対して、MCMCによるベイジアンモデリングで一括して全パラメータを同時に推定する(事後分布をサンプリングする)と、最初からいきなり本来の最適なパラメータの組み合わせを探索しに行ける(しかも互いに同時にバランスが取られている)というメリットが得られます。勿論MCMCサンプリングの収束が悪ければ別の問題が色々発生し得るわけですが、そのデメリットを上回る利便性があると言って良いでしょう。
LMMMの実践例
それでは、実際にLMMMはどのように動くかを見てみましょう。一応、dependenciesのversion conflictとかが面倒だったのもあってpublic Colabで全部書いてみました。基本的にはexamplesに置かれているsimple end-to-end demoをほぼそのまま実行した結果をただ並べただけですので、難しいことは何もありません。とは言え、初めてベイジアンMMMに触れる人には見慣れない箇所も多いかもしれませんので、順を追って説明していきます。
インストール
pip install --upgrade pip pip install lightweight_mmm
LMMM自体はpipで入ります。ただし、環境によってdependenciesごとにversion conflictを起こすことがあるので要注意です。Colabでやった時は何とmatplotlibがconflictを起こしたので、改めて最新版をインストールしています。
パッケージ・モジュールのインポート
ここからはColab (notebook)と対応させながら説明していきます。まず、必要なパッケージ・モジュールをインポートします。先にjax.numpyとnumpyroを読み込みます。
import jax.numpy as jnp import numpyro
それからLMMMの各モジュールをインポートします。
from lightweight_mmm import lightweight_mmm from lightweight_mmm import optimize_media from lightweight_mmm import plot from lightweight_mmm import preprocessing from lightweight_mmm import utils
これで準備完了です。
データセットの読み込み(ダミーデータ生成)
公式のdemoに沿って、ここではダミーデータを生成します。最初にシード値を決めておきます。71なのは幾星霜も前からの習わしです(笑)。
SEED = 71
LMMMはデフォルトではweekly(52週の季節調整を伴う)で動くようになっていて、ダミーデータを生成するutilsの関数もweeklyでしか動かないので、ここではweeklyデータとします。サンプルサイズは学習データを2年(104週)+交差検証データ(OOS)を1四半期(13週)とし、メディア変数は5個、非メディア変数(例えば競合のキャンペーンなど)は1個とします。
data_size = 104 + 13 n_media_channels = 5 n_extra_features = 1
後はutils.simulate_dummy_dataにこれらの値を与えればおしまいです。
media_data, extra_features, target, costs = utils.simulate_dummy_data(
data_size=data_size,
n_media_channels=n_media_channels,
n_extra_features=n_extra_features)
得られるのはmedia_data, extra_features, target, costsの4種類の変数で、実データを与える場合もこれを踏襲する必要があります。
- Media data: Containing the metric per channel and time span (eg. impressions per time period). Media values must not contain negative values.
- Extra features: Any other features that one might want to add to the analysis. These features need to be known ahead of time for optimization or you would need another model to estimate them.
- Target: Target KPI for the model to predict. For example, revenue amount, number of app installs. This will also be the metric optimized during the optimization phase.
- Costs: The total cost per media unit per channel.
もう少し具体的に書いておくと、基本的にどの変数もjax.numpyのDeviceArray。media_dataはメディア広告の出稿に関する指標(GRPなどのボリューム指標でも出稿金額でも基本的には大丈夫)から成るメディア変数、extra_featuresは気温*1やキャンペーンの有無といった広告以外の指標から成る非メディア変数、targetは売上高や契約件数といったKPIつまり目的変数で、costsは個々のメディア広告の分析期間内の総額です。
ちなみにメディア変数の個数をmm, 非メディア変数の個数をme, サンプルサイズをNとすると、それぞれの変数の次元はmedia_data: N x mm, extra_features: N x me, target: N x 1, costs: 1 x mm, となります。
次にデータセットを学習データ(Train)と交差検証データ(OOS)とに分けていきます。この作業は3つのデータ変数それぞれに対して行う必要があります。
# Split and scale data. split_point = data_size - 13 # Media data media_data_train = media_data[:split_point, ...] media_data_test = media_data[split_point:, ...] # Extra features extra_features_train = extra_features[:split_point, ...] extra_features_test = extra_features[split_point:, ...] # Target target_train = target[:split_point]
さらに前処理としてスケーリングを行います。
media_scaler = preprocessing.CustomScaler(divide_operation=jnp.mean)
extra_features_scaler = preprocessing.CustomScaler(divide_operation=jnp.mean)
target_scaler = preprocessing.CustomScaler(divide_operation=jnp.mean)
cost_scaler = preprocessing.CustomScaler(divide_operation=jnp.mean, multiply_by=0.15)
media_data_train = media_scaler.fit_transform(media_data_train)
extra_features_train = extra_features_scaler.fit_transform(extra_features_train)
target_train = target_scaler.fit_transform(target_train)
costs = cost_scaler.fit_transform(costs)
これでデータセットも揃いました。
モデル推定(MCMCサンプリング)
ここからはいよいよMCMCサンプリングによるモデル推定です。まず、LightweightMMMクラスオブジェクトを用意します。
mmm = lightweight_mmm.LightweightMMM(model_name="carryover")
次に、MCMCサンプリングのサイズを決めます。元のdemoではwarmupもsamplesも1000に設定されています。
number_warmup=1000 number_samples=1000
後は、fitメソッドでMCMCサンプリングするだけです。ちなみにfitの引数にweekday_seasonality (Boolean)とseasonality_frequencyとがあってdailyとweeklyとを切り替えることができます。
mmm.fit(
media=media_data_train,
media_prior=costs,
target=target_train,
extra_features=extra_features_train,
number_warmup=number_warmup,
number_samples=number_samples,
seed=SEED)
/usr/local/lib/python3.7/dist-packages/lightweight_mmm/lightweight_mmm.py:256: UserWarning: There are not enough devices to run parallel chains: expected 2 but got 1. Chains will be drawn sequentially. If you are running MCMC in CPU, consider using `numpyro.set_host_device_count(2)` at the beginning of your program. You can double-check how many devices are available in your system using `jax.local_device_count()`. num_chains=number_chains) sample: 100%|██████████| 2000/2000 [04:24<00:00, 7.55it/s, 1023 steps of size 1.37e-03. acc. prob=0.92] sample: 100%|██████████| 2000/2000 [04:13<00:00, 7.90it/s, 507 steps of size 1.46e-03. acc. prob=0.91]
モデルのチェック
ベイジアンモデルなので、MCMCサンプリングが適切に収束したかどうかをチェックする必要があります。
mmm.print_summary()
mean std median 5.0% 95.0% n_eff r_hat
ad_effect_retention_rate[0] 0.44 0.28 0.42 0.00 0.87 287.02 1.01
ad_effect_retention_rate[1] 0.28 0.15 0.27 0.02 0.52 298.63 1.00
ad_effect_retention_rate[2] 0.47 0.29 0.46 0.00 0.87 302.86 1.01
ad_effect_retention_rate[3] 0.43 0.28 0.41 0.00 0.83 452.40 1.00
ad_effect_retention_rate[4] 0.34 0.24 0.30 0.00 0.69 197.75 1.01
coef_extra_features[0] 0.01 0.01 0.01 -0.00 0.02 364.91 1.02
coef_media[0] 0.02 0.02 0.01 0.00 0.04 280.71 1.00
coef_media[1] 0.15 0.03 0.15 0.10 0.20 282.27 1.01
coef_media[2] 0.01 0.01 0.01 0.00 0.03 304.08 1.00
coef_media[3] 0.01 0.01 0.01 0.00 0.03 283.34 1.01
coef_media[4] 0.05 0.03 0.04 0.00 0.09 276.95 1.01
coef_trend[0] -0.00 0.00 -0.00 -0.00 0.00 405.10 1.01
expo_trend 0.68 0.18 0.62 0.50 0.94 269.67 1.01
exponent[0] 0.89 0.09 0.92 0.77 1.00 372.92 1.00
exponent[1] 0.92 0.07 0.94 0.82 1.00 327.43 1.01
exponent[2] 0.89 0.10 0.92 0.75 1.00 549.61 1.00
exponent[3] 0.89 0.10 0.91 0.75 1.00 433.51 1.00
exponent[4] 0.91 0.08 0.93 0.80 1.00 520.83 1.00
gamma_seasonality[0,0] -0.07 1.00 -0.08 -1.71 1.54 223.15 1.01
gamma_seasonality[0,1] -0.21 0.61 -0.15 -1.19 0.73 111.39 1.02
gamma_seasonality[1,0] -0.01 0.00 -0.01 -0.02 -0.01 652.54 1.00
gamma_seasonality[1,1] -0.00 0.00 -0.00 -0.00 0.00 1034.95 1.00
intercept[0] 0.97 0.60 0.90 0.00 1.86 112.29 1.03
peak_effect_delay[0] 0.92 0.96 0.59 0.00 2.23 346.35 1.00
peak_effect_delay[1] 0.23 0.14 0.22 0.00 0.43 278.50 1.00
peak_effect_delay[2] 1.08 1.07 0.70 0.00 2.57 345.97 1.00
peak_effect_delay[3] 1.07 1.09 0.70 0.00 2.53 318.55 1.01
peak_effect_delay[4] 0.49 0.59 0.31 0.00 1.07 176.97 1.02
sigma[0] 0.02 0.00 0.02 0.01 0.02 308.08 1.00
Number of divergences: 42差し当たり重要なのはr_hatで、これがいずれも1.00付近であれば収束していると判断して差し支えないです。一方で、どれかのパラメータで1.1以上になる場合は、収束していない可能性があるためモデルを再考する必要があるかもしれません。パラメータの事後分布をプロットして確かめることもできます。
plot.plot_media_channel_posteriors(media_mix_model=mmm)
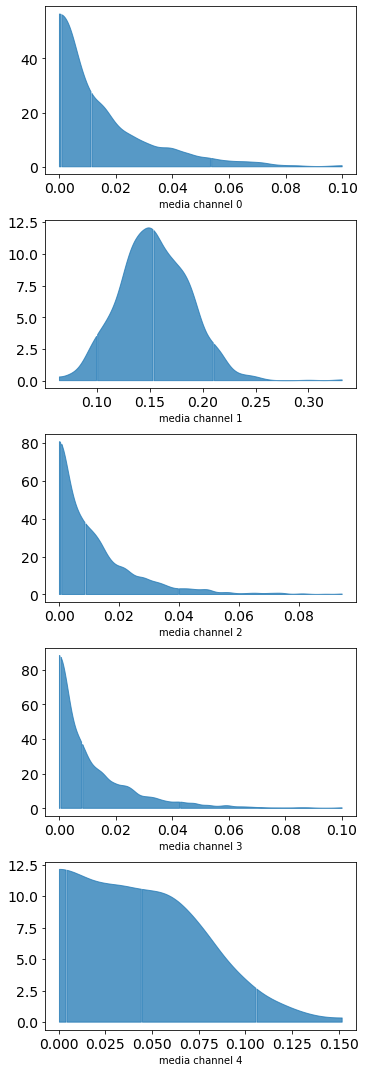
一般にMMMはメディアパラメータを非負、つまり切断(半)正規分布とみなすことが多いので、得られた事後分布もそれっぽくなっています。このため平均や中央値などで代表値を得る際には注意が必要です。
モデル評価
ベイジアンMMMは統計モデルであり、そうである以上モデル性能の評価が必ず求められます。特に理由がない限りは、学習データへの当てはまりと、交差検証データ(OOS)への当てはまり即ち汎化性能の2点を原則としてチェックすることになります。まず、前者をプロットしてみます。
plot.plot_model_fit(mmm, target_scaler=target_scaler)
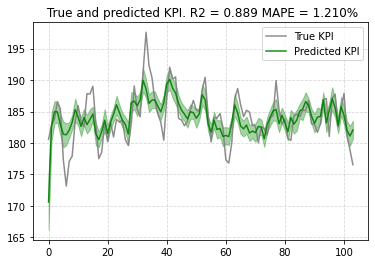
多少外れている部分もあるようですが、MAPE(平均絶対パーセンテージ誤差)を見る限りでは悪くなさそうです。OOSへの当てはまりもプロットしてみましょう。
new_predictions = mmm.predict(media=media_scaler.transform(media_data_test),
extra_features=extra_features_scaler.transform(extra_features_test),
seed=SEED)
new_predictions.shape
(2000, 13)
plot.plot_out_of_sample_model_fit(out_of_sample_predictions=new_predictions,
out_of_sample_target=target_scaler.transform(target[split_point:]))
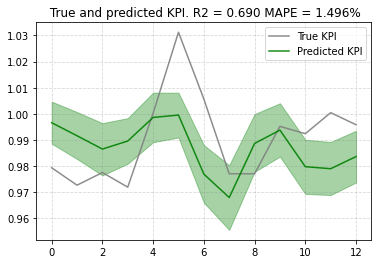
これもMAPEを見る限りでは悪くないように思われます。ただ、汎化性能の評価は「複数モデル間で比較して初めて意味がある」ものなので、原則として2つ以上のモデルを常に用意して、互いに比べる必要があります。もっともMMMを実施する場合はあまりモデルの選択肢がないことも多いので、事前に許容可能なMAPEの最大値を決めておく(例えば「20%」など)という実務的なやり方もあり得ます。
モデル解釈(メディア変数に関する知見)
ここからがベイジアンMMM最大の目的である、モデル解釈のパートです。まず、メディア変数ごとの期間全体に占める「貢献度」(目的変数に対する)の時系列をプロットしてみます。
plot.plot_media_baseline_contribution_area_plot(media_mix_model=mmm,
target_scaler=target_scaler,
fig_size=(30,10))
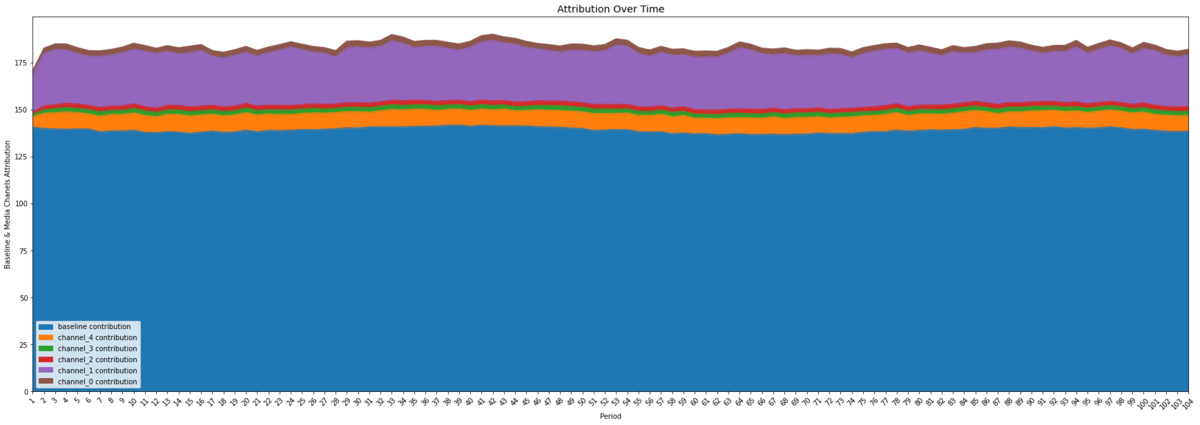
次に、期間全体をまたいだメディア変数ごとの「貢献度」と、ROI (ROAS)を算出します。
media_contribution, roi_hat = mmm.get_posterior_metrics(target_scaler=target_scaler, cost_scaler=cost_scaler)
「貢献度」を棒プロットにしてみます。
plot.plot_bars_media_metrics(metric=media_contribution, metric_name="Media Contribution Percentage")
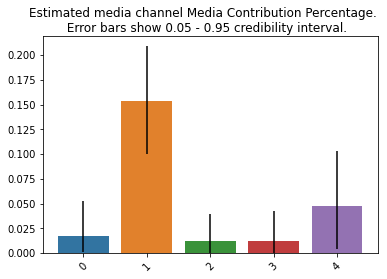
ROI (ROAS)も棒プロットにしてみます。
plot.plot_bars_media_metrics(metric=roi_hat, metric_name="ROI hat")
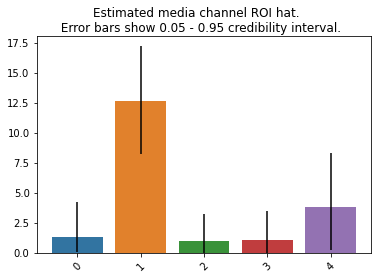
Response curveもプロットできます。本来ならS字カーブを描くはずなんですが……。
plot.plot_response_curves(
media_mix_model=mmm, target_scaler=target_scaler, seed=SEED)
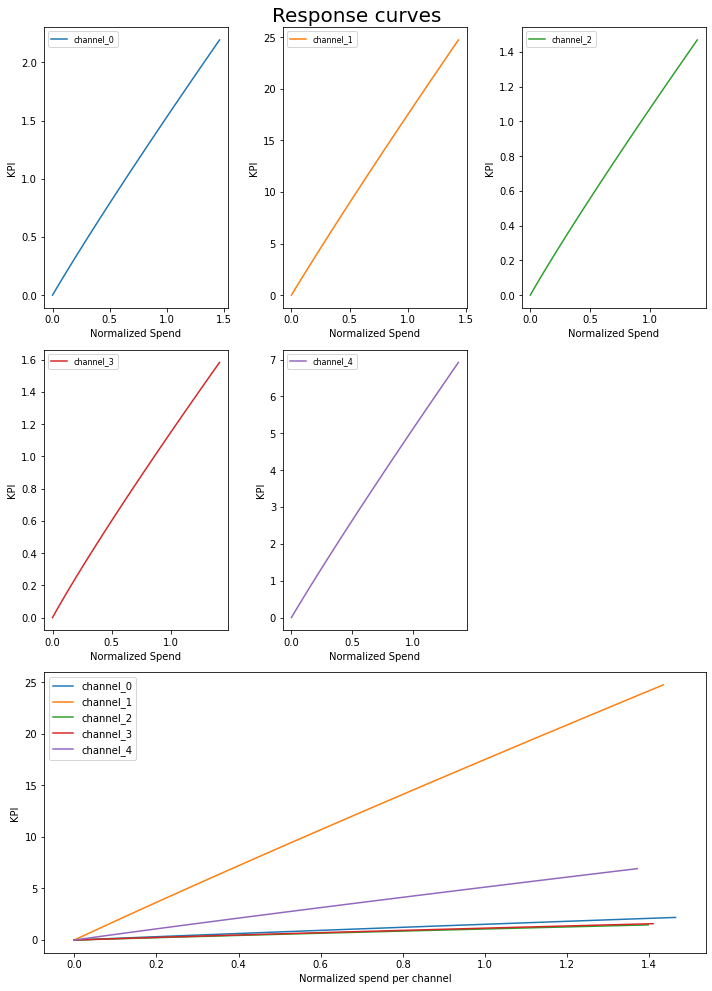
メディア予算の最適配分
最後に、メディア予算の最適配分を求めます。ちなみにoptimize_media.pyを見ると、scipy.optimizeのminimize(method=’SLSQP’)を用いて逐次二次計画法による最適化が行われていることが分かります。まず、最適化計画のためのデータセットを作ります。
prices = jnp.ones(mmm.n_media_channels) n_time_periods = 10 budget = jnp.sum(jnp.dot(prices, media_data.mean(axis=0)))* n_time_periods
そして、最適化計画をソルバを用いて解きます。
# Run optimization with the parameters of choice.
solution, kpi_without_optim, previous_budget_allocation = optimize_media.find_optimal_budgets(
n_time_periods=n_time_periods,
media_mix_model=mmm,
extra_features=extra_features_scaler.transform(extra_features_test)[:n_time_periods],
budget=budget,
prices=prices,
media_scaler=media_scaler,
target_scaler=target_scaler,
seed=SEED)
Optimization terminated successfully (Exit mode 0)
Current function value: -1938.3914450904967
Iterations: 19
Function evaluations: 114
Gradient evaluations: 19得られた解に基づいて、最適予算配分を得ます。
# Obtain the optimal weekly allocation.
optimal_buget_allocation = prices * solution.x
optimal_buget_allocation
DeviceArray([174.72852, 285.152 , 132.38376, 128.85907, 276.38788], dtype=float32)
チェックとして、元の予算総額と最適化後の予算総額が等しくなるかどうかを見ます。
# Both values should be very close in order to compare KPI
budget, optimal_buget_allocation.sum()
(DeviceArray(997.5112, dtype=float32), DeviceArray(997.5112, dtype=float32))
# Both numbers should be almost equal
budget, jnp.sum(solution.x * prices)
(DeviceArray(997.5112, dtype=float32), DeviceArray(997.5112, dtype=float32))
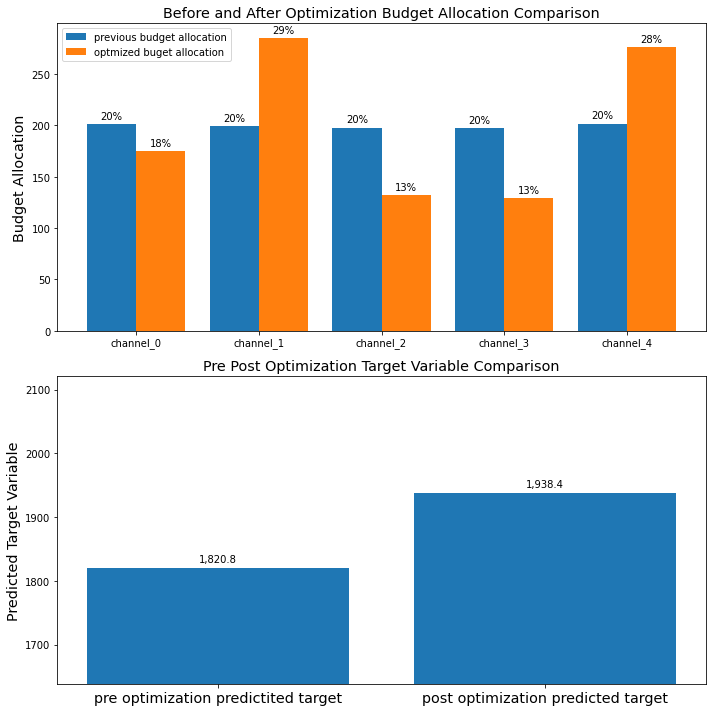
元の予算配分と、最適化後の予算配分とを、並べてプロットすることもできます。
# Plot out pre post optimization budget allocation and predicted target variable comparison. plot.plot_pre_post_budget_allocation_comparison(media_mix_model=mmm, kpi_with_optim=solution['fun'], kpi_without_optim=kpi_without_optim, optimal_buget_allocation=optimal_buget_allocation, previous_budget_allocation=previous_budget_allocation, figure_size=(10,10))
モデルの保存・読み込み
一応、推定したモデルの保存と読み込みもできるようになっています。Colabだと少しだけテクニックが必要です。
# We can use the utilities for saving models to disk. file_path = "media_mix_model.pkl" utils.save_model(media_mix_model=mmm, file_path=file_path)
# Once saved one can load the models. loaded_mmm = utils.load_model(file_path="media_mix_model.pkl") loaded_mmm.trace["coef_media"].shape # Example of accessing any of the model values.
コメントなど
個人的な感想を書いてしまうと、オリジナルとなったRStan実装よりもLMMMのNumPyro(だけでなくその他のパートも含めて)実装の方がソースコードが読みやすくて、「裏で何をしているか」「何をやろうとしてどういう実装がされているか」が非常に理解しやすいなと思ったのでした。それだけNumPyroが確率的プログラミング言語(PPL)として優れているということなのでしょう。僕もRStanにいつまでも固執していないで、NumPyroを本格的にやった方がいいのかなぁ、と……。
という脱線はさておき、実データでやる場合はこれよりもっと動作が重くなる可能性があるので、出来ればGPU環境で回すことをお薦めします(NumPyro自体がGPUモードを持っている)。RStanの時代からMMMというと計算が重たい統計モデリングの代表例だったわけですが、そこにもGPUによる高速化の恩恵がもたされることで、温故知新的な感じで改めてMMMが普及していくのかもしれない、という気がしています。
*1:間隔尺度なので正確には差分値でなければならない