一般に、データ分析の大半はそれほど高度なテクニックの類を必要としないものです。僕も常日頃から口に出して言うことが多いんですが、「統計学だの機械学習だのの出番なんてそもそも少なくて当たり前」。工数もかかるし、できればやらない方が良いです。ぶっちゃけ単純な四則演算で十分なケースの方が多数派でしょう。
なので、普段はDB上でSQL(というかHiveなど)でサクッと四則演算だけで集計処理を済ませてしまって、その結果だけを表示するようにしておいた方が圧倒的に楽で手っ取り早いはず。多くのBIツールもそういう考えのもとで作られていると思います。
ところがどっこい。世の中には、単純な四則演算での集計結果と、データサイエンスを駆使した分析結果とで、食い違ってしまうケースが何故かあることが知られています。どちらかと言うとレアケースだとは思いますが、その矛盾をおざなりにするととんでもないことになることも多々ありますので、今回はそのうちのごくごく一部について「どんな事例」で「どうして矛盾が起きるのか」を書いてみます。
(※続編があります→「なぜ項目ごとに単純な集計をするより、多変量解析(重回帰分析)をした方が正確な結果を返すのか」)
「組み合わせ」が強く影響しているケース
本編
GitHubにサンプルデータを上げておきました。手作りのサンプルデータなので結果が微妙かもですが*1、そこは予めご了承を。。。Rで演習しながら読み進めるという方は必要なRパッケージとして{randomForest}, {arules}, {arulesViz}*2をインストールして下さい。
イメージとしては、何かのECサイトでの行動ログ。a1からa7がユーザー行動の有無を0 or 1で記録したもので、cvがコンバージョンの有無(Yesなら有り・Noなら無し)。適当に作ったので、CVRはぴったり50%です。そこでCVの有無によってそれぞれのユーザー行動の有無のパーセンテージを集計してみると、
| a1 | a2 | a3 | a4 | a5 | a6 | a7 | CV |
|---|---|---|---|---|---|---|---|
| 40.1% | 58.3% | 47.9% | 94.2% | 30.7% | 5.6% | 50.0% | No |
| 60.5% | 41.7% | 49.4% | 43.6% | 68.4% | 92.7% | 49.3% | Yes |
という感じで、どの指標がCVRに効いているかが大体分かります。例えばa6はCV = "Yes"の側に寄せるのにものすごく貢献しているなぁとか、a4は逆にCV = "No"の側に寄せるのに強く貢献しているらしいとか。ごくごくわずかな差*3ではありますが、a7はCV = "No"の側に寄せるのに貢献していると言えそうですね。
ところで、この形のデータは普通に例えばGLMとか機械学習の諸手法とかにかけることができます。とりあえずRでGLMやってみましょう。CVの有無という二値データなので*4、family="binomial"で計算してみると
# サンプルデータは"sample_d"というデータフレームに入れてあるものとする > sample_d.glm<-glm(cv~.,sample_d,family="binomial") > summary(sample_d.glm) Call: glm(formula = cv ~ ., family = "binomial", data = sample_d) Deviance Residuals: Min 1Q Median 3Q Max -3.6404 -0.2242 -0.0358 0.2162 3.1418 Coefficients: Estimate Std. Error z value Pr(>|z|) (Intercept) -1.37793 0.25979 -5.304 1.13e-07 *** a1 1.05846 0.17344 6.103 1.04e-09 *** a2 -0.54914 0.16752 -3.278 0.00105 ** a3 0.12035 0.16803 0.716 0.47386 a4 -3.00110 0.21653 -13.860 < 2e-16 *** a5 1.53098 0.17349 8.824 < 2e-16 *** a6 5.33547 0.19191 27.802 < 2e-16 *** a7 0.07811 0.16725 0.467 0.64048 # ←コレだよコレ!!! --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 (Dispersion parameter for binomial family taken to be 1) Null deviance: 4158.9 on 2999 degrees of freedom Residual deviance: 1044.4 on 2992 degrees of freedom AIC: 1060.4 Number of Fisher Scoring iterations: 7
あれ?a7はクロス集計したパーセンテージだとCV = "No"に寄せるのに貢献しているはずなのに、GLMの結果はCV = "Yes"に寄せるのに貢献している「傾向」*5があるかも、という結果になってます。つまり、クロス集計しただけの結果とGLMの結果とが矛盾しているということです。有意な値ではないのでどうでもいいと言えばそれまでですが。。。
気になったので、一応Random Forestで変数重要度をチェックしてみます。
> tuneRF(sample_d[,-8],sample_d[,8],doBest=T) # 一応グリッドサーチでチューニング mtry = 2 OOB error = 6.67% Searching left ... mtry = 1 OOB error = 8.6% -0.29 0.05 Searching right ... mtry = 4 OOB error = 6.63% 0.005 0.05 Call: randomForest(x = x, y = y, mtry = res[which.min(res[, 2]), 1]) Type of random forest: classification Number of trees: 500 No. of variables tried at each split: 4 OOB estimate of error rate: 6.37% Confusion matrix: No Yes class.error No 1391 109 0.07266667 Yes 82 1418 0.05466667 > sample_d.rf<-randomForest(cv~.,sample_d,mtry=4) > importance(sample_d.rf) MeanDecreaseGini a1 18.593800 a2 10.052819 a3 6.983980 a4 189.841509 a5 52.050336 a6 956.140215 a7 8.536062 # ←コイツです
さすがにa7の変数重要度はそれほど大きくないですが、それでも最下位のa3よりはわずかながら大きいですね。もし、クライアントから「とにかくa1-a7の全てにそれぞれCVを増やすor減らす効果があるか教えてくれ」と言われたら、困ってしまうケースです*6。
何故こんなことが起きるんでしょうか? これを確かめるためにアソシエーション分析(バスケット分析)にかけてみました*7。その結果を{arulesViz}のグラフ構造プロットで可視化し、なおかつそのグラフ描画アルゴリズムを「類似しているものはより近いところに配置される」Fruchterman-Reingoldアルゴリズムに設定するとこうなります。

この図からはcv_yesもしくはcv_noからの距離に基づいてそれぞれのCVへの貢献度の強弱が見て取れます。これを上のGLM & Random Forestの結果と見比べると・・・そう、例えばa6がCV = "Yes"に強く貢献しているとかa4がCV = "No"に強く貢献しているというように一致している部分もあるんですが、問題は例のa7です。a7の位置はcv_yesに比較的近い位置、そしてa6にやや近い位置にあります。
実は、このサンプルデータを作る時に僕はあえてCV= "Yes"となるケースの一部に限ってa7をa6と強く相関するように細工しておきました。すなわち、データの中には「a6 & a7」という組み合わせがCV = "Yes"と強く関連するケースが一部ながら混じっていたというわけです。
それが「クロス集計したパーセンテージの大小で見るとa7はCV = "No"により強く貢献しているのに、データサイエンスの諸手法を用いると実はCV = "Yes"により強く貢献していることになる」という結果につながったんですねー。
というオチなんですが、これが実際のデータ分析の現場だったらかなり悩ましいシチュエーションですね。どうしても何かしらのレポートを出さなきゃいけないということであれば、僕なら「a7はa6との組み合わせにおいてのみCVR増に貢献していると考えられるので、a7はa6との間にどういう関係性があるのかをもっと細かく調べるべき」と答えることになると思います。ま、自分の仕事を増やすだけになりますが(笑)。
なお、今回のサンプルデータではサンプルサイズが3000と小さかったのでa7のような矛盾する結果を見せる変数の回帰係数がGLMでは有意になっていませんでしたが、もっとサンプルサイズが馬鹿でかい場合はa7のように矛盾する結果を見せる上にさらに統計学的に有意というデータサイエンス分析結果になることが全く珍しくないので、注意が必要です。
ツッコミをいただきました
裏先生から以下のごとく。
多変量解析では,他の変数も同時に影響を与えると考える訳であるから,逆に a7 と cv の「正味の相関関係」を知りたいならばどうするか。偏相関係数でしょう。
a1 a2 a3 a4 a5 a6 a7 a2 -0.027 a3 -0.005 0.003 a4 -0.005 0.012 0.019 a5 0.027 -0.007 -0.025 0.015 a6 -0.031 -0.013 0.018 -0.020 0.015 a7 0.006 -0.029 -0.031 0.007 -0.003 -0.011 cv 0.112 -0.059 0.003 -0.284 0.176 0.807 0.006
a1 ~ a6 の影響を取り除いた a7 と cv の偏相関係数は 0.006 ということです。
単相関係数は -0.007 と負の値であったけど,偏相関係数は正の値です。
ロジットモデルは重回帰分析とは違うけど,偏相関関係をあきらかにするという点では同じ。そもそも,ロジットモデルにしろ重回帰モデルにしろ,独立変数に掛けられる係数は「偏回帰係数」であって,それは偏相関係数の「偏」と同じ。つまり,他の変数の影響を取り除いて,その変数に掛ける重みということ。相関係数を評価するというのは,従属変数を独立変数1個で単回帰(直線回帰)するというのと同じ(数学的に等価)。
単純な分析で総合的な分析(多変量解析)の結果は予測できないということ。
「何故かある」のではなく,「必然的にある」。ごくたまに単純な分析結果から予想した結果が総合的な結果と一致することもあるのだが。
まことに仰る通りです*8。というか、何故ここで僕は真っ先に偏相関係数を考えなかったのか。これなら時間と手間のかかるアソシエーション分析やる必要全くないですね*9。学部1年生に戻ってやり直してきます。。。
ということで、自分の勉強のためにR上で手を動かしてみました。全部組んでもいいんですが、手間なので{ppcor}パッケージをインストールして使いました。
# sample_d$cvを0 or 1にas.numeric()などで変換しておく > pcor(sample_d2) $estimate a1 a2 a3 a4 a5 a1 1.000000000 -0.027097667 -0.004665751 -0.005058604 0.026653584 a2 -0.027097667 1.000000000 0.003302999 0.011735712 -0.007277052 a3 -0.004665751 0.003302999 1.000000000 0.019140545 -0.025398517 a4 -0.005058604 0.011735712 0.019140545 1.000000000 0.014636602 a5 0.026653584 -0.007277052 -0.025398517 0.014636602 1.000000000 a6 -0.030659270 -0.013304820 0.018187916 -0.020112145 0.015498244 a7 0.006356354 -0.028772727 -0.030596755 0.007394668 -0.002781801 cv 0.111647484 -0.058979223 0.002985735 -0.284084473 0.175562475 a6 a7 cv a1 -0.03065927 0.006356354 0.111647484 a2 -0.01330482 -0.028772727 -0.058979223 a3 0.01818792 -0.030596755 0.002985735 a4 -0.02011215 0.007394668 -0.284084473 a5 0.01549824 -0.002781801 0.175562475 a6 1.00000000 -0.010926019 0.807244783 a7 -0.01092602 1.000000000 0.005953911 cv 0.80724478 0.005953911 1.000000000 # ←ココがご指摘をいただいた箇所 $p.value a1 a2 a3 a4 a5 a1 0.000000e+00 0.138136964 0.79855664 7.820066e-01 1.447173e-01 a2 1.381370e-01 0.000000000 0.85662479 5.208875e-01 6.905865e-01 a3 7.985566e-01 0.856624786 0.00000000 2.950240e-01 1.646120e-01 a4 7.820066e-01 0.520887465 0.29502400 0.000000e+00 4.233077e-01 a5 1.447173e-01 0.690586496 0.16461200 4.233077e-01 0.000000e+00 a6 9.338115e-02 0.466719422 0.31972235 2.711839e-01 3.965254e-01 a7 7.280697e-01 0.115372742 0.09405176 6.858500e-01 8.790585e-01 cv 7.973833e-10 0.001230386 0.87026806 4.505601e-59 1.762439e-22 a6 a7 cv a1 0.09338115 0.72806975 7.973833e-10 a2 0.46671942 0.11537274 1.230386e-03 a3 0.31972235 0.09405176 8.702681e-01 a4 0.27118386 0.68584999 4.505601e-59 a5 0.39652541 0.87905852 1.762439e-22 a6 0.00000000 0.55005353 0.000000e+00 a7 0.55005353 0.00000000 7.446666e-01 cv 0.00000000 0.74466664 0.000000e+00 $statistic a1 a2 a3 a4 a5 a6 a1 0.0000000 -1.4827646 -0.2552155 -0.2767050 1.4584473 -1.6778256 a2 -1.4827646 0.0000000 0.1806723 0.6419780 -0.3980593 -0.7278271 a3 -0.2552155 0.1806723 0.0000000 1.0471639 -1.3897263 0.9950286 a4 -0.2767050 0.6419780 1.0471639 0.0000000 0.8006959 -1.1003404 a5 1.4584473 -0.3980593 -1.3897263 0.8006959 0.0000000 0.8478430 a6 -1.6778256 -0.7278271 0.9950286 -1.1003404 0.8478430 0.0000000 a7 0.3476943 -1.5744964 -1.6744013 0.4044933 -0.1521628 -0.5976799 cv 6.1454476 -3.2317408 0.1633180 -16.2069243 9.7546290 74.8125538 a7 cv a1 0.3476943 6.1454476 a2 -1.5744964 -3.2317408 a3 -1.6744013 0.1633180 a4 0.4044933 -16.2069243 a5 -0.1521628 9.7546290 a6 -0.5976799 74.8125538 a7 0.0000000 0.3256798 cv 0.3256798 0.0000000 $n [1] 3000 $gp [1] 6 $method [1] "pearson"
確かにa7とcvの偏相関係数は0.006で「正」の値になっていて、元の単相関係数の-0.007とは異なりCV = "Yes"に寄与しているということが分かりました。
ということで、ご指摘を受けて補足。多変量解析をやる時は偏相関係数にも注意(そして交互作用も)。裏先生、ご指摘ありがとうございました。
「率」を扱っているのに分母が変動しているケース
これは以前の記事(「カイゼンしたらコンバージョン率が○○%→△△%にup!」は分母を無視したら成り立たないかもしれない)でも取り上げた「CVRだけを計算しても意味があるかどうか」談義と同じケースですね。
つまり、ある課金を伴うゲームイベント(これをコンバージョンとする)の導線を改善したいと思って、従来の古いイベント導線に加えて新しく別のイベント導線を追加したとして、以下のような2×2の表を作って*10、
| 課金した | 課金しなかった | |
|---|---|---|
| 新イベント導線 | 5 | 2 |
| 旧イベント導線 | 150 | 140 |
さらにこれを以下のように解釈するとか。
| 課金した | 課金しなかった | 課金率 | |
|---|---|---|---|
| 新イベント導線 | 5 | 2 | 71% |
| 旧イベント導線 | 150 | 140 | 52% |
「新しいイベント導線の方が課金率71%!だから絶対新しいイベント導線の方が売上を伸ばせるから全面的に切り替えよう!」とか喜んでしまったら*11、いくら何でもまずいのでは?というお話ですね。
これまた以前の記事でも紹介しましたが、こういうケースでは独立性のカイ二乗検定orフィッシャーの正確確率検定を用いて*12、分母が違うことによる影響も加味した上でCVRに変化があったかどうかをチェックするのが筋でしょう。
> x=matrix(c(5,2,150,140),ncol=2,byrow=T) > print(x) [,1] [,2] [1,] 5 2 [2,] 150 140 > chisq.test(x) # 独立性のカイ二乗検定 Pearson's Chi-squared test with Yates' continuity correction data: x X-squared = 0.4205, df = 1, p-value = 0.5167 # 有意差なし:つまり両者に差はない 警告メッセージ: In chisq.test(x) : カイ自乗近似は不正確かもしれません # 「新イベント導線」のサンプルサイズが小さすぎると文句を言っている > fisher.test(x) # フィッシャーの正確確率検定:サンプルサイズの大小を問わず使えるが時間がかかることもある Fisher's Exact Test for Count Data data: x p-value = 0.4507 # やはり有意差なし:つまり両者に差はない alternative hypothesis: true odds ratio is not equal to 1 95 percent confidence interval: 0.3736408 24.8107839 sample estimates: odds ratio 2.326977
分母が大きく違っているにもかかわらず、ただ割り算だけして「○○率」を求めて、その値が大きかったor小さかったとかで何も考えずに一喜一憂していてはいけませんよ、ということで。
時系列データを扱うケース
意地の悪い例ですが、こんなケースを考えてみましょう。GitHubにサンプルデータその2を用意しておいたので、持ってきてRにx1とかいう名前で読み込ませて下さい。必要なRパッケージは{fGARCH}です。
さて、このデータなんですが。平均はどれくらいでしょうか? ちなみにこのデータのサンプルサイズは1200です。
> mean(x1) [1] 9989.522 > mean(x1[1:500]) [1] 9935.598 > mean(x1[501:1200]) [1] 10028.04 > mean(x1[701:900]) [1] 9934.387 > mean(x1[301:400]) [1] 9943.169
どこをどう切っても、大体10000ぐらいが平均値のようですね。じゃ、これは適当にばらついている平均10000ぐらいのデータなんだな。。。と思っていると大間違い。試しに分散を計算してみると、
> var(x1) [1] 1346957 > var(x1[1:500]) [1] 1489078 > var(x1[501:1200]) [1] 1243861 > var(x1[701:900]) [1] 252995.2 > var(x1[301:400]) [1] 3699340
あれ?切り出してきたところごとにまるっきり分散が違う?そこで、試しにこれを時系列でプロットしてやるとこうなります。

それもそのはず、このデータは実は
> x1<-rbind(matrix(rnorm(300,mean=10000,sd=200)),matrix(rnorm(300,mean=10000,sd=2000)), + matrix(rnorm(300,mean=10000,sd=500)),matrix(rnorm(300,mean=10000,sd=1000))) > plot.ts(x1)
と計算して得られたものだからです。つまり、平均は一定だけど分散(標準偏差)はタイムゾーンごとにてんでバラバラ。こうなっている時系列データをただ平均しただけでは何も分からなくて当然ですね~。ということで、時系列データの場合はただ平均を見るだけでなく、このようなばらつき(ボラティリティ:Volatility)も評価する必要があるケースがあるということを頭に入れておく必要があります。
こんなものは用心して毎回時系列プロット描くだけでも十分だと思いますが(笑)、どうしても細かく分析してみたいという場合は、例えば計量時系列分析のGARCH(一般化自己回帰条件付き分散不均一)モデルを推定することで、パラメータ推定や予測を行うことができます。
GARCHモデルとは何かというと、要は時系列データの生の値ではなく「分散の大きさ=(ばらつきorボラティリティ)」を改めて時系列データとして扱い、その挙動をモデリングするものです。これはどちらかというとあまりwebマーケには馴染みのない発想ですが、金融データのようにボラティリティ自体がリスク要因となる業界では大変重要な方法論です。
で、実際の計算は{fGARCH}パッケージを用いてこんな感じでやります*13。
> x1.garch<-garchFit(~garch(1,1),data=x1,trace=T) Series Initialization: ARMA Model: arma Formula Mean: ~ arma(0, 0) GARCH Model: garch Formula Variance: ~ garch(1, 1) ARMA Order: 0 0 Max ARMA Order: 0 GARCH Order: 1 1 Max GARCH Order: 1 Maximum Order: 1 Conditional Dist: norm h.start: 2 llh.start: 1 Length of Series: 1200 Recursion Init: mci Series Scale: 1160.585 Parameter Initialization: Initial Parameters: $params Limits of Transformations: $U, $V Which Parameters are Fixed? $includes Parameter Matrix: U V params includes mu -86.07318384 86.07318 8.607318 TRUE omega 0.00000100 100.00000 0.100000 TRUE alpha1 0.00000001 1.00000 0.100000 TRUE gamma1 -0.99999999 1.00000 0.100000 FALSE beta1 0.00000001 1.00000 0.800000 TRUE delta 0.00000000 2.00000 2.000000 FALSE skew 0.10000000 10.00000 1.000000 FALSE shape 1.00000000 10.00000 4.000000 FALSE Index List of Parameters to be Optimized: mu omega alpha1 beta1 1 2 3 5 Persistence: 0.9 --- START OF TRACE --- Selected Algorithm: nlminb R coded nlminb Solver: 0: 1454.2321: 8.60732 0.100000 0.100000 0.800000 1: 1339.3542: 8.56697 0.0446296 0.111299 0.779856 # 中略 47: 1146.4477: 8.61814 0.000875581 0.172139 0.849785 Final Estimate of the Negative LLH: LLH: 9614.463 norm LLH: 8.012052 mu omega alpha1 beta1 1.000208e+04 1.179370e+03 1.721390e-01 8.497848e-01 R-optimhess Difference Approximated Hessian Matrix: mu omega alpha1 beta1 mu -8.391052e-03 5.621736e-06 1.624651e-01 2.756090e-01 omega 5.621736e-06 -4.616137e-06 -1.335149e-01 -1.959011e-01 alpha1 1.624651e-01 -1.335149e-01 -1.819808e+04 -2.431246e+04 beta1 2.756090e-01 -1.959011e-01 -2.431246e+04 -3.595277e+04 attr(,"time") Time difference of 0.1320131 secs --- END OF TRACE --- Time to Estimate Parameters: Time difference of 0.7820778 secs > plot(x1.garch) Make a plot selection (or 0 to exit): 1: Time Series 2: Conditional SD 3: Series with 2 Conditional SD Superimposed 4: ACF of Observations 5: ACF of Squared Observations 6: Cross Correlation 7: Residuals 8: Conditional SDs 9: Standardized Residuals 10: ACF of Standardized Residuals 11: ACF of Squared Standardized Residuals 12: Cross Correlation between r^2 and r 13: QQ-Plot of Standardized Residuals Selection: 2 # 「分散の大きさ」の時系列データをプロットする > x1.pred<-predict(x1.garch,n.ahead=150,plot=T,nx=1200) # 150期先までの「分散の大きさ」を予測してプロットする
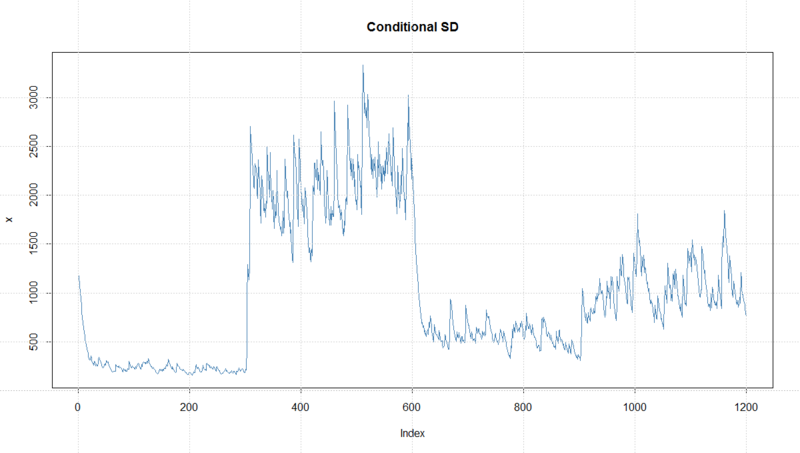

末広がりになってるのは、途中で分散がでかくなったからですね。ちなみにこれはものすごーーーく適当なサンプルデータなので、本来ならこんなGARCHモデルで扱うにはデタラメ過ぎます。参考までにgarchSim()関数で生成したもっと綺麗なシミュレーションデータに対するモデリングと予測の結果を載せておきましょう。
> set.seed(100) > x2<-garchSim(n=1200,garchSpec()) > plot(x2,lwd=2) > x2.garch<-garchFit(~garch(1,1),data=x2,trace=F) > plot(x2.garch) Make a plot selection (or 0 to exit): 1: Time Series 2: Conditional SD 3: Series with 2 Conditional SD Superimposed 4: ACF of Observations 5: ACF of Squared Observations 6: Cross Correlation 7: Residuals 8: Conditional SDs 9: Standardized Residuals 10: ACF of Standardized Residuals 11: ACF of Squared Standardized Residuals 12: Cross Correlation between r^2 and r 13: QQ-Plot of Standardized Residuals Selection: 2 > x2.pred<-predict(x2.garch,n.ahead=150,plot=T,nx=1200)


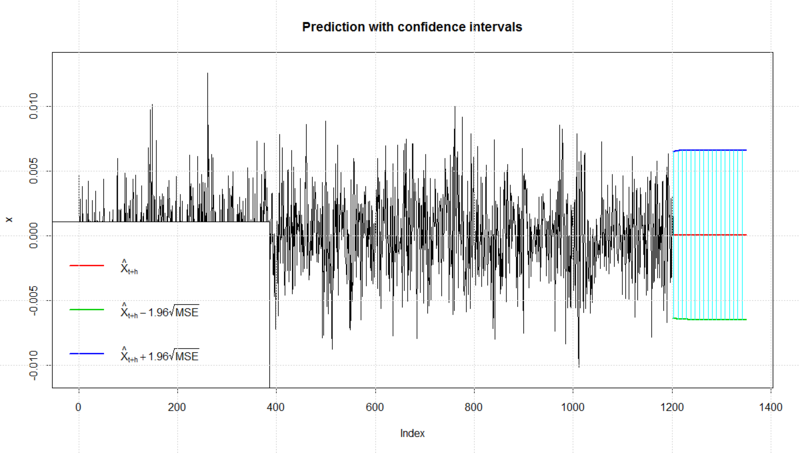
これは「分散の大きさ」*14が定常というシミュレートデータなので、その150期先予測も「分散の大きさ」が一定のまま、という結果になっています。
最後に
ということで、SQLで定期的に単純集計するBIツール組んで、定期的に数字orプロットを眺めて満足。。。していると危ないかもしれないので、適宜機械学習とか統計解析やってチェックしてみましょー、というお話でした(笑)。
ちなみにGARCHモデルは僕はノーマークなので、突っ込まれたら答えられません(泣)。一応沖本本7章に詳しい解説が載ってますが、詳しい人誰か教えてください。。。
余談
裏先生のツッコミをいただいてちょっと思い返したんですが、僕の場合実務で使わないものは一度勉強してもどんどん忘れていってしまうので、偏相関*15に限らず、例えば相関まわり全般、区間推定、そしてノンパラメトリック検定*16まわり、他にも確率過程や乱数理論あたりは多分相当怪しい気が。。。夏休みにちょっと集中して復習しようと思います。
*1:GLMに突っ込んだら標準回帰係数が5%有意じゃないとか
*2:glm()はデフォルトの{stats}に含まれるので何もしなくて大丈夫
*3:0.7%の差なんてないも同然ですがw
*4:Rでas.factor()を使って変換すると"No"の側に0, "Yes"の側に1が入る
*5:回帰係数が0より大きいため
*6:馬鹿にしちゃあいけません、そんなケースはデータ分析の現場に行けば腐るほどあります
*7:まずcvをcv_yes(CV = Yesの時に1 / それ以外は0)とcv_no(CV = Noの時に1 / それ以外は0)の2つのカラムに分け、この2カラムを残りのa1-a7の7カラムとくっつけて、マトリクスに変換すれば{arules}のapriori()関数に投げることができます
*8:ただし「何故か」と書いたのは単に読者の皆さんの注意を惹きたかっただけなので、「必然的ではない」という意味ではないのです
*9:ただし可視化できて分かりやすいという利点はありますが、統計学的には全くエレガントではない
*10:これは猛烈に極端な例です、念のため
*11:何度でも書きますがこれは猛烈に極端な例です、念のため
*12:chisq.test()もfisher.test()も{stats}に含まれるのでインストール不要
*13:GARCH(1,1)モデルを選択している理由については例えば沖本本p.156を参照のこと
*14:厳密には多分その対数だと思うんですが。。。
*15:確か4年前ぐらいに国際会議のプレゼン書く時に使った記憶がある
*16:順位和検定と符合つき順位和検定ぐらいしか思いつかない