渋谷駅前で働くデータサイエンティストのブログ

元祖「六本木で働くデータサイエンティスト」です / 道玄坂→銀座→東京→六本木→渋谷駅前

時系列モデリングのおさらい：季節調整とトレンド抽出

R BUGS/Stan MCMC 統計学 時系列分析

COVID-19が世界中に感染拡大し、日本含め多くの国で外出や集会の制限（自粛）措置が取られて久しい昨今ですが、これに伴って多くのところでCOVID-19に関連したオープンデータが公開されるようになっており、データ分析を生業とする人間が実データを扱う良い機会ともなっているように見受けられます。


ということで、今回の記事では東京都が公開している日次のCOVID-19感染者（PCR検査陽性者）報告数のデータを題材として、時系列モデリングのおさらいをしてみようと思います。なお、この記事における時系列モデリング結果は今後のCOVID-19の感染拡大状況について何かしらの解釈や予測をするためのものでは全くありません*1ので、悪しからずご了承ください。


また、この記事で公開しているコードは以前書いたクソコードをそのまま転用しているので、端的に言ってただのクソコードです。皆さん自身がお試しになる際は是非書き直すことをお薦めしますorz

Rのstl関数を用いて季節調整とトレンド抽出を行ってみる


Rにはstlというtsクラスを引数に取る簡単な時系列分析の関数があるので、これでさっくり季節調整とトレンド抽出をやってみましょう。これは以下のRコードを実行するだけです。


# Download the raw CSV file
d <- read.csv('https://stopcovid19.metro.tokyo.lg.jp/data/130001_tokyo_covid19_patients.csv')
# Extract date, with adding a dummy
d1 <- data.frame(day = d[, 5], num = 1)

# Aggregate as daily sum
library(dplyr)
d1$day <- as.Date(d1$day) # Put date into Date class
# Aggregate with group-by
d2 <- d1 %>% group_by(day) %>% summarise(sum(num)) %>% as.data.frame()
names(d2)[2] <- 'num'
# Set up a consecutive date vector
dayseq <- seq(from = as.Date(d2$day[1]), to = as.Date(d2$day[nrow(d2)]), by = 'day')
dayseq <- as.data.frame(dayseq)
names(dayseq) <- 'day'
# Join daily sum over the date vector
d3 <- left_join(dayseq, d2, by = 'day')
# Fill NAs by 0
d3[which(is.na(d3$num)), 2] <- 0

# Model trend and seasonality using stl (loess)
dts <- stl(ts(as.numeric(d3$num), frequency = 7), s.window = 'per')

# Create a title with start and end dates
mtitle <- paste0('Tokyo, daily from ', d3$day[1], ' to ', d3$day[nrow(d3)])

# Plot raw, trend and trend + seasonality time series
plot(d3$day, d3$num, main = mtitle,
     xlab = 'Date', ylab = 'Positive reported', type = 'l',
     ylim = c(-10, 230), col = 'black', lwd = 1)
par(new = T)
plot(d3$day, dts$time.series[, 2], main = mtitle,
     xlab = 'Date', ylab = 'Positive reported', type = 'l',
     ylim = c(-10, 230), col = 'blue', lwd = 3)
par(new = T)
plot(d3$day, dts$time.series[, 2] + dts$time.series[, 1],
     main = mtitle, xlab = 'Date', ylab = 'Positive reported',
     type = 'l', col = 'red', ylim = c(-10, 230), lty = 2)
legend('topleft', legend = c('Reported', 'Trend', 'Trend + Seasonality'),
       col = c('black', 'blue', 'red'), lty = c(1, 1, 3),
       lwd = c(1, 3, 2), ncol = 1)

f:id:TJO:20200429150940p:plain

4月29日15時時点で公開されているデータを用いた限りではこんな感じになります。ただ、stlではLOESSを使って「周期成分の振幅は一定」という仮定のもとで季節調整を行っているため、周期成分が絶対値の小さな初期フェーズであっても算入されてしまっていて少しおかしなことになってしまっています。


RStanで一階差分トレンドモデルを推定してみる


そこで、一足飛びに今度はRStanで一階差分トレンド*2モデルの推定をやってみます。これも以下のStanコードとRコードを用意して、ただ回すだけです。



data {
  int<lower=0> N;
  real<lower=0> y[N];
}

parameters {
  real season[N];
  real trend[N];
  real s_trend;
  real s_season;
  real s_q;
}

model {
  real q[N];
  for (i in 7:N)
    season[i] ~ normal(-season[i - 1] - season[i - 2] - season[i - 3] - season[i - 4] - season[i - 5] - season[i - 6], s_season);	
  for (i in 2:N)
    trend[i] ~ normal(trend[i - 1], s_trend);
  for (i in 1:N)
    q[i] = y[i] - season[i] - trend[i];
  for (i in 1:N)
    q[i] ~ normal(0, s_q);
}

# Download the raw CSV file
d <- read.csv('https://stopcovid19.metro.tokyo.lg.jp/data/130001_tokyo_covid19_patients.csv')
# Extract date, with adding a dummy
d1 <- data.frame(day = d[, 5], num = 1)

# Aggregate as daily sum
library(dplyr)
d1$day <- as.Date(d1$day) # Put date into Date class
# Aggregate with group-by
d2 <- d1 %>% group_by(day) %>% summarise(sum(num)) %>% as.data.frame()
names(d2)[2] <- 'num'
# Set up a consecutive date vector
dayseq <- seq(from = as.Date(d2$day[1]), to = as.Date(d2$day[nrow(d2)]), by = 'day')
dayseq <- as.data.frame(dayseq)
names(dayseq) <- 'day'
# Join daily sum over the date vector
d3 <- left_join(dayseq, d2, by = 'day')
# Fill NAs by 0
d3[which(is.na(d3$num)), 2] <- 0

# Set up Stan env
library(rstan)
options(mc.cores = parallel::detectCores())
rstan_options(auto_write = TRUE)

# Data as a list
N <- nrow(d3)
y <- d3$num
dat <- list(N = N, y = y)

# Fit by Stan
fit <- stan('covid19_tokyo_local_trend.stan', data = dat,
            iter = 1000, chains = 4)

# Extract MCMC samples to obtain MLE parameters
fit.smp<-extract(fit)
trend <- rep(0, N)
for (i in 1:N) {
  tmp <- density(fit.smp$trend[, i])
  trend[i] <- tmp$x[tmp$y == max(tmp$y)]
}
season <- rep(0, N)
for (i in 1:N) {
  tmp <- density(fit.smp$season[, i])
  season[i] <- tmp$x[tmp$y == max(tmp$y)]
}
# Fitted time series
pred <- trend + season

# Create a title with start and end dates
mtitle <- paste0('Tokyo, daily from ', d3$day[1], ' to ', d3$day[nrow(d3)])

# Plot
matplot(cbind(y, pred, trend),
        type = 'l', lty = c(1, 3, 1), lwd = c(1, 2, 3), col = c(1, 2, 4),
        ylab = '', main = mtitle)
legend('topleft', legend = c('Reported', 'Local trend + seasonality', 'Local Trend'),
       lty = c(1, 3, 1), lwd = c(1, 2, 3), col = c(1, 2, 4))

f:id:TJO:20200429151534p:plain

季節調整の振幅が時変になり、トレンドの抽出も出来ていますが、ちょっとトレンドがギザギザして推定されてしまっているようです。


RStanで二階差分トレンドモデルを推定してみる


そこで、ダメ押しでRStanで二階差分トレンドモデルを推定してみます。これはStanコードを見れば分かりますが「傾きの『変化量』が確率的にばらつく」という仮定を置くもので、一階差分トレンドよりもさらに滑らかに変化するトレンドを推定するものです。



data {
  int<lower=0> N;
  real<lower=0> y[N];
}

parameters {
  real season[N];
  real trend[N];
  real s_trend;
  real s_season;
  real s_q;
}

model {
  real q[N];
  real cum_trend[N];
  for (i in 7:N)
    season[i] ~ normal(-season[i - 1] - season[i - 2] - season[i - 3] - season[i - 4] - season[i - 5] - season[i - 6], s_season);	
  for (i in 3:N)
    trend[i] ~ normal(2 * trend[i - 1] - trend[i - 2], s_trend);
  
  cum_trend[1] = trend[1];
  for (i in 2:N)
    cum_trend[i] = cum_trend[i - 1] + trend[i];
  for (i in 1:N)
    q[i] = y[i] - season[i] - cum_trend[i];
  for (i in 1:N)
    q[i] ~ normal(0, s_q);
}

# Download the raw CSV file
d <- read.csv('https://stopcovid19.metro.tokyo.lg.jp/data/130001_tokyo_covid19_patients.csv')
# Extract date, with adding a dummy
d1 <- data.frame(day = d[, 5], num = 1)

# Aggregate as daily sum
library(dplyr)
d1$day <- as.Date(d1$day) # Put date into Date class
# Aggregate with group-by
d2 <- d1 %>% group_by(day) %>% summarise(sum(num)) %>% as.data.frame()
names(d2)[2] <- 'num'
# Set up a consecutive date vector
dayseq <- seq(from = as.Date(d2$day[1]), to = as.Date(d2$day[nrow(d2)]), by = 'day')
dayseq <- as.data.frame(dayseq)
names(dayseq) <- 'day'
# Join daily sum over the date vector
d3 <- left_join(dayseq, d2, by = 'day')
# Fill NAs by 0
d3[which(is.na(d3$num)), 2] <- 0

# Set up Stan env
library(rstan)
options(mc.cores = parallel::detectCores())
rstan_options(auto_write = TRUE)

# Data as a list
N <- nrow(d3)
y <- d3$num
dat <- list(N = N, y = y)

# Fit by Stan
fit <- stan('covid19_tokyo_2nd_trend.stan', data = dat,
            iter = 1000, chains = 4)

# Extract MCMC samples to obtain MLE parameters
fit.smp<-extract(fit)
trend <- rep(0, N)
for (i in 1:N) {
  tmp <- density(fit.smp$trend[, i])
  trend[i] <- tmp$x[tmp$y == max(tmp$y)]
}
season <- rep(0, N)
for (i in 1:N) {
  tmp <- density(fit.smp$season[, i])
  season[i] <- tmp$x[tmp$y == max(tmp$y)]
}
# Fitted time series
pred <- cumsum(trend) + season

# Create a title with start and end dates
mtitle <- paste0('Tokyo, daily from ', d3$day[1], ' to ', d3$day[nrow(d3)])

# Plot
matplot(cbind(y, pred, cumsum(trend)),
        type = 'l', lty = c(1, 3, 1), lwd = c(1, 2, 3), col = c(1, 2, 4),
        ylab = '', main = mtitle)
legend('topleft',
       legend = c('Reported', '2nd-diff Trend + Seasonality', '2nd-diff Trend'),
       lty = c(1, 3, 1), lwd = c(1, 2, 3), col = c(1, 2, 4))

f:id:TJO:20200429152157p:plain

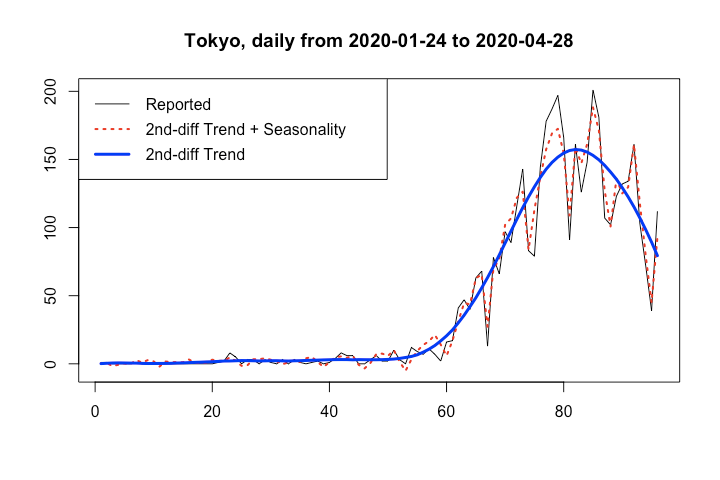
もう少しトレンドが綺麗で滑らかになり、同時に周期成分も振幅が時変になって初期フェーズで暴れることもなくなり、それっぽい当てはめ結果になりました。

*1:それらはauthorizeされた専門家の方々のお仕事です

*2:用語の混乱を避けるためにトレンド定義式に沿った呼称に改めました。経緯はコメント欄参照のこと