これはただの備忘録です。目新しい内容は特に何もありません。きちんとした内容を学びたいという方は、先日著者の萩原さんからご恵贈いただいたこちらの書籍で学ばれることをお薦めいたします。MCMCに留まらず、粒子フィルタの実装&実践までカバーしていて素晴らしい教科書だと思います。

基礎からわかる時系列分析 ―Rで実践するカルマンフィルタ・MCMC・粒子フィルター (Data Science Library)
- 作者: 萩原淳一郎,瓜生真也,牧山幸史,石田基広
- 出版社/メーカー: 技術評論社
- 発売日: 2018/03/23
- メディア: 大型本
- この商品を含むブログ (1件) を見る
で、今回取り上げるのは時変係数から成る動的線形モデルです。マーケティング分析では割と時不変係数モデルが暗黙のうちに採用されることが多いのですが、一方で「おいこれどう見ても特定の特徴量の係数は時変やろ」みたいなケースも時々見かけることがあってやろうとは思っていたものの、単にStanでどう書くか考えるのが面倒で放っていたという(笑)。ということで、今回は真面目にやってみようと思います。
シミュレーションデータを作る
適当に乱数シードを選んで作っておきます。ただし時変係数のところとかはシードをきちんと指定できないので同じようにはいかないと思いますので、皆さんのお手元で適宜調整してください。
> set.seed(1001) > x1 <- runif(100, 3, 5) > set.seed(1002) > x2 <- runif(100, 4, 7) > set.seed(1003) > x3 <- runif(100, 8, 15) > sd1 <- 0.1 > sd2 <- 0.2 > sd3 <- 0.05 > sd_y <- 5 > b1 <- rep(0, 100) > b1[1] <- 2 > for (i in 2:100){ + b1[i] <- b1[i-1] + rnorm(1, 0, sd1) + } > b2 <- rep(0, 100) > b2[1] <- 3 > for (i in 2:100){ + b2[i] <- b2[i-1] + rnorm(1, 0, sd2) + } > b3 <- rep(0, 100) > b3[1] <- 0.5 > for (i in 2:100){ + b3[i] <- b3[i-1] + rnorm(1, 0, sd3) + } > b0 <- 10 > y <- rep(0, 100) > for (i in 1:100){ + y[i] <- b0 + b1[i] * x1[i] + b2[i] * x2[i] + b3[i] * x3[i] + } > y <- y + rnorm(100, 0, sd_y)
見ての通りで、基本的には3説明変数と1バイアスから成る動的線形モデルです。ただし個々の説明変数にかかる係数は単位根過程(=ローカル線形トレンド)に従う時変パラメータです。目的変数をプロットするとこうなります。
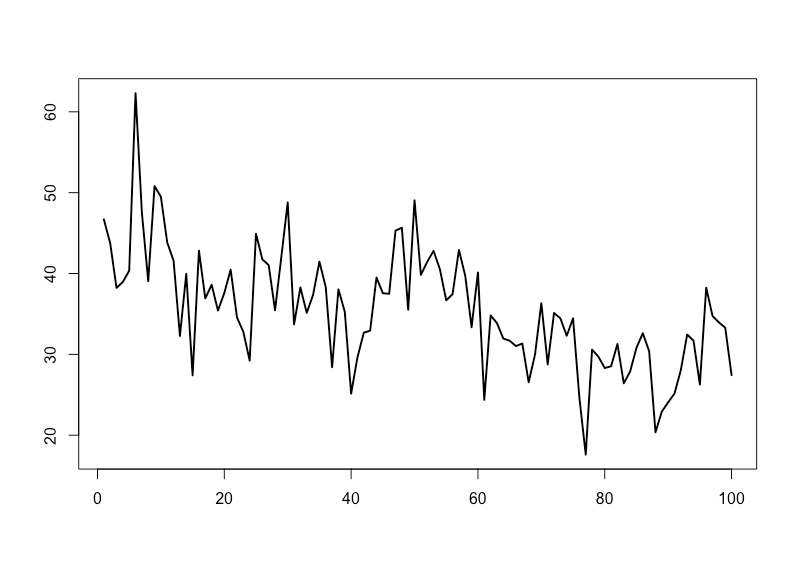
何かどう見てもローカル線形トレンドか二回差分トレンドのありそうなデータになってしまいましたが、一旦これで良しとします。
Stanで推定する
あとはベタッとStanで書くだけです。本来ならきちんと個々のサンプル間の関係をDAGにして数式で書いておくべきなんでしょうが、ただの備忘録なのでここでは割愛します。Stanコードは以下の通り。例えば"dlm_tv.stan"みたいな名前で保存しておきます。
data {
int<lower=0> N;
int<lower=0> M;
matrix[N, M] X;
real<lower=0> y[N];
}
parameters {
real s_q;
vector<lower=0>[M] s_b;
matrix<lower=0>[N, M] beta;
real d_int;
}
model {
for (i in 2:N){
for (j in 1:M){
beta[i, j] ~ normal(beta[i-1, j], s_b[j]);
}
}
for (i in 1:N)
y[i]~normal(dot_product(X[i,], beta[i,]) + d_int, s_q);
}
これを以下のRコードでkickします。
> mx <- cbind(x1, x2, x3) > dat <- list(N = nrow(mx), M = ncol(mx), y = y, X = mx) > library(rstan) > options(mc.cores = parallel::detectCores()) > rstan_options(auto_write = TRUE) > fit <- stan(file = 'dlm_tv.stan', data = dat, iter = 1000, chains = 4) ## 中略 ## > slength <- 2000 > fit.smp <- extract(fit) > tmp <- density(fit.smp$d_int) > d_int <- tmp$x[tmp$y == max(tmp$y)] > tmp <- density(fit.smp$s_q) > s_q <- tmp$x[tmp$y == max(tmp$y)] > s_beta <- rep(0, ncol(mx)) > for (i in 1:ncol(mx)) { # tmp <- density(fit.smp$beta[(slength*(i-1)+1):(slength*i)]) + tmp <- density(fit.smp$s_b[(slength*(i-1)+1):(slength*i)]) # 萩原さんからバグをご指摘いただいたのでこちらに修正 + s_beta[i] <- tmp$x[tmp$y == max(tmp$y)] + } > tmp <- fit.smp$beta > beta <- matrix(0, nrow = nrow(mx), ncol = ncol(mx)) > for (i in 1:nrow(mx)){ + for (j in 1:ncol(mx)){ + tmpb <- density(tmp[, i, j]) + beta[i, j] <- tmpb$x[tmpb$y == max(tmpb$y)] + } + } > y_pred <- rep(0, 100) > for (i in 1:100){ + y_pred[i] <- d_int + beta[i, 1] * x1[i] + beta[i, 2] * x2[i] + beta[i, 3] * x3[i] + } > matplot(cbind(y, y_pred), type = 'l', xlab = '', ylab = '', lwd = 2) > legend('topright', legend = c('Data', 'Fitted'), col = c(1,2), lty = c(1,2), lwd = 2)

見た感じフィッティング感は悪くないようです。では時変係数のフィッティングを見てみましょう。
> par(mfrow = c(3, 1)) > matplot(cbind(b1, beta[, 1]), type = 'l', xlab = '', ylab = '', lwd = 2, main = 'Beta 1') > matplot(cbind(b2, beta[, 2]), type = 'l', xlab = '', ylab = '', lwd = 2, main = 'Beta 2') > matplot(cbind(b3, beta[, 3]), type = 'l', xlab = '', ylab = '', lwd = 2, main = 'Beta 3')
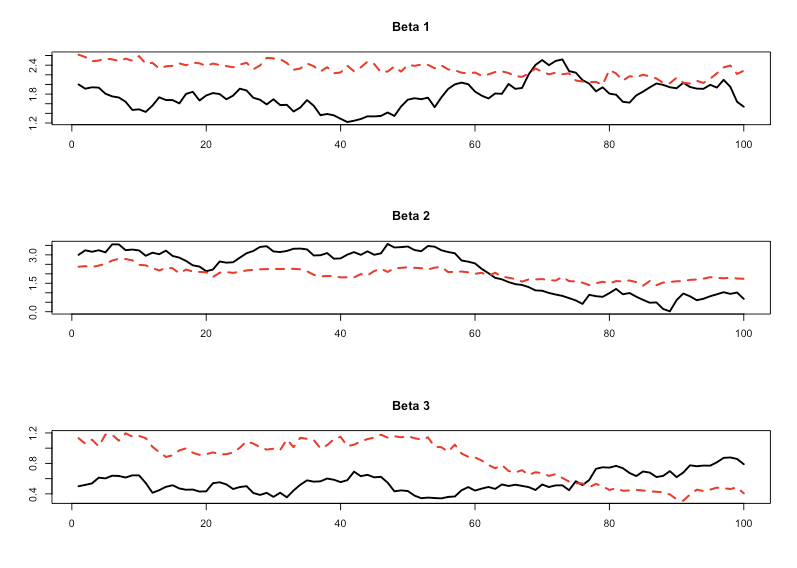
これ全然合ってない気がしますねorz まぁ"All models are wrong, but some are useful"ということで時変係数モデルのようなフリーパラメータの多いモデルだとこういうこともあるのかなと。最後にMCMCサンプリングの収束具合を見ておきます。
> options(max.print = 10000) > fit Inference for Stan model: dlm_tv. 4 chains, each with iter=1000; warmup=500; thin=1; post-warmup draws per chain=500, total post-warmup draws=2000. mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat s_q 4.22 0.02 0.41 3.49 3.93 4.21 4.50 5.08 360 1.01 s_b[1] 0.18 0.03 0.12 0.02 0.08 0.16 0.25 0.46 18 1.23 s_b[2] 0.14 0.03 0.09 0.02 0.07 0.13 0.20 0.35 7 1.30 s_b[3] 0.08 0.01 0.04 0.02 0.06 0.08 0.11 0.16 30 1.09 beta[1,1] 2.90 0.16 1.04 1.13 2.16 2.82 3.53 5.22 40 1.06 beta[1,2] 2.48 0.09 0.85 0.82 1.90 2.46 3.06 4.09 84 1.05 beta[1,3] 1.09 0.03 0.38 0.42 0.82 1.08 1.35 1.85 135 1.03 beta[2,1] 2.89 0.17 1.04 1.13 2.14 2.80 3.49 5.23 38 1.06 beta[2,2] 2.46 0.09 0.83 0.83 1.91 2.44 3.03 4.05 86 1.05 beta[2,3] 1.08 0.03 0.37 0.43 0.81 1.07 1.32 1.82 129 1.02 ## 中略 ## beta[99,1] 2.44 0.06 0.89 0.89 1.81 2.37 3.00 4.41 251 1.00 beta[99,2] 1.82 0.06 0.69 0.53 1.36 1.80 2.29 3.21 135 1.02 beta[99,3] 0.56 0.02 0.29 0.10 0.34 0.53 0.76 1.17 151 1.01 beta[100,1] 2.42 0.06 0.92 0.82 1.76 2.36 3.00 4.47 244 1.00 beta[100,2] 1.80 0.06 0.70 0.46 1.32 1.78 2.29 3.24 135 1.02 beta[100,3] 0.56 0.02 0.29 0.09 0.34 0.53 0.75 1.17 144 1.01 d_int 4.29 0.45 4.86 -5.73 1.07 4.49 7.64 13.44 115 1.02 lp__ 442.13 18.16 84.74 308.06 379.70 430.10 496.34 631.20 22 1.11 Samples were drawn using NUTS(diag_e) at Sat May 19 15:16:18 2018. For each parameter, n_eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence, Rhat=1).
Rhatは大体1.00に近いあたりをどのパラメータでも推移していてそこまで悪くはなさそうです。最後に{coda}でMCMCサンプルのヒストグラムを見てみましょう。
> library(coda) > fit.coda<-mcmc.list(lapply(1:ncol(fit),function(x) mcmc(as.array(fit)[,x,]))) > plot(fit.coda[,5:7]) > plot(fit.coda[,302:304]) > plot(fit.coda[,305:306])
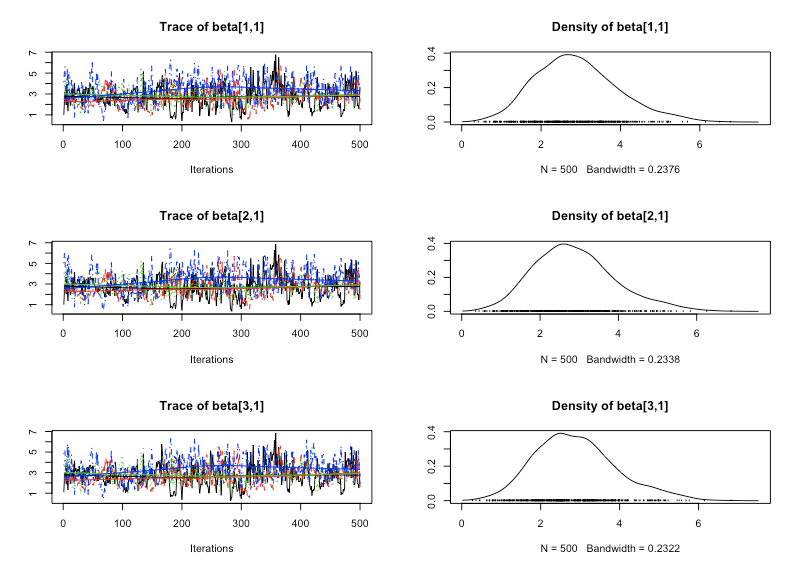
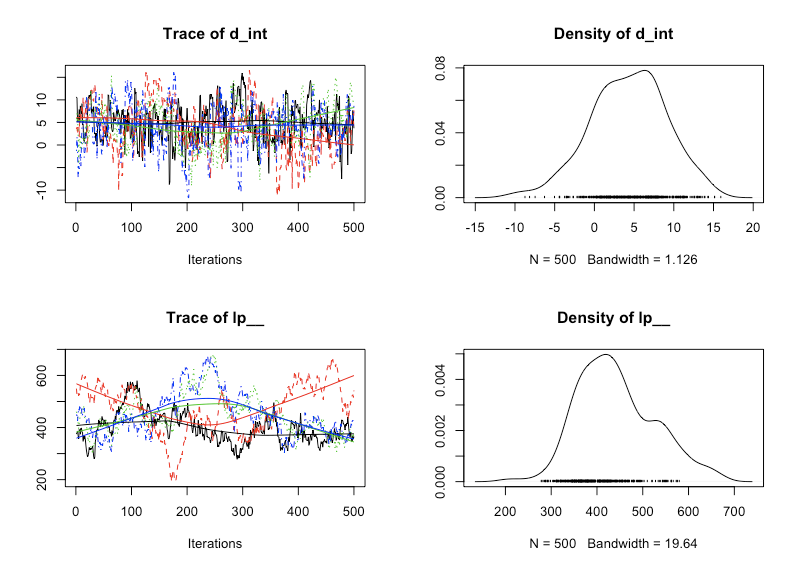
ヒストグラムを見た感じもそこまで収束具合は悪くなさそうです。とりあえず、今回のやり方で一応時変係数動的線形モデルの推定がStanで出来るということは分かりました。後はきちんとこれが適用できて尚且つフィッティングも良くてさらに汎化性能も確保できるようなやり方と、データの組み合わせを探す感じですかね。。。
追記
『基礎からわかる時系列分析』の著者、萩原さんから以下のように{dlm}パッケージを使った場合のフォローアップ記事を頂戴しました。萩原さん、有難うございます。この程度の計算なら&特に事後分布が欲しいわけではないのであれば、{dlm}パッケージを使った方が圧倒的に速いです(試してみてやっぱりなぁ…となりました)。
また上のRコード内のバグもご指摘いただきましたので、1点修正してあります。大変失礼いたしましたm(_ _)m
ところで萩原さんからは、
この結果を見ると、モデルのパラメータを真値に設定すると状態(平均値)の推定精度は若干向上するものの、限界はある印象を受けます。 従って、回帰係数の推定精度を追求する観点では、今回のデータは元々やや手ごわいものになっているのではないかと感じます。
という感想を頂戴しているのですが、後になって見返してみたら「そりゃそうだよな」と思ってしまいました。理由は簡単で、3つの真の時変係数同士を比べてみると
> matplot(scale(cbind(b1, b2, b3)), type = 'l', lty = 1, ylab = '') > cor(cbind(b1,b2,b3)) b1 b2 b3 b1 1.0000000 -0.6065728 -0.4004846 b2 -0.6065728 1.0000000 0.8616015 b3 -0.4004846 0.8616015 1.0000000
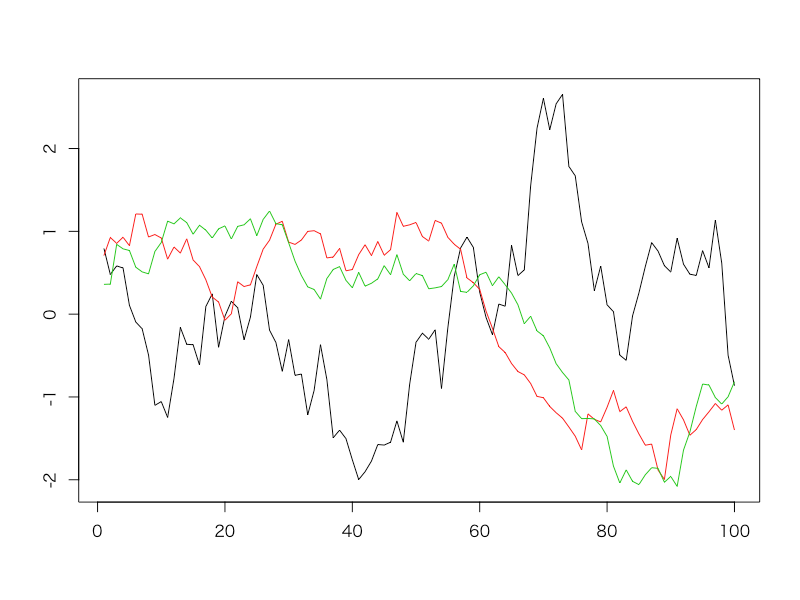
見ての通りb2とb3とで相関が高く、多重共線性が高くなるのと同様の現象を起こしていたからですorz もうちょっと適切なシミュレーションデータを作るべきだったと反省しております。。。