今年の1月にこんな話題を取り上げたわけですが。
この記事の最後にちょろっと書いた通り、実際にはこういう"too good to be true"即ち「そのモデルの精度いくら何でも高過ぎるんじゃないの?」→「実は汎化性能見てませんでした」みたいなケースって、想像よりも遥かに多くこの世の中存在するみたいなんですね。ということで、それこそ『はじパタ』の2章とかPRMLの最初の方に出てくる初歩中の初歩なんですが、その辺の話を改めてだらだら書いてみようと思います。
そもそも「精度100%」とか「相関係数0.9以上」とか見たら身構えるべき
冒頭に挙げた例は、そもそも「精度100%なんておかしい」という声があちこちから挙がったことで話題になり、蓋を開けてみたらleakageはあるわ訓練誤差でしか評価してないわで散々だったわけです。
一般に、実世界のデータセットで統計モデリングにせよ機械学習にせよモデリングする場合、計測の誤差やノイズが存在することを考えれば、精度100%になるなんてことはまずあり得ません。同様に相関係数が0.9以上というのも、正直言って実世界のデータセットを相手にする限りはほとんど聞かれない数字だと思います。
そのような"too good to be true"なモデル精度の話題が出てきたら、まず真っ先に「何かおかしいのではないか?」と疑ってかかる癖をつけた方が良いと個人的には思ってます。その上で、以下のようなポイントを精査すべきなのかなと。
過学習・汎化性能とは
かの『はじパタ』でもPRMLでも最初の方に出てくる超絶有名な話なんですが、一応おさらいしておきましょう。全く同じものでやるのは面白くないので、面倒ですが自分で似たものを用意しました*1。
まず、以下のようなデータセットを想定します。ただし、実際には全部で21点のあるルールに従って生成したデータのうち16点のみをプロットしてあります。この16点を「学習データ」とし、残りの5点を「テストデータ」とします。
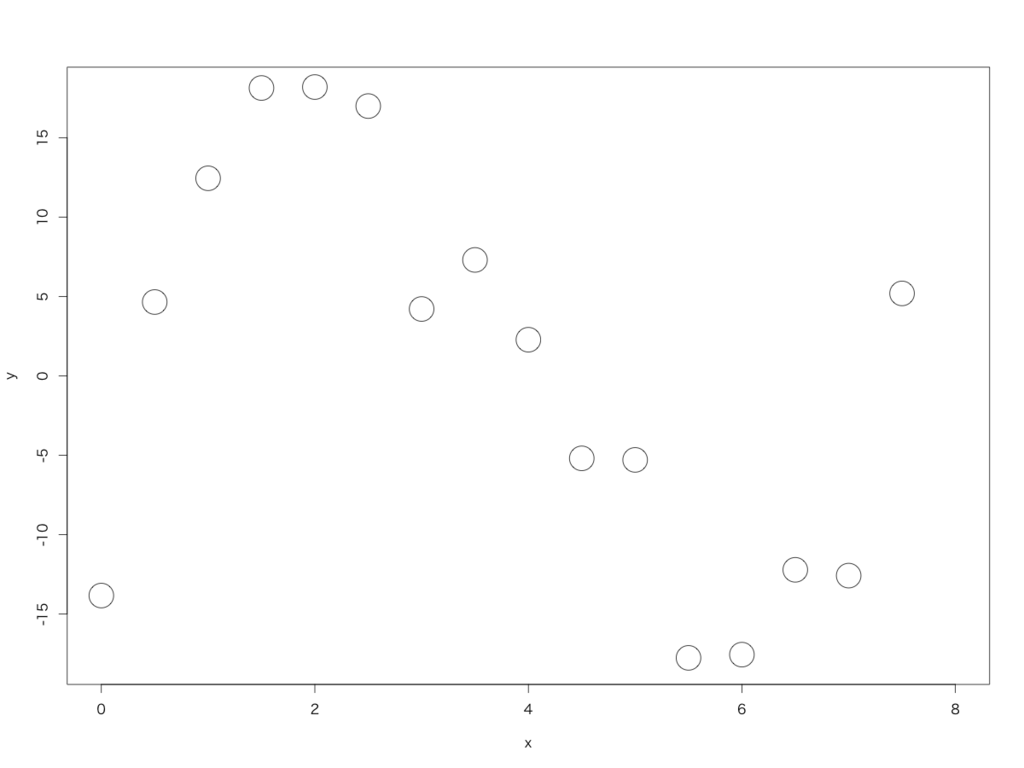
見た感じS字カーブっぽいので、例えば3次の多項式で近似(学習)してみましょう。すると、以下のような感じになります。

でも、ちょっと精度としてはちょっと物足りない気がするので、次数を上げて9次の多項式で近似してみましょう。結果は以下の青線の通り。

ちなみにこの2つの近似結果と元の16点のデータとの相関係数を計算してみると、3次の多項式では0.968、9次の多項式では0.986という結果になり、9次の多項式で近似した方がこの16点に対する当てはめ精度は高いということになります。
なのですが。本当にこれで良いのでしょうか? 実は、全部で21点あるデータを全てプロットすると、以下のようになります。
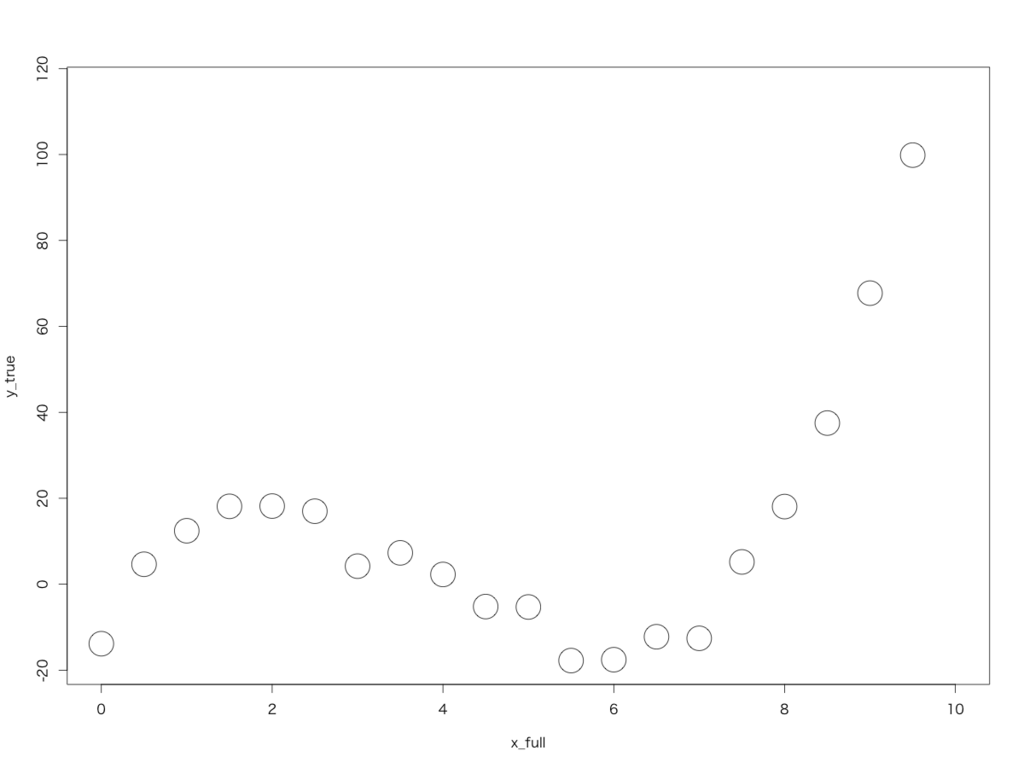
これに、先ほどの3次の多項式で近似(学習)したモデルによる予測曲線と、9次の多項式で近似したモデルによる予測曲線を重ね描きしてみると、こうなります。

もうお分かりでしょう。3次多項式モデルは残りの5点に対してもほぼフィットしているのに対して、9次多項式モデルは途中からあさっての方向に吹っ飛んでしまっています。
この元の21点のデータはという3次関数に正規分布するノイズを加えて生成したものなので、当たり前ですが3次の多項式で近似した方が「学習データには存在しなかった」残り5点のテストデータに対する予測精度は良くなります。つまり、ベストのモデルは3次多項式モデルであり、9次多項式モデルは良くないモデルだということになるわけです。
『はじパタ』やPRMLでも述べられているように、こういう時に9次多項式モデルのような事態に陥ることを「過学習」(overfitting)と呼びます。一方で3次多項式モデルのように「学習モデルへの当てはまりは必ずしも良くないものの未知データ(テストデータ)への当てはまりが良い」ことを「汎化性能(汎化能力:generalization)」と呼びます。
この例からも分かるように、基本的には適切な学習モデルを選択したい場合は「できるだけ過学習しておらず汎化性能に優れた」モデルを優先すべき、だと言えます。言い換えると、観測されたデータを生成している(データの背後にある)真のモデルに近付くためには、未知データ(テストデータ)にもきちんと当てはまる汎化性能に優れたモデルを採用するべき、とも言えると思います。
「予測」より「説明」を重視するが故の落とし穴
ところが、学習データのみに対する精度だけを見てモデルの評価をしてしまうケースは、世の中少なからずあるようです。その理由として、学習したモデルの予測性能を重視するのではなく、そのモデルのパラメータ(偏回帰係数)の大小だけに(も)興味があるケースでは、むしろ学習データに対する精度(もしくは訓練誤差)のみを拠り所にしてしまうことがあるとかないとか。
冒頭に挙げた例でも、予測性能もさることながらその回帰式(説明変数×偏回帰係数のラインナップ)自体にも意味を持たせたかったようで、それで訓練誤差しか見ないという結果につながっていたように見受けられます。
しかしながら、仮にモデルのパラメータ(偏回帰係数)の大小にしか興味がないケースであっても、汎化性能に劣る過学習したモデルを採用することには大いに問題があると思われます。実際、先ほどの3次関数生成データに対する3次多項式モデルvs.9次多項式モデルによる近似結果を、普通の線形回帰モデル(最小二乗法)に基づいて推定したパラメータとともに例示すると以下のようになります。
> summary(lm3) Call: lm(formula = y ~ V1 + V2 + V3, data = d) Residuals: Min 1Q Median 3Q Max -7.8075 -1.6179 0.7592 1.8565 5.8518 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -12.10054 2.86446 -4.224 0.00118 ** V1 35.24213 3.41855 10.309 2.58e-07 *** V2 -12.15388 1.08009 -11.253 9.87e-08 *** V3 1.02871 0.09454 10.882 1.43e-07 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 3.559 on 12 degrees of freedom Multiple R-squared: 0.9368, Adjusted R-squared: 0.921 F-statistic: 59.28 on 3 and 12 DF, p-value: 1.819e-07 > summary(lm9) Call: lm(formula = y ~ ., data = d) Residuals: Min 1Q Median 3Q Max -3.7139 -0.7857 -0.2104 0.8271 4.1045 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -1.389e+01 3.287e+00 -4.226 0.00553 ** V1 9.606e+01 4.339e+01 2.214 0.06879 . V2 -2.145e+02 1.358e+02 -1.579 0.16530 V3 2.729e+02 1.694e+02 1.611 0.15836 V4 -1.871e+02 1.093e+02 -1.712 0.13773 V5 7.276e+01 4.047e+01 1.798 0.12229 V6 -1.664e+01 8.938e+00 -1.861 0.11199 V7 2.216e+00 1.163e+00 1.906 0.10529 V8 -1.591e-01 8.216e-02 -1.936 0.10099 V9 4.755e-03 2.431e-03 1.956 0.09829 . --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 3.289 on 6 degrees of freedom Multiple R-squared: 0.973, Adjusted R-squared: 0.9325 F-statistic: 24.03 on 9 and 6 DF, p-value: 0.0004908
言うまでもなく、lm3(3次多項式モデル)はほぼ正確に元の3次関数に近いパラメータ推定結果を返しているのに対して、lm9(9次多項式モデル)はほとんどデタラメに近い結果を返しています。つまり、過学習しているモデルはそもそもパラメータ推定という意味でも役に立たないというわけです。
いわゆるwebマーケティングの世界だとこの手の重回帰分析のパラメータ推定結果に基づいて例えば「もっと○○施策に注力すべき」「もっと△△にコストをかけるべき」みたいな意思決定をすることもあるわけですが、もし過学習したモデルでそんなことをした日には最悪の事態になることもあり得ます。過学習の結果○○施策が有効だと思って大量の人月コストを投じてスマホアプリを改修したのに、いざリリースしてみたら全くCVが伸びない、とか。。。それが過学習した不適切なモデルのせいだった、なんてことになったら泣くに泣けません。
いかなる理由があったとしても、出来る限りモデルの精度は学習データに対する当てはめだけを見るのではなく、きちんと未知データ(テストデータ)への当てはめを見るようにするべきだという所以でもあります。
何故こんなことになるのか
これまた『はじパタ』でもPRMLでもバイアス=バリアンス分解の下りで詳細に書かれている話ですが、もう少し噛み砕いて見てみましょう。まず、3次多項式モデルと9次多項式モデルとを書き並べてみるとこうなります。
単純に読めば、3次多項式モデルは説明変数3つのモデル、9次多項式は説明変数9つのモデル、ということになります。一方、元のデータを生成した真の3次関数は以下のような形をしていました。
つまり、元データの背後にある真のモデルは「3次多項式のシグナル+ノイズ」という構成になっているわけです。ここにポイントがあります。
まず、真のモデルと次数が等しい3次多項式モデルであれば、ノイズにはフィットし切れないけれどもシグナルにはぴたりとフィットすると期待されるわけです。では、9次多項式モデルではどうなるかというと。。。そう、「シグナルにもノイズにもフィットしてしまっている」のです。つまり、「次数を上げた(説明変数を増やした)ことで学習データのシグナルだけではなくノイズにまでフィットしてしまった」ということなのです。当然のことながら、未知データはシグナルの真のモデルに沿って発生し、それにちょっとだけノイズが乗っただけの代物であるものと期待されるため*2、そんなめちゃくちゃなモデルで予測しようとしても当たるわけがありません。
一般に、今回例に挙げた多項式近似に限らず「モデルの説明変数は必要以上に増やせば増やすほど学習データのシグナルだけでなくノイズにまでフィットしてしまう」ということが言われています。試しに『はじパタ』同様に、今回の多項式データに対して1次, 2次, …, 9次まで次数を上げて各々モデル推定した時の、学習データ16点に対するMSE(平均二乗誤差)とテストデータ5点に対するMSEとを次数ごとにプロットしていくと以下のようになります。

既に見たように、3次でちょうど訓練誤差(対学習データ)とテスト誤差(対テストデータ)とがほどよく最小値を取っている一方で、特に5次以上に次数が上がっていくと訓練誤差は減り続けるのに対してテスト誤差はどんどん跳ね上がっていくのが分かるかと思います。
このように、闇雲に説明変数を増やしていくと確かに訓練誤差は下がる(学習データへの当てはめ精度は上がる)わけですが、実際にはテスト誤差は途中から上がっていってしまう(未知テストデータへの予測精度は下がる)わけです。なので、もし仮に上に書いたように「『予測』よりも『説明』を重視」した結果としてモデルの訓練誤差しか評価せず、なおかつその訓練誤差をさらに減らすために何も考えずにどんどん説明変数をこれでもかと増やしていったら。。。最悪ですね(汗)。モデルはでたらめ、パラメータ(変回帰係数)の推定結果もでたらめ、ということになって悪影響はもはや計り知れません。
交差検証でより汎化性能に優れたモデルを選ぶ
では、そのようなモデリングの現場においてそういう困った事態を避けるにはどうしたら良いのでしょうか? 最も確実なのは交差検証(cross validation)を行うことで、個々のモデルの汎化性能を評価することかと。
『はじパタ』でも触れられているように、交差検証には様々なやり方があります。例えば学習データをランダムに2つに振り分けて片方でモデルを学習させもう片方でその精度を評価するhold-out法、学習データをk個に分割してそのうちk-1個でモデルを学習させて残った1個でモデル精度を評価するのをk回繰り返すk-folds法、学習データのうちサンプル1つを抜いてモデルを学習させて残った1サンプルへのモデル予測値を比較するのをサンプルサイズの分だけ繰り返すLeave-One-Out法、他にもbootstrap法やランダムフォレストで用いられるOut-Of-Bag法などもあります。
今回の簡単な例では、試しにLeave-One-Out法でモデル評価してみます。学習データ16点の一つ一つに対して、残り15点から推定したモデルに基づいて予測値を出し、これをプロットして比べてみるということをしています。
# Leave-One-Out法で3次多項式モデル・9次多項式モデルそれぞれの # 交差検証データへの予測値を算出する > lm3_vec<-rep(0,16) > for (i in 1:16){ + tmp<-lm(y~V1+V2+V3,d[-i,c(1:3,10)]) + lm3_vec[i]<-predict(tmp,newdata=d[i,1:3]) + } > lm9_vec<-rep(0,16) > for (i in 1:16){ + tmp<-lm(y~.,d[-i,]) + lm9_vec[i]<-predict(tmp,newdata=d[i,-10]) + } # 学習データと見比べてみる > plot(x,y,cex=4,xlim=c(0,8),ylim=c(-80,120)) > par(new=T) > plot(x,lm3_vec,cex=4,xlim=c(0,8),ylim=c(-80,120),col='red') > par(new=T) > plot(x,lm9_vec,cex=4,xlim=c(0,8),ylim=c(-80,120),col='blue')

ほぼ学習データに追従している3次多項式モデルの赤い点に対して、9次多項式モデルの青い点は一部あさっての方向にぶっ飛んでます。これを見るだけでも、9次多項式モデルが過学習を起こしていて不適切だということは容易に分かるかと思います。
このように、交差検証を行うことで学習データのみしか手元にない状況であっても、過学習しておらずより汎化性能の高いモデルを選ぶことができる、というわけです。現実にはLeave-One-Out法は計算負荷が高くて必ずしも使えるとは限らないので、適宜hold-out法やk-folds法を選択するとよろしいかと。
他にも、L1正則化で要らない説明変数を削るという考え方もあります。正則化については下記の以前のブログ記事を参照のこと。実際にやってみた結果が以下。ちなみにここで正則化パラメータを求める際にも、cv.glmnet関数は交差検証誤差に基づいて最適値を決めています。
> lm_regL1<-cv.glmnet(as.matrix(d[,-10]),y,family='gaussian',alpha=1) > plot(lm_regL1) > coef(lm_regL1,s=lm_regL1$lambda.min) 10 x 1 sparse Matrix of class "dgCMatrix" 1 (Intercept) -6.811253828 V1 21.132445191 V2 -5.071913288 V3 . V4 . V5 0.005820756 V6 . V7 . V8 . V9 .
何故か3次の項が落ちてて、代わりに5次の項が入っちゃってますね(汗)。今回の例ではあまりうまくいかないようです。ただし過去記事のテニス四大大会データや冷暖房効率データではうまくいっているので、割と汎用的に使える手法だということは覚えておいて良いでしょう。
最後に
以上に述べてきたことは、もちろん多項式近似のような初歩的なテーマに限らず、線形回帰モデル(重回帰分析)、一般化線形モデル(ロジスティック回帰など)、サポートベクターマシン(SVM)、ランダムフォレスト、Xgboost、はたまたDeep Learningと言ったその他の統計モデリングand/or機械学習モデルのほぼ全てに当てはまります。上記の内容と全く同じような手続きで、過学習を回避し汎化性能を上げることができます。
ただし、統計モデリング系の手法であればAIC, BIC以下様々な情報量基準に基づいて解析的に汎化性能を評価する方法もあります。が、個人的な感想ながらそれだけでは交差検証には及ばないという印象もあります。。。なので出来る限り交差検証した方が良いかなぁと。
また、これは割と嫌な話ですが「交差検証したからと言って汎化性能が確保できるとは限らない」ケースもあるということ。特に学習データと(テストデータではない本当の)新規の未知データとで性質が全く違うようなケースでは、いかな汎化性能の高いモデルでも太刀打ちできません。時々Kaggleでその手のデータセットが出てきて物議を醸すことがありますが、実務でも同様のことは少なくないです。
そして似て非なるパターンとしては「交差検証したにもかかわらず過学習を起こしたままになる」ケースもあったり。特にサンプルサイズ(行数)に比して説明変数の個数(列数)が多い高次元のケースで、尚且つ可視化が困難なレベルの高次元だとそもそも過学習を起こしているかどうかも分からない、なんてことも。。。念には念を入れましょう、ということで。
なお、この記事は『はじパタ』2章やPRMLはたまたカステラ本と言った機械学習のテキストに出てくる、過学習&汎化性能の下りを超テキトーになぞっただけのものでして、例えばVC理論みたいな汎化誤差の理論解析とかそういう話はまっっっっったく念頭に置いておりませんので悪しからず。というか、むしろVC理論とか未だに全く理解できてないので誰か教えてください(泣)。もちろん、いつも通り炎上ラーニング大歓迎なので間違っている点などあればどしどしご指摘ください。
ちなみにもっと突っ込んだ機械学習の理論的な話題になったらその手の汎化誤差の理論解析とかも押さえておくことは重要なはずなので、そのうち勉強しようかなぁと。。。*3