追記
再現性をチェックする実験を後日実施しています。併せてお読みください。
以前こんな記事を書きました。
この辺の話はとっくの昔に常識になっていると思っていたのですが、昨今様々な「モデル」が提唱されて公の場で喧伝されることが増えてきており、その中には明らかにこれらの記事で指摘されている問題に引っかかっているものがあるようなので、注意喚起も兼ねて改めてブログ記事として書いてみようと思います。
追記 (May 08, 2020)
本文中にも記事公開当初の初稿の時点でいくつか但し書きを入れてありますが、この記事で最も強調したかったことは「時系列データに対して多項式フィッティングを行うという本来あり得ないモデリングのやり方であっても、交差検証を行えば短期的な予測性能(汎化性能)を改善することができる」ということです。データセットにランダムウォークを選択したのは、単に極値が2つ以上ある時系列を生成したかったというだけの理由であり、102という乱数シードは101から探し始めて2つ目で終わったというしょうもない過程を示しており、乱数シード自体には何の意味もなく、単にデータの生成プロセスを固定するという以上の意味はありません。そしてモデリング手法に多項式フィッティングを選択したのは、1) 他のモデルを例に出すのが面倒だった、2) ここでは交差検証すら知らない読者層を想定していてトレンド付き時系列モデルの説明などを追加すると逆に混乱を招くと判断した、3) Excelなどでも気軽に利用できるという点でそれらの読者層にも馴染みがある、4) 「後から作為的にどんどん特徴量を増やす」作業がやりやすい、5) あえて非現実的なモデリング手法を挙げた上でそれでも交差検証すると短期的な予測性能を改善できるということを示したかった、という理由に基づきます。なお「ランダムウォークに何とかして予測モデルを当てはめようとする絶望的な取り組みが実務における時系列モデリングの本質である」という深遠な事実を述べたかったわけではありません。
- 「データが増えるたびにモデルを更新して未来予測を行い、その予測を当てにする」ことの落とし穴
- あえて多項式フィッティングを汎化性能を重視し、交差検証しながらやってみる
- モデリングにおいて重要なのは「汎化性能」の概念と「交差検証」
- 終わりに
「データが増えるたびにモデルを更新して未来予測を行い、その予測を当てにする」ことの落とし穴
はじめに、ここではちょっとした架空の例をシミュレーションしてみることにしましょう。なお脅かすわけではありませんが、これにほぼ同じかそれに近いシチュエーションに陥って大変なことになった大企業が何社か実在することを予めお断りしておきます。
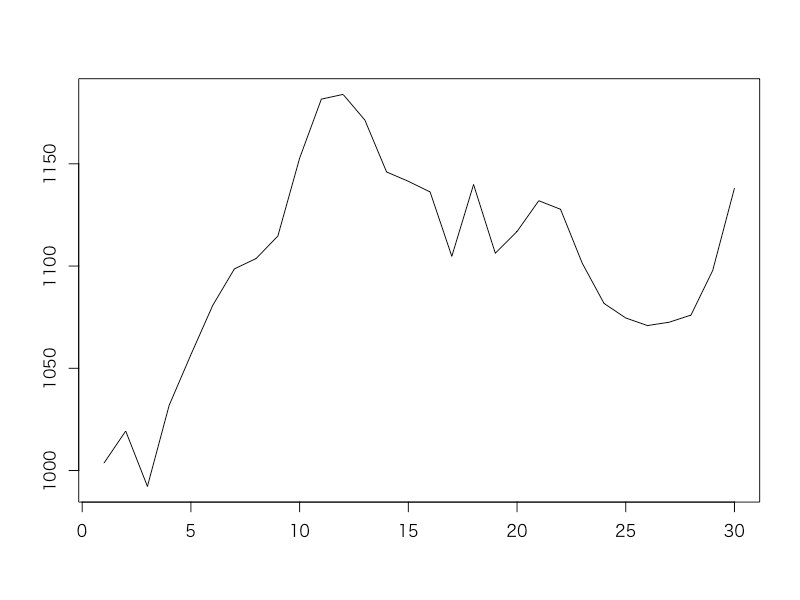
……ある小さな会社の過去30日間の看板商品の売上高がこんな感じのプロットになっていたとします。この会社の営業部長さんは、販促キャンペーンの都合上売上高の正確な予測ができた方が嬉しいと考え、Excel*1の「多項式フィッティング」という機能を使い、30日経過するごとにそれまでのデータに対して多項式フィッティングを行い、今後60日間の売上高の予測を行うことを考えました。名案を思いついた部長さんは、早速その分析を部下に命じてやらせます。
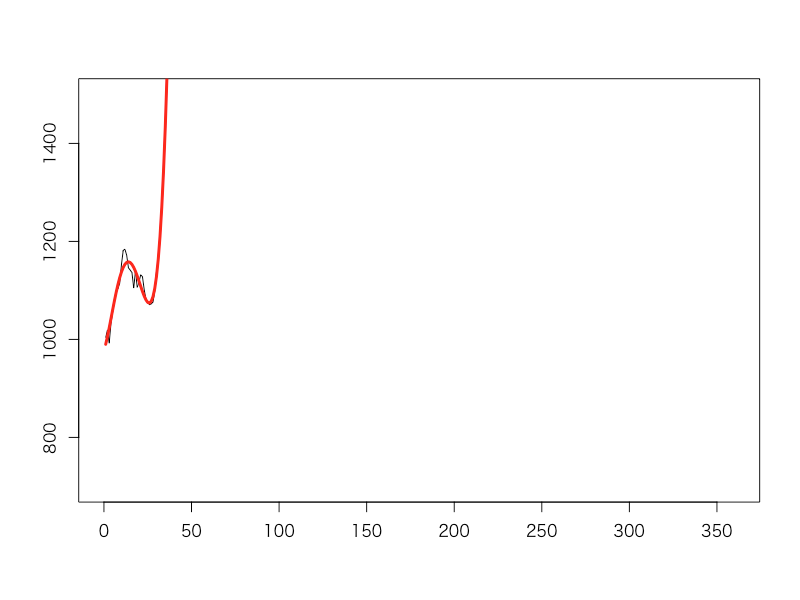
まず、最初の30日のデータをもとに営業部長さんは4次の多項式フィッティングをかけてみることにしました。すると、向こう60日間の売り上げは一気に高く伸びていくようだということが分かりました。「よし、これはガンガン広告を出してもっともっと売っていこう!」と部長さんは早速販促部に指示を出しました。
抜かりのない部長さんは、よりモデルを「精緻」にすることを考えていました。そこで部長さんが予測を担当する部下に行わせたことは「30日経過するごとに多項式フィッティングの次数を1つずつ増やしていく」ということ。こうすれば、この先もっと上下に売上高が振れて複雑な振る舞いをするようになったとしても、次数が増えてモデルが複雑になった分だけうまく当てはまってくれるはずだからです。
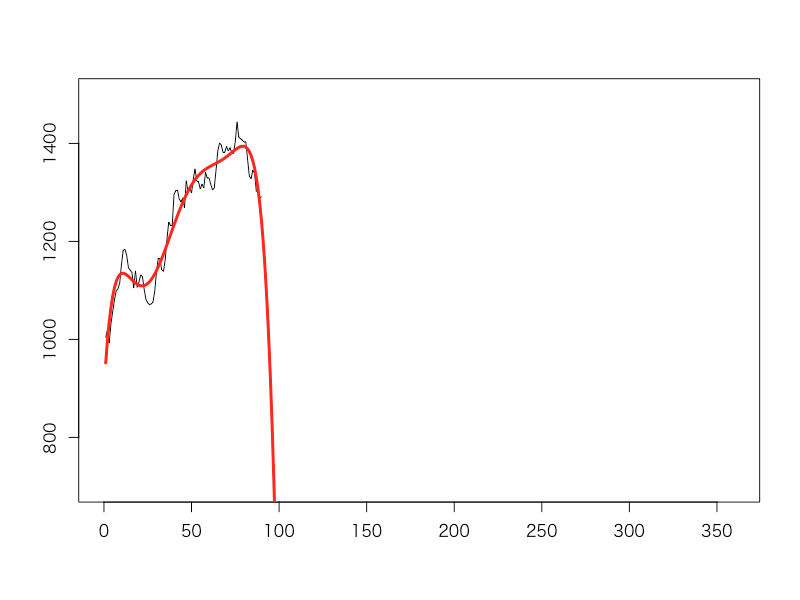
しかし、3タームが経過したところで部長さんは部下から見せられたExcelの画面を見て青ざめます。何と、この先売り上げは急降下してあっという間にゼロに向かって落ち込んでいくというのです。「こんなことでへこたれるわけにはいかない!広告を打つだけでなく内勤の人間まで含めて全員営業して回ってこい!」と号令をかけました。
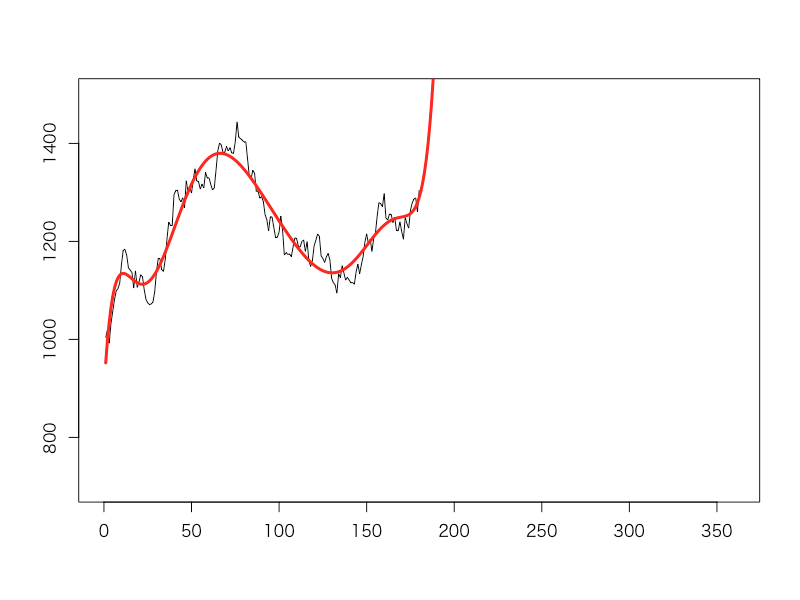
6タームが経過する頃には、彼らの努力の甲斐あってか売り上げも回復し、多項式フィッティングによる予測値もばっちり上向きになっていました。部長さんはご満悦の表情。「これで1年間売り上げ目標を達成し切れば、役員の座も狙えるかも?」と目を輝かせながらExcelの画面を見つめていました。
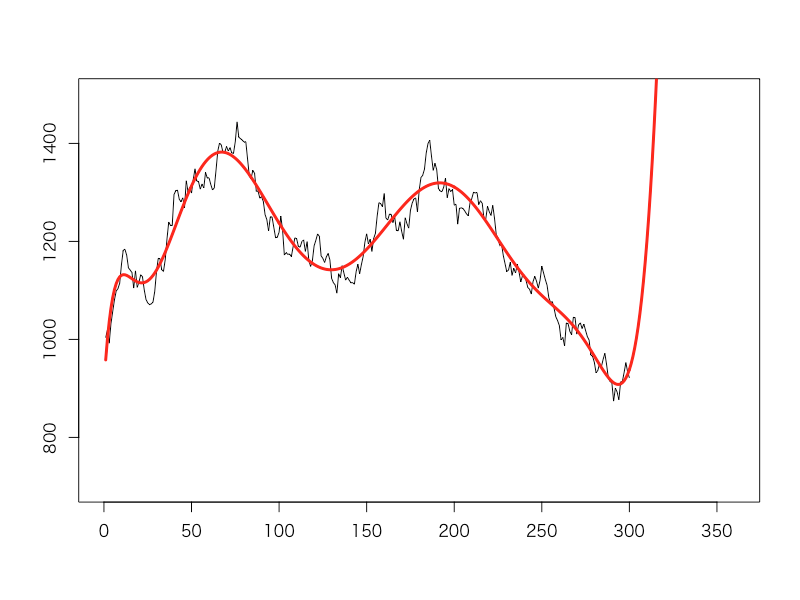
そして10タームが経過した後、部長さんは役員会に呼ばれた際に高らかにこう宣言します。「今まで我々はこの多項式フィッティングモデルを信じて頑張ってまいりました、そして売り上げ目標も達成してまいりました!ご覧ください、この高く伸びていく売り上げ予測を!今後は何も心配は要りません!」
……ところが。その2ターム後、社長室に呼ばれた部長さんは社長からこう言い渡されました。
「君は一体これまでの1年間何をやってきたのか?営業部長の職を解くので、明日からの社内での居場所は勝手に自分で探したまえ」
つまり、営業部長解任という衝撃の処分でした。それもそのはず、その後の2タームの結果は以下の通りだったからです。
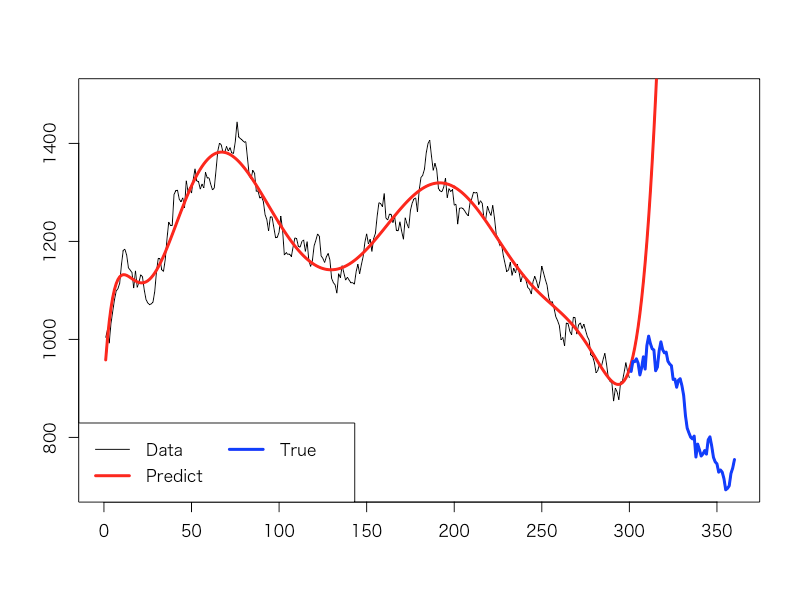
多項式フィッティングが示した高く上に伸びていく赤線の予想に対して、実際の売上高を示す青線は下降トレンド。完全に真逆の予測をしてしまっていたことが、社長の逆鱗に触れたのでした。それどころか、直近数タームの下降トレンドに対して多項式フィッティングの予測を過信し、何の対策も取ってこなかったことが問題視されたのでした。
けれども、部長さんは納得がいかない様子。「こんなはずないのに……これまでうちの部で手掛けてきた多項式フィッティングモデルは完璧だったはずなのだが……どのモデルも過去の実績データへの当てはまりはばっちりだったのに……」とぼやきながら、「業務改善部屋」へと荷物をまとめて向かって行ったのでした。
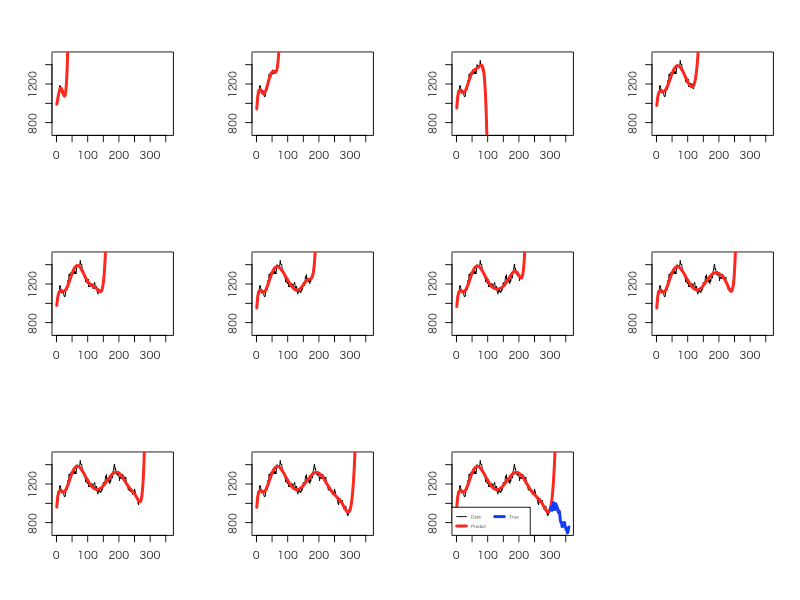
最後に、全10タームのそれぞれのタームにおける多項式フィッティングの結果を並べておきます。第6・7ターム辺り(つまり7・8次多項式モデル)では何となくフィットしていてその先の未来予測もまぁアリかもという雰囲気があるのですが、それ以降はどう見ても合っていません。謎の「根拠はありませんがこの先V字回復します!」的な予測になっています。これではどう見てもおかしいと言わざるを得ないでしょう。
つまり、ここで推定されていたモデルはいずれも過去のデータに対しては当てはまりが良かったものの、その先の未来のデータに対する予測の精度は悪かったわけです。未知(未来)のデータへの当てはまりの良さを一般に「汎化性能」と呼びますが、その汎化性能を全く考慮せずにひたすら過去データへの当てはまりばかりを重視して、尚且つ過去データへの当てはまりが良いモデルを未来予測にも優れていると誤認したがゆえに生じた悲劇だった、ということです。
このセクションで行ったシミュレーションは、こちらのrepoに上げたRスクリプトで実演したものです。各種パラメータを変えてみると、さらに異なる帰結に至って面白いかと思います。
あえて多項式フィッティングを汎化性能を重視し、交差検証しながらやってみる
それでは、どうすれば良かったのでしょうか? 今回題材に挙げたような時系列データに対して、素朴な多項式フィッティングを行うのはおかしいというか不適切なことが大半なのですが*2、ここではあくまでも例としてあえて多項式フィッティングで正しくモデル推定し、なおかつ適切に未来予測する方法を考えてみます。
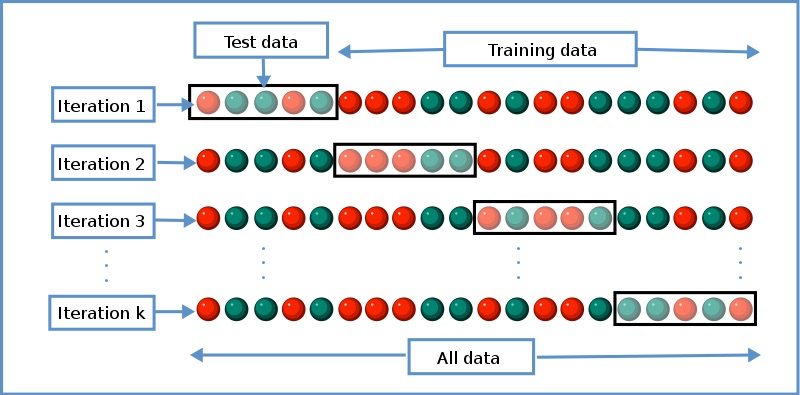
それは交差検証を行う、というものです。具体的には、最初から80%の時系列データを「学習データ」、残りの後ろ20%を「検証データ」とし、最大で例として20次までの多項式フィッティングモデルを予め用意した上で検証データへの当てはまりが最も良かった次数のモデルを選ぶ、という方法をここではとります。本来は歯抜けになるように不要な次数の項も削除するようなステップワイズ法を使うべきなのですが、それをやるくらいならL1正則化すれば良いとかもっと良い代替手段が沢山出てきてしまうので*3、ここでは割愛します(笑)。

すると、こうなります。第8タームなどでは多少予測値が暴れる感じがありますが、概ね各タームごとでの最新のデータに合わせて相応に当てはまりも良く、尚且つその次の60点のデータの予測についてもやはり相応に精度の良いモデルが選ばれていることが見受けられます。
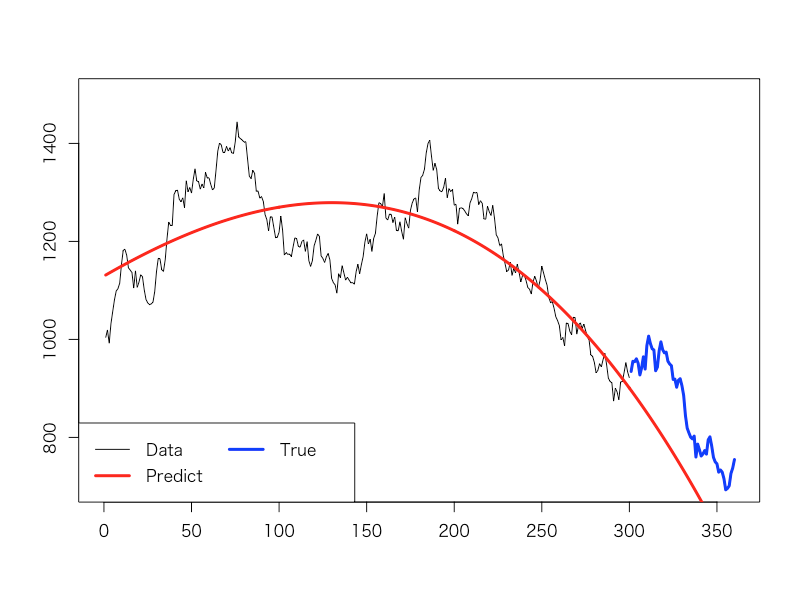
最終的に第10タームで採用されたモデルも、そこそこ適切に下降トレンドを予測できていることが分かります。ちなみにこれはただの2次式のモデルです(笑)。同様の凹型関数である4次とか6次とかにならない辺りに、こういう多項式フィッティングモデルの精度の悪さを感じなくもありません……ともあれ上記の喩えに出てきた部長さんよりは、汎化性能に優れて未来予測に有用なモデルを選べている、ということが見て取れると思います。
なお、こちらのrepoに上げたRスクリプトで全く同じ交差検証を行いながら多項式フィッティングさせる様子を追体験できます。意外と積極的に不要な項を落としまくらなくても、次数に上限を嵌めるだけでそこそこの結果になることが分かります。
モデリングにおいて重要なのは「汎化性能」の概念と「交差検証」

冒頭に再掲した以前の記事でも論じていますが、基本的にどんなやり方をするにせよ、この宇宙における何かしらの現象をモデリングで表現して予測に用いるのであれば、いかなるモデルであろうとも「汎化性能」の概念が最重要です。どれほど学習データへの当てはまりが良いモデルであろうとも、未知のテストデータへの予測の精度が高いことが重要である、という考え方です。
例えば、上記は冒頭に挙げた過去記事の中で、真のモデルが3次式というデータに対して多項式フィッティングを行い、学習データへの誤差と検証データへの誤差とをモデルの次数を上げながらプロットした例ですが、学習データへの誤差は9次まで次数を上げると減っていく一方で、検証データへの誤差は明らかに3次で最小になっています。つまり3次より高次のモデルは真のデータではなく、ノイズにまでフィットしているということです。
以前某所で登壇した時にも話しましたが、分かりやすい喩えとして「受験勉強と大学入試問題」との関係があります。一般に、大学入試の過去問(学習データ)の解き方を沢山勉強すれば、過去問は確実に解けるようになります。しかしながら、過去問を沢山勉強したからと言って、本番の新たな入試問題(テストデータ)を確実に解けるとは限りません。毎年毎年新たに考案されてやってくるまだ見ぬ本番の入試問題を解けてこそ、意味がある。全く同じことが、各種のモデリングにおいても言えます。
(By Gufosowa - Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=82298768)
それを確かならしめる方法論の一つが、繰り返しになりますが交差検証です。これにより、学習データにだけ当てはまりが良く未来予測に適さないモデルを排し、真に未来予測に貢献し得るモデルを選ぶことができます。具体的には、例えばデータ全体の中から80%を選んできて学習データとし、残り20%を検証データとし、前者でモデリングを行った上で後者を予測し、その予測誤差に基づいてモデルのチューニングを繰り返し、得られたベストモデルをデータの外側にある未知データの予測に用いる、というようなやり方です。
ただ、時系列データの予測に関しては通常のモデリングとは異なり「学習データは必ず過去方向に置き、検証データ&テストデータは必ず未来方向に置く」という制約がかかります*4。この点については上記の過去記事2件もご覧ください。理論上も実践上もこれがベストの方法とは限らないのですが、実務的にはこれが「よりマシ」な解決策であることを申し添えておきます。
大事なことは、ここで挙げた「汎化性能」「交差検証」の考え方は多項式フィッティングのようなプリミティブなモデルに限らず、重回帰分析のようなシンプルな統計モデルからDeep Learningを含む高度な機械学習モデル、はたまたベイズ統計を駆使した複雑な統計モデルに至るまで、いかなるタイプの「予測モデル」にも当てはまる、ということです。何かを「予測」するために用いられるモデルに対しては、必ずここで例示したような方法論で検証しないと、往々にして使い物にならないのです。
言い方を変えれば、何の根拠もない多項式フィッティングですら交差検証すればそれなりに汎化性能のあるモデルにたどり着けるということを、上記の例は示しているとも受け取れます。いかなるモデルであれ、「予測」*5のために使うのならば、必ず交差検証しなければならないということです。