気が付いたら僕がデータ分析業界に身を置くようになってそろそろ5年近くになるんですね*1。この5年間の間に色々勉強したり業界内で見聞してきた経験をもとに、「実務の現場においてモデリングを行う上での注意点」についてだらだらと書いてみようと思います。
と言うのも、色々な現場で様々なモデリング(統計学的にせよ機械学習的にせよ)が行われていることが伝わってくるようになった一方で、ともすれば「え?こんな基礎的なポイントも守ってないの?」みたいなとんでもないモデリングがまかり通る現場があると愚痴る声を業界内で聞くことが少なくないので。自戒の意も込めて重要なポイントを備忘録としてブログ記事にまとめておくのも有益かなと思った次第です。
この記事では手法選択(線形・一般化線形・ベイズ+MCMC・識別関数・識別モデル・生成モデル・樹木モデル・Deep Learning etc.)の話題は割愛しました。一般に、モデリングの多くは手法選択以前のメタな問題設定の部分でそのクオリティが決まってしまいがちなので、そちらをこの記事では重視しています。ただし、時系列データだけはそうもいかないため若干手法ドリヴンな問題提起をしています。
あ、いつも通り炎上ラーニング上等(笑)で書いてますので、僕よりずっともっと詳しい方々*2からのマサカリを心よりお待ちしております。多分どこかしら間違っていると思いますので、皆様の集合知を頼りにより良くより正しい内容に改めていければ有難いです。
汎化性能:きちんと未来の予測に役立つのか、そして過去データのノイズに過学習していないか
これはもう過去記事でも散々やったことですが、要は得られたモデルが「真のシグナルにきちんとフィットしている」か「ノイズにまで過剰にフィットしている」かの違いだと言って良いでしょう。

これは「黄色い本」でもお馴染みの多項式フィッティングをなぞったもの。x座標を1-9乗したものを説明変数として用意して、どの組み合わせがベストモデルかを探すというアレです。黒丸で表される学習データ15点に対して、「1次+3次モデル」(赤線)と「9次のフルモデル」(青線)を旋回回帰モデルで推定して、の範囲で500点のグリッドを切ってプロットしたものです。学習データ15点に対するRMSEは「1次+3次モデル」で6.45に対して「9次フルモデル」で2.38ということで、「9次フルモデル」の方が学習データへの当てはまりの方が良いということになっています*3。
しかしながら実際の全体のデータを表したのが白ヌキ丸50点で、これを生成した真のモデルはというものなので、赤線の「1次+3次モデル」の方がより真のモデルに適合するはずです。実際、汎化性能を確かめるためにLOO (Leave-One-Out) cross validationを行なってそのRMSEを見ると「1次+3次モデル」で8.98、「9次フルモデル」で10.79となっていて、確かに前者の方が汎化性能が高いことが分かります。そしてそれは、上記プロットを見れば一目瞭然です。
にもかかわらず、実務の現場では汎化性能を無視して学習データへの当てはまりだけを見てモデリングをしてしまい過学習に陥っているケースがかなり多いと、色々なところで伝え聞きます。「過去データにこれだけぴったり合ってるんだからいいじゃないか」「これ以上一つのモデルに手間なんてかけてないで別のテーマの分析に取り掛かってくれ」という掛け声のもと、汎化性能がないがしろにされる現場もあるようです。当たり前ながら、そのような過学習したモデルを使っていては推定されたパラメータに基づく未来のアクションの意思決定にせよ、モデルに基づく未来値予測にせよ、どんどん実データからかけ離れていくのは必至です。けれどもそういう現場に限って「これは使っている変数が足りないからだ、もっと変数を増やそう」とさらに過学習を悪化させるケースが多いそうで。。。
ということで、モデリングを行うからには汎化性能を確保することが第一義です。AICなどの情報量基準で判定するにせよ、LOOを初めとするcross validation(交差検証)で検証するにせよ、とにかく「より汎化性能の高いモデル」を採用することを最優先にするべきでしょう。
解釈性と予測性:「ヒトの意思決定のため」なのか、それとも「システム出力のため」なのか
実務の現場におけるモデリングは、言うまでもなくビジネスに直結することが多いです。ここでのポイントは「そのモデルがビジネス上どう使われるか?」によって、モデリング自体のやり方も変わってくるということ。
今年6月の講演*4では「Interpretability(解釈性) vs. Predictivity(予測性)」というタイトルで、まさにこのポイントについて論じました。一般に、ビジネスの実務でモデリングをする際には大別して
- Modeling for Human: モデルのパラメータ(偏回帰係数など)の正負や大小などをエビデンスとみなして責任者が意思決定する
- Modeling for Machine: eコマースシステムにおけるレコメンデーションや動的コンテンツ生成などのシステム出力をモデルに基づいて行う
の2種類に分けられると思われます。この場合、前者については偏回帰係数などのパラメータが陽に求まらないモデルは使えませんが、その分例えば予測精度は低めでも良いと言うシチュエーションがあり得ます。一方、後者についてはパラメータ不明なブラックボックスでも問題ありませんが、その分予測精度は高くなければいけないことが多いように聞きます。
この2要素はある程度トレードオフとしての側面がある*5ので、どちらを優先するか?というのは結構モデリングを始める段階でかなり重要なポイントになるはずだと個人的には考えています。また、最近では自動運転技術の文脈でも時々言及されますが「万一事故などの問題があった際の原因究明*6に役立てるために」モデルの解釈性が高い方が良いという考え方も出てきているようです*7。例えば「もっと映像の中の『暗い』部分を重視すべきだ」というような議論ですね。そういう観点から言っても、解釈性と予測性のどちらを優先させるか・どうバランスさせるかも重要なファクターだと言えると思います。
変数間の因果の向きと内生性:「それ、原因と結果逆じゃないの?」

経済学クラスタの方々からは「そんなの常識だろ」というツッコミを某所でいただきましたが、これって実務の現場でモデリングする際には驚くほど軽視されがちなポイントだったりします。
モデリングをする際、統計学的にやろうと機械学習的にやろうと各々の変数が外生的(exogenous: こちらから操作できる)なのか内生的(endogenous: こちらから操作できない)なのか、もしくはその辺を一般化した内生性(endogeneity: 説明変数と誤差項との間に相関があり説明変数としては信頼できないことを指す)の問題*8について知ることは非常に大事どころか、文字通りイロハのイだと思います。特にオーソドックスなマーケティングモデルであれば外生変数を説明変数に、内生変数を目的変数に置いて、説明変数→目的変数なる因果の向きが出来るようにするはずです。
特にこれが"Modeling for Human"である場合、(例えば)個々の施策を表現するパラメータの正負や大小によって、その施策の優先順位を変えるといった使われ方をすることが多いはずです。小売店舗の売り上げモデル(日次売り上げが目的変数)において「商品陳列レイアウトA」のパラメータが「レイアウトB」のパラメータより大きければ前者をより多くの店舗で推進する*9、というようなイメージですね。言うまでもなく商品陳列レイアウトはこちらから操作できる変数すなわち外生変数の代表例であり、この大小でアクションを決めるのはごく自然なことだと思います。
ところがこういうモデルにしれっと内生変数が混じったり、因果の向きがおかしな変数の組み合わせが混じったりすると、話がおかしくなります。例えば上記の小売店舗の売り上げモデルで言えば「来客に占める子供の割合」みたいな変数は、こちらから操作できそうかというと意外とそうでもなくて、別の方向性のアクションがないと操作できないはずです。また同じ小売店舗のモデルでも「日次来客数」を目的変数にすると、商品陳列レイアウトの良し悪しが果たして因果的影響を及ぼすかというと、難しい気もします。ちなみに前者後者どちらのケースでも、本来変数に置くべきはおそらく「広告」になるかと。
小売店舗のモデルのようなシンプルな話であれば混乱する人は多くないと思いますが、実際にはもっと複雑なマーケティングモデルになると割と混乱する人が多い印象があります。「いやいやその説明変数どう見ても目的変数からの影響受けてるやつじゃん」みたいなケースは珍しくないようです。思いつきで変数を加えていくようなことはせずに、きちんとまずは因果の向きと内生性をひとつひとつチェックしていきましょう*10。
追記(2017/09/27)
id:takehiko-i-hayashi先生が「内生性・交絡」について非常に分かりやすい記事を公開なさっていたので、ここに追記としてリンクしておきます。この「本来目的変数に対する説明変数であるべき変数が、別の変数に対して左辺(つまり潜在的な目的変数)に現れる形で表せてしまうケース」という説明には個人的には納得がいきます。また、これに該当する例としてVARモデルで相互に自己回帰で表せるような2つ(以上)の時系列データを挙げることができることを鑑みると、どういう時に内生性が生じるかというイメージが確立できそうな気がします。
時系列データなら自己相関・単位根・共和分をチェック:「見せかけの回帰」に振り回されないように

これだけちょっと手法選択の問題が関わってきます。一般に、単なる受給予測のような「内生変数だらけでも構わないので未来予測がしたい」みたいなケースで、時系列データをモデリングすることは世間ではよく行われているようです。しかしながら、ここにも色々な問題が潜んでいます。
僕が知る範囲で最もあるあるなのは、例えば上の図のような時系列データ同士で普通に線形回帰モデルをやってみたら全てのパラメータが統計的に有意で「よっしゃこのモデル完璧じゃん!これさえあれば幾らでも正確に予測できるぞ!」みたいな結論になる、というケースです。ここでは赤線が目的変数、青と緑の破線が説明変数だとします。そこで、この時系列データの80%で線形回帰モデルを推定して、そのモデルで目的変数の残り20%を予測すると。。。

はい、全然ダメですね(笑)。モデルの推定結果からは、パラメータ2つともばっちり有意*11でうまくいきそうだとしか思えないのに、どう見ても予測がうまくいっているようには見えません*12。
これは以前にも紹介したように、自己相関(系列相関)が強い単位根過程同士で線形回帰を行ったがために生じる「見せかけの回帰」という現象です。
実際、上の図の例だと3つの時系列全てが単位根過程検定にかけると「単位根である」という結果になるため、明らかに見せかけの回帰を起こしています。このような事態を避けるためには対策として
- まず単位根過程検定などで単位根過程が混じっていないかどうか調べる
- もしそうであれば
- 差分系列データに直してから線形回帰する
- 通常の線形回帰ではなくVARモデルを推定する
- 共和分関係があるとVARモデルは不正確になるのでその場合はVECMに移行する
- さもなくば動的線形モデルなどでトレンド要素も盛り込んだモデリングを行う
といった手段を講じる必要があります*13。もちろんこれらをやりさえすれば万全ということはありませんが、漫然と時系列データ同士で線形回帰して見せかけの回帰にハマるよりはマシだと思いますし、実際に予測精度もある程度は確保できるはずです。
因果推論が必要か否か:目の前にあるデータは交絡要因の影響を受けていないか
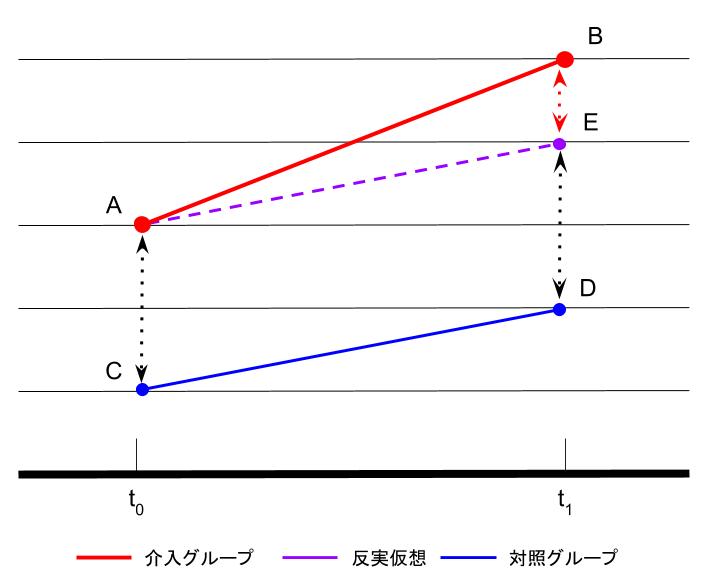

これはどちらかというとデータの「持たせ方」に由来する問題であり、分析そのものというよりそれ以前のメタな問題だとも言えるかもしれません。要は、何かの介入効果とか何かのグルーピングによる効果の有無をモデリングで明らかにしようと思った場合に、そもそもそれらの介入の裏側に厄介な交絡要因(因子)があって、何も考えずにモデル推定してパラメータを算出するとおかしな結果になってしまう可能性があるというお話です。これについては上記リンクの通り、このブログでもしばらく連続して取り上げました。
モデリングに関して言えば、岩波DS3の「TVCM接触の有無とスマホアプリ利用状況のデータセット」に出てくる例が最も分かりやすいでしょう。そもそもTVCMに接触するか否かというメタな介入ポイントに個々の家庭の家族構成のような交絡要因が関わることによって、一切の調整なしにモデル推定をするとおかしな結果*14が得られてしまうという手強いデータセットです。

- 作者: 岩波データサイエンス刊行委員会
- 出版社/メーカー: 岩波書店
- 発売日: 2016/06/10
- メディア: 単行本(ソフトカバー)
- この商品を含むブログ (4件) を見る
この本のpp.98-99には、ズバリ傾向スコアによる調整を行なったことで正しい線形回帰モデルの推定結果が得られた例が挙げられています。このように、モデリングの前提となる説明変数の裏側に何かしらの交絡要因があり得る状況では、因果推論の枠組みによるアプローチが必要だと言えると思います。
最後に
色々論ってみましたが、なかなかそんなところまでは手も気も回らないというのが実務の現場の実情なのではないかと思いますし、自分でもそこまで手が回らないことも多いです。それでも気をつけるべきところに気をつけることで、きちんと「実際に役立つモデル」を生み出していけるのではないかなと信じています。
あと、書き終わってから読み返してみたら、結局ほとんど統計学的なモデリングの話題しかしていないことに気付きました。。。まぁ機械学習モデルについてはどなたか僕よりももっと相応しい方が書いて下さるだろうということで、お後がよろしいようで。
*1:つまり5歳近く歳取ったわけで。。。
*3:スペースの都合上モデル計算の詳細は割愛します
*4:現所属先の方針により今後も講演資料は非公開とさせていただきます
*5:もちろん工夫次第では両立も可能だとは思いますが
*6:例えば「どの特徴量が良くなかったのか」
*7:今年6月の講演ではもっと具体的かつ深刻な仮想例を挙げましたが、ここでも言及はできませんごめんなさい
*8:経済学などで言うところの定義よりももっと大雑把に一部を切り取った説明なので、細かいところはより経済学などに詳しい方々の説明を仰ぎたいと思います。この辺も基本的には後述する、交絡要因(因子)とどう向き合うかという問題と関連します
*9:役員会で決定して事業本部に回す的な感じ
*10:その延長上に例えば操作変数法のような方法論があるわけですが、ここではスペースの都合上割愛します。詳しくはおそらくhttp://www.anlyznews.com/やhttp://ill-identified.hatenablog.com/あたりの方々からのツッコミがあるかと思いますので、そちらをお待ちください(汗)。ただし、冒頭に述べたように実務の現場だと予測性能を重視する傾向が強く(汎化性能の話題を挙げたのもそのため)、その場合はむしろこの後に述べるVARモデルやVECMはたまた傾向スコアのような手法を導入する方が適切とされるようです
*11:スペースの都合でモデル推定結果はここでは示しません
*12:本来ならば全て内生変数なのでこのような予測はできませんが、モデルが誤っていることを示すために便宜的に説明変数の未来値が得られる状況を仮定しています
*13:それぞれの対策についての詳細はスペースの都合上ここでは割愛します(こればっかり)