これは実は既に元ネタのあるテーマです。
個人的にはトレンド・季節調整付き時系列データの回帰モデルをやる場合はほぼ例外なくベイジアンモデリングで回すんですが、一般にベイズ系のモデルは例えばWAICやWBICのような情報量基準でモデルの汎化性能を推定することでモデル選択することができます。ところが、トレンド・季節調整付き時系列データのように回帰部分の尤度だけでは表せない、強い自己相関のある部分が大きいデータの場合は、モデル全体のWAICやWBICを算出する方法が(まだ?)ありません。
ということで交差検証(CV: cross validation)大好き人間の僕としては、普段は適当に「学習データ:古い方から80% / 検証データ:新しい側の残り20%」みたいなholdout CVしかやっていないんですが、当然ながらこれだけではholdoutの取り方によって差がつくため、どうしても恣意性が残ってしまいます。
そんな疑問を持っている時に、人から紹介されたのが上記のリンク先記事。こちらでは"sliding window"を用いたCV方法を提案しているということなので、これを実際に自分でクソコード書きながらやってみようかと思います。
交差検証のやり方
言ってることは簡単で「元データがn点ある場合、例えば交差検証データにk点確保するとしたら『学習データをn-k点&逐次交差検証データをn-k+1番目の1点のみ』→『学習データをn-k+1点&逐次交差検証データをn-k+2番目の1点のみ』→……」と1点ずつ学習データを増やしながら回帰しては交差検証をk回繰り返し、そのk回分の交差検証で得られた予測値と実測値とのRMSEを比較して比べる、というものです。
これもholdoutの取り方による恣意性を若干残しますが、それでも1点ずつ交差検証することによって例えばholdoutにおいて二階差分線形トレンド部分や季節調整部分を予め決め打ちにしてしまうことに由来する「本来交差検証であるはずなのに何故か事前にholdoutとして確定している(自己相関の強い)部分」の影響を多少は弱めることができます。逆に言うとモデルにある程度交差検証が本来的に持つ不確定性みたいなものを持たせられるのかなと。
なお、上記リンクには「さらにラグを空けて学習データのm点先の時刻の値を交差検証対象とする」というやり方も紹介されていましたが、これはコード書くのが面倒なので今回は割愛させていただきますということで、悪しからず。
単に全データで回帰した場合
これは以前にもほぼ同じことをやったことのある例なので、コードだけ並べておきます。ちなみに全てのコードはGitHubに上げてあります。適当にcloneするなりDLするなりしてお使いください。
そうそう、この記事以降基本的にこのブログにおけるStanのバージョンは2.15以上になっていますので、過去の2.10以前のバージョンで書いた記事とはStanスクリプトの文法が変わっています。ご注意ください。
data {
int<lower=0> N;
int<lower=0> M;
matrix[N, M] X;
real<lower=0> y[N];
}
parameters {
real season[N];
real trend[N];
real s_trend;
real s_season;
real s_q;
vector<lower=0>[M] beta;
real d_int;
}
model {
real q[N];
real cum_trend[N];
for (i in 7:N)
season[i]~normal(-season[i-1]-season[i-2]-season[i-3]-season[i-4]-season[i-5]-season[i-6],s_season);
for (i in 3:N)
trend[i]~normal(2*trend[i-1]-trend[i-2],s_trend);
cum_trend[1]=trend[1];
for (i in 2:N)
cum_trend[i]=cum_trend[i-1]+trend[i];
for (i in 1:N)
q[i]=y[i]-season[i]-cum_trend[i];
for (i in 1:N)
q[i]~normal(dot_product(X[i], beta)+d_int,s_q);
}
d <- read.csv('sample_marketing.csv') dvar <- d[,-1] dat <- list(N=nrow(d), M=ncol(dvar), y=d$cv, X=dvar) library(rstan) rstan_options(auto_write = TRUE) options(mc.cores = parallel::detectCores()) fit <- stan(file='sample_marketing.stan', data=dat, iter=1000, chains=4) slength <- 2000 dvar <- d[,-1] fit.smp<-extract(fit) t_d<-density(fit.smp$d_int) d_int<-t_d$x[t_d$y==max(t_d$y)] beta<-rep(0,ncol(dvar)) for (i in 1:ncol(dvar)) { tmp<-density(fit.smp$beta[(slength*(i-1)+1):(slength*i)]) beta[i]<-tmp$x[tmp$y==max(tmp$y)] } trend<-rep(0,nrow(dvar)) for (i in 1:nrow(dvar)) { tmp<-density(fit.smp$trend[,i]) trend[i]<-tmp$x[tmp$y==max(tmp$y)] } season<-rep(0,nrow(dvar)) for (i in 1:nrow(dvar)) { tmp<-density(fit.smp$season[,i]) season[i]<-tmp$x[tmp$y==max(tmp$y)] } beta_prod<-rep(0,nrow(dvar)) for (i in 1:ncol(dvar)){beta_prod<-beta_prod + dvar[,i]*beta[i]} pred <- d_int + beta_prod + cumsum(trend) + season matplot(cbind(d$cv, pred), type='l', lty=1, lwd=c(2,3), ylab='') legend('topleft', legend=c('Data', 'Fitted'), lty=1, lwd=c(2,3), col=c(1,2))

皆さん見慣れた二階差分線形トレンド+7日間季節調整つきの回帰結果になっているはずです。
交差検証しながら回帰した場合
多分Stanのところでもっと綺麗に書くことができるはずなんですが、僕はStanはまるっきり我流でしか書けない素人なのでひたすらR側で交差検証のところを網羅させたクソコードになってしまっていますorz 一応、簡単に回せるようにまずデータセット全体を7の倍数の98行までカットした上で、学習データが91点以降&交差検証データが残りの7点になるようにしています。
d <- read.csv('sample_marketing.csv') d <- d[1:98,] # Adjust the length of the dataset to 7days seasonality tl <- 7 # length of test period validate <- rep(0,tl) library(rstan) rstan_options(auto_write = TRUE) options(mc.cores = parallel::detectCores()) for (k in 1:tl) { d_train <- d[1:(nrow(d)-tl+k-1),] d_test <- d[(nrow(d)-tl+k),-1] dvar <- d_train[,-1] dat <- list(N=nrow(dvar), M=ncol(dvar), y=d_train$cv, X=dvar) fit <- stan(file='sample_marketing.stan', data=dat, iter=1000, chains=4, verbose=F) slength <- 2000 fit.smp<-extract(fit) t_s<-density(fit.smp$s_trend) s_trend<-t_s$x[t_s$y==max(t_s$y)] t_s<-density(fit.smp$s_season) s_season<-t_s$x[t_s$y==max(t_s$y)] t_s<-density(fit.smp$s_q) s_q<-t_s$x[t_s$y==max(t_s$y)] t_d<-density(fit.smp$d_int) d_int<-t_d$x[t_d$y==max(t_d$y)] beta<-rep(0,ncol(dvar)) for (i in 1:ncol(dvar)) { tmp<-density(fit.smp$beta[(slength*(i-1)+1):(slength*i)]) beta[i]<-tmp$x[tmp$y==max(tmp$y)] } trend<-rep(0,nrow(dvar)) for (i in 1:nrow(dvar)) { tmp<-density(fit.smp$trend[,i]) trend[i]<-tmp$x[tmp$y==max(tmp$y)] } season<-rep(0,nrow(dvar)) for (i in 1:nrow(dvar)) { tmp<-density(fit.smp$season[,i]) season[i]<-tmp$x[tmp$y==max(tmp$y)] } val_trend <- rep(0,3) for (i in 1:2) { val_trend[i] <- trend[nrow(d_train)-i] } val_trend[3] <- 2*val_trend[2] - val_trend[1] + rnorm(1,0,s_trend) val_season <- season[k] + rnorm(1,0,s_season) validate[k] <- d_int + cumsum(trend)[nrow(d_train)] + sum(d_test*beta) + val_trend[3] + val_season } (rmse <- sqrt(sum((validate-d$cv[(nrow(d)-tl+1):nrow(d)])^2) / tl)) matplot(cbind(d$cv[(nrow(d)-tl+1):nrow(d)], validate), type='l', lty=1, lwd=c(2,3), ylab='') legend('topleft', legend=c('Validate', 'Predict'), lty=1, lwd=c(2,3), col=c(1,2))
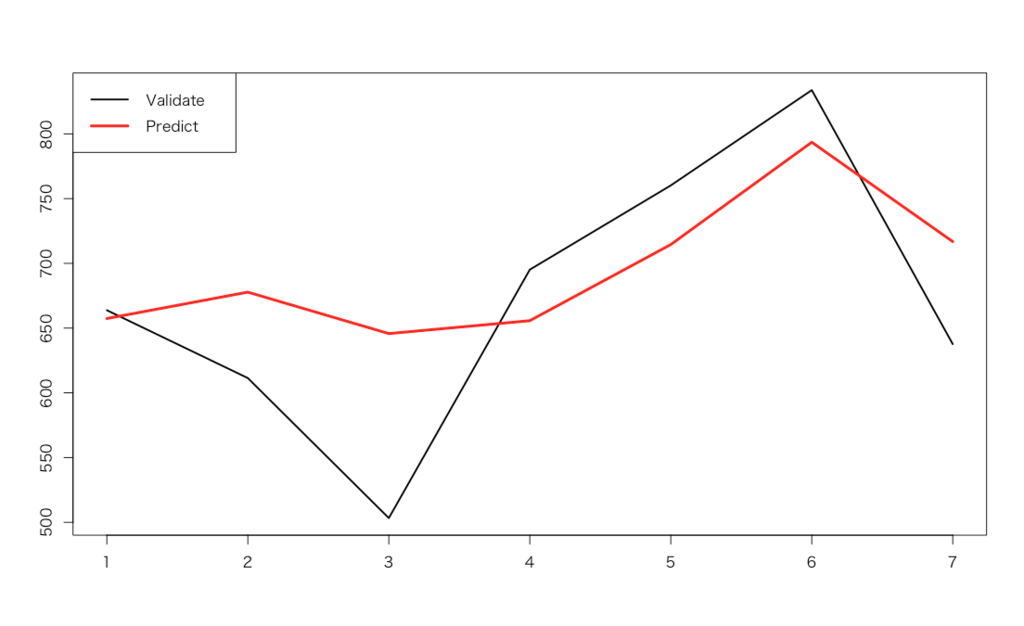
RMSEは71.98914という結果になりました。ちなみに、これを例えば元のデータセットから"ad1"を削除したものでやってみると以下のようになります。
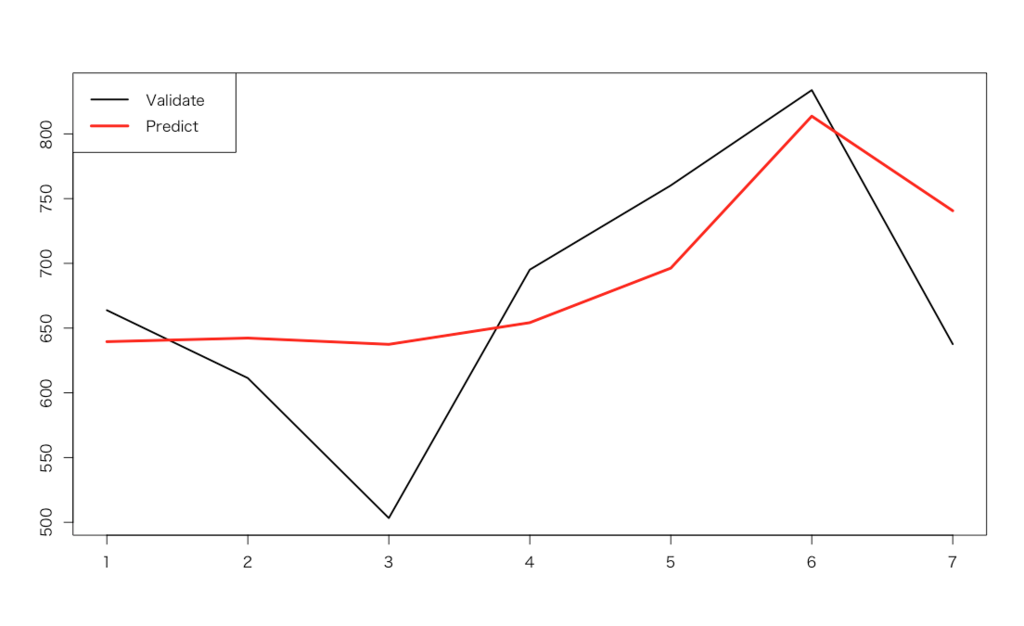
そしてRMSEは72.03332。僅差ではありますが、やはり説明変数は3つともあった方が良さそうです。という感じの「やってみました」報告ということで、お粗末様でした。