実はこのネタは元々別のところでやり取りのあった話題だったりします。
色々な都合があってここ最近{CausalImpact}に触れる機会が自分に限らず周囲でも増えているのですが、若い人たちから「そもそも{CausalImpact}って何をしているんですか?使う際は何に気を付けたら良いですか?」などと聞かれることがちょくちょくあるので、備忘録も兼ねてまとめてみることにしました。いつもながらですが、内容に不備や誤解や理解不足がありましたらどしどしご指摘くださいm(_ _)m
なお、{CausalImpact}パッケージそのものの簡潔な説明は随分昔に書きました。単純に使いたいだけならこちらの記事をお読みいただければ十分かと思います。
- {bsts}をバックエンドとして動く、統計的因果推論を目的としたcounterfactual modelingフレームワーク
- どのようにcounterfactual modelingしているのか
- 厳密には「差分の差分法」(DiD)を前提としていないが、事実上DiDを要求している
- 余談:共変量がなかったらどうなるのか
{bsts}をバックエンドとして動く、統計的因果推論を目的としたcounterfactual modelingフレームワーク
基本的なアイデアは以下の2つの公式資料に全て載っています。
やっていることは以前のブログ記事でも紹介したように、
キャンペーンの影響を受けていると思しき目的変数の時系列データに対して、1) 影響を受けていない他の共変量となり得る時系列と、2) キャンペーン期間を表すベクトル、を用意して、キャンペーンの影響を受けなかったと仮定した場合の目的変数の予測値を状態空間+MCMCで算出し、実測値と比較することでキャンペーンの因果的影響の大きさを見る
即ち目的変数の時系列データのcounterfactual(反実仮想)の値を用意して、これを目的変数の実測値の時系列と比べることで、どれくらい介入効果があったかを知るというものです。これはいわゆる統計的因果推論に属する考え方で、例えば僕が刊行委員として参画した岩波データサイエンスvol.3では反実仮想とは何かについて様々な解説がなされています。

- 作者: 岩波データサイエンス刊行委員会
- 出版社/メーカー: 岩波書店
- 発売日: 2016/06/10
- メディア: 単行本(ソフトカバー)
- この商品を含むブログ (4件) を見る
ところで、{CausalImpact}の使い方自体は以前のブログ記事に書いたように以下のような極めて単純なものです。
library(CausalImpact) set.seed(1) x1 <- 100 + arima.sim(model = list(ar = 0.999), n = 100) # x1は共変量(説明変数) y <- 1.2 * x1 + rnorm(100) y[71:100] <- y[71:100] + 10 # yが目的変数 # 71番目以降に10だけキャンペーン効果が上乗せされている data <- cbind(y, x1) pre.period <- c(1, 70) # キャンペーン前 post.period <- c(71, 100) # キャンペーン後 impact <- CausalImpact(data, pre.period, post.period) # モデル計算を行い、オブジェクトに結果を収納する summary(impact) plot(impact)
Posterior inference {CausalImpact} Average Cumulative Actual 117 3511 Prediction (s.d.) 106 (0.43) 3195 (12.94) 95% CI [106, 107] [3169, 3219] Absolute effect (s.d.) 11 (0.43) 317 (12.94) 95% CI [9.7, 11] [292.4, 343] Relative effect (s.d.) 9.9% (0.41%) 9.9% (0.41%) 95% CI [9.2%, 11%] [9.2%, 11%] Posterior tail-area probability p: 0.00111 Posterior prob. of a causal effect: 99.88901% For more details, type: summary(impact, "report")

{CausalImpact}は、このcounterfactual modelingのバックエンドに{bsts}で推定した状態空間モデルを用いるというところが特徴的です。その{bsts}については理論面にもある程度踏み込んだ詳細なブログ記事があるので、そちらを是非ご覧ください。
僕がブログ記事で書いたものよりも遥かに懇切丁寧に解説されていてお薦めです。また、状態空間モデルについて詳しくないという方向けには良書も沢山ありますが、面倒だという方は以前解説した記事をお読みいただいても良いかと思います。
状態空間モデルには色々な利点がありますが、一番大きいのは欠損値に強い点でしょうか*1。実際{bsts}は学習データに多少の欠損値があってもかなり正確な推定結果を返します。
どのようにcounterfactual modelingしているのか
では、実際には{CausalImpact}はどのようにそのcounterfactual modelingをやっているのでしょうか。これについては、冒頭で紹介した公式資料の2番目の論文のFig.1とそのキャプションを見るのが手っ取り早そうです。
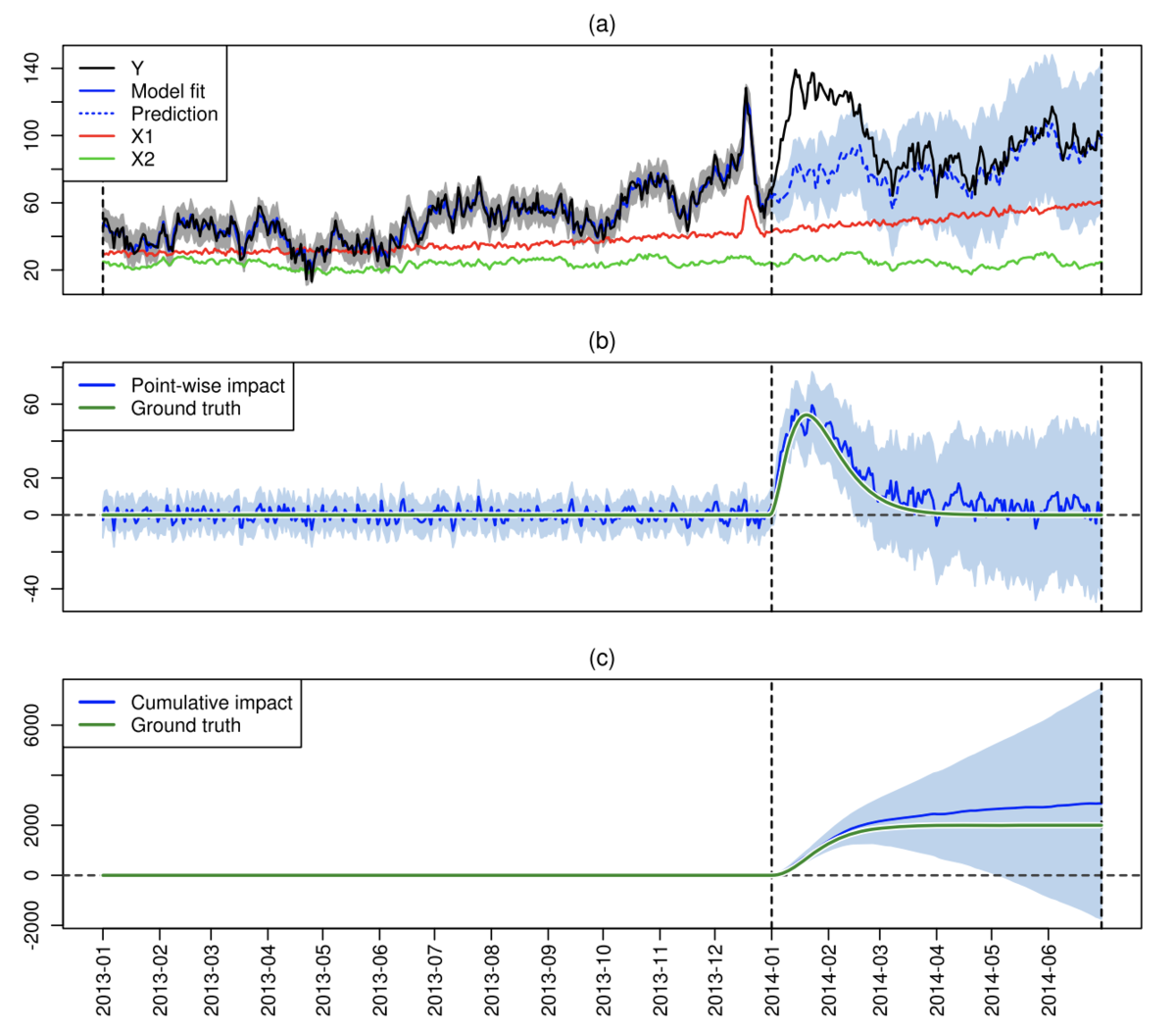

要は「検証したい目的変数の時系列に加えて適切な共変量を用意して、その共変量を用いて目的変数によって{bsts}でモデリングし、介入しなかった場合に得られるであろう目的変数のcounterfactualな時系列と実測値の時系列とを比べて、どれくらい乖離があったかで介入効果の有無や大小を評価する」というものです。
これ自体は上の方で見た説明の繰り返しに過ぎないようにも見えます。ただ、ここで注目すべきは冒頭にリンクしたTogetterまとめでもコメントされていた「共変量の要件」。論文の本文p.252を読むと、
The most important state component for the applications considered in this paper is a regression component that allows us to obtain counterfactual predictions by constructing a synthetic control based on a combination of markets that were not treated. Observed responses from such markets are important because they allow us to explain variance components in the treated market that are not readily captured by more generic seasonal sub-models.
This approach assumes that covariates are unaffected by the effects of treatment. For example, an advertising campaign run in the United States might spill over to Canada or the United Kingdom. When assuming the absence of spill-over effects, the use of such indirectly affected markets as controls would lead to pessimistic inferences, that is, the effect of the campaign would be underestimated [cf. Meyer (1995)].
(太字筆者)
とあり、counterfactual modelingのご利益について述べた上で、共変量は介入による影響を受けないことを想定するものとしています。これ、よくよく考えてみると結構強い仮定なんじゃないでしょうか。
厳密には「差分の差分法」(DiD)を前提としていないが、事実上DiDを要求している
何故上記の要請を「結構強い仮定」と述べたかというと、これは事実上「差分の差分法」(Difference in Differences: DiD)に基づいた測定データであることを要求するものだからです。
つまり、本来的には「あくまでも目的変数(に介入がなかったとした場合の反実仮想)の値を適切にモデリングして予測できる」共変量=説明変数を選べば良いはずなのですが、結局時系列データを扱うことを考えれば「出来る限り介入による影響を受けないものであるべき」という話になるわけです。これが論文p.252で書かれているように「spillover effect*2も排除したものでなければならない」となると、実はmarketing experimentという文脈で見るとRCT(Randomized Controlled Trial: ランダム化比較試験)ほどではないにせよかなり条件統制のされた厳格な実験をやる必要性が出てくることになります。
という強い仮定の上に、さらに例えば「説明変数である以上はランク落ちや多重共線性は避けなければならない」などなどの一般的な時系列モデリング上の注意点も付け加えていくとなると、意外と共変量の選び方は難しいのかもしれません。つまり「介入による効果は受けない」と同時に「spillover effectが互いに生じない」さらには「共変量同士でも何がしかの影響を互いに与えない」ことが期待されるわけで、これを厳密に満たす共変量なんて特にマーケティングの現場だとなかなか見つけにくいのではないでしょうか。
そうすると、あくまでも例えばの話ですが、「出来るだけ潜在的なspillover effectを避けるためにあえて(見かけ上は)無関係そうに見える非介入時系列をある程度多めに揃えることでcounterfactual modelingの予測精度を上げる」みたいな戦略もあり得るのかもしれません。実は、僕自身{CausalImpact}を使い始めた時は共変量の時系列を2つも3つも使う理由がピンと来てなかったんですが、それなら納得がいくという感もあります。
ところが、冒頭でリンクを張った{bsts}の解説ブログ記事にもあったように、そもそもここでのcounterfactual modelの回帰係数の推定にはspike-and-slab事前分布を用いた一種のスパース推定*3が用いられるので、要らない共変量は削られてしまう運命にあるわけです。その辺の試行錯誤を行うために、{CausalImpact}が{bsts}の延長として回帰係数を含んだオブジェクトを返すのを利用して、vignetteにもあるように
plot(impact$model$bsts.model, "coefficients")
などのやり方で「結局どの共変量が残ったか」を確認し、その都度削られた共変量は排除して改めて別の共変量を持ってくる、というような作業が必要になるのかもしれません。
そういう問題意識を持ちながら、DiD + {CausalImpact}という統計的因果推論に基づく介入効果測定のフレームワークを運用していく必要があるのかな?と思い、簡単にまとめてみた次第です。
余談:共変量がなかったらどうなるのか
Vignetteにある例を、そのまま改変してみました。
library(CausalImpact) set.seed(1) x1 <- 100 + arima.sim(model = list(ar = 0.999), n = 52) y <- 1.2 * x1 + rnorm(52) y[41:52] <- y[41:52] + 10 data <- cbind(y, x1) pre.period <- c(1, 40) post.period <- c(41, 52) # 共変量がある場合 impact1 <- CausalImpact(data, pre.period, post.period) plot(impact1) # 共変量がない場合 impact2 <- CausalImpact(as.data.frame(y), pre.period, post.period) plot(impact2)


共変量がある場合は介入効果のposterior interval*4は狭くなり、ない場合はかなり広くなるように見えます。これはソースコードを見れば分かります。
# No regression? if (ncol(data) == 1) { bsts.model <- bsts(y, state.specification = ss, niter = model.args$niter, seed = 1, ping = 0, model.options = BstsOptions(save.prediction.errors = TRUE), max.flips = model.args$max.flips) } else { formula <- paste0(names(data)[1], " ~ .") # Static regression? if (!model.args$dynamic.regression) { bsts.model <- bsts(formula, data = data, state.specification = ss, expected.model.size = kStaticRegressionExpectedModelSize, expected.r2 = kStaticRegressionExpectedR2, prior.df = kStaticRegressionPriorDf, niter = model.args$niter, seed = 1, ping = 0, model.options = BstsOptions(save.prediction.errors = TRUE), max.flips = model.args$max.flips) time(bsts.model$original.series) <- time(data) # Dynamic regression? } else { # Since we have predictor variables in the model, we need to explicitly # make their coefficients time-varying using AddDynamicRegression(). In # bsts(), we are therefore not giving a formula but just the response # variable. We are then using SdPrior to only specify the prior on the # residual standard deviation. # prior.mean: precision of random walk of coefficients sigma.mean.prior <- GammaPrior(prior.mean = 1, a = 4) ss <- AddDynamicRegression(ss, formula, data = data, sigma.mean.prior = sigma.mean.prior) sd.prior <- SdPrior(sigma.guess = model.args$prior.level.sd * sdy, upper.limit = 0.1 * sdy, sample.size = kDynamicRegressionPriorSampleSize) bsts.model <- bsts(y, state.specification = ss, niter = model.args$niter, expected.model.size = 3, ping = 0, seed = 1, prior = sd.prior, max.flips = model.args$max.flips) }
もう見たまんまで、共変量がある場合は当然{bsts}は共変量を外生変数とする回帰モデルを計算しにいくわけですが、ない場合はただの自己回帰モデルを計算するので、単純にモデルの精度*5に差が出るということなんですね。その意味でも「良い共変量を探す」ことは重要なようです。