ちょっと前に、しょうもないことを某所で放言したら思いの外拡散されてしまいました。
機械学習の説明可能性(解釈性)、大半のケースで求められているのは厳密な分類・回帰根拠ではなく受け手の「納得感」なので、特に実ビジネス上は説明可能性に長けたモデルを開発するより、納得できないお客さんを巧みに関係性構築した上で口八丁で完璧に説得できる凄腕営業ピープルを雇う方が重要
— TJO (@TJO_datasci) 2019年11月23日
これ自体は与太話なので実際どうでも良い*1のですが、最近色々な研究や技術開発の進展はたまた実務家による考察などを見ていて、「機械学習の説明可能性(解釈性)というのは思った以上に複雑な迷宮だ」と感じることがままあったのでした。
ということで、今回の記事では僕のサーベイの範囲でザッと見て目についた資料などを超絶大雑把にリストアップした上で、主に実務における説明可能性とは何かという話題について個人的に考えていることを書き出してみたいと思います。なお、このまとめはあくまでも「ビジネス実務における機械学習の説明可能性(解釈性)」という話題を念頭に置いたものであり、学術的な議論や況してや学術発表における引用に耐えるような代物ではありませんので、伏してご了承くださいm(_ _)m
機械学習の説明可能性(解釈性)に関する研究の概要
まず、個々の手法の概要については阪大の原先生のサイトに大変素晴らしいまとめが載っていて、正直言ってこちらをただひたすら上から下まで読んで回るだけで大抵の知識は得られるのではないかと思います。
そして、その原先生ご自身の手によるまとめスライドが非常に端的で分かりやすいので、恐縮ながら以下にある程度引用しながらまとめさせていただきます。なお、こちらのスライドの冒頭では諸手法が以下のように大きく分けられています。
これを踏まえた上で、個々の手法について簡単に概要を見ていきましょう。
局所的な説明
以下、原先生のスライドに載っている著名な手法のみピックアップして紹介しておきます。2019年末現在では当然ながらこれ以外の手法も発表されている旨予めお断りしておきます。
LIME


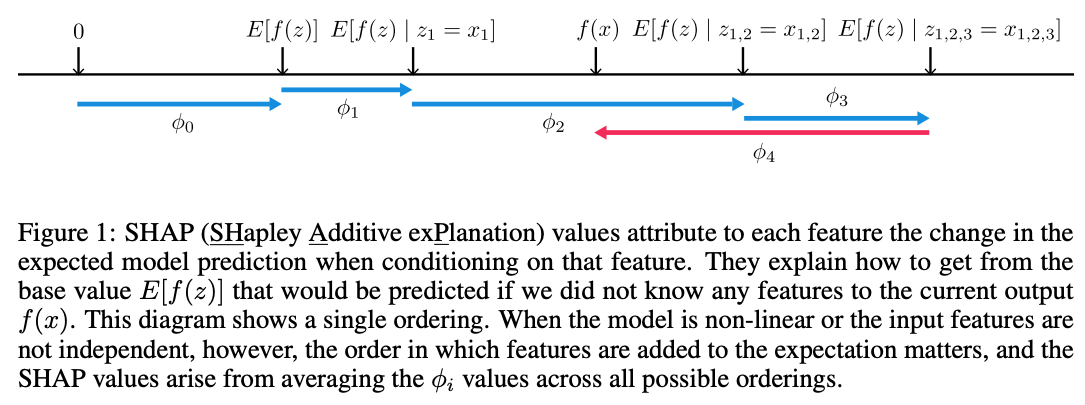
元論文はこちら。どの特徴量が予測に重要だったかを提示するもので、具体的にはモデルを説明対象データの周辺で線形モデルで近似するという方法論。その線形モデルの係数の大小を、各特徴量の重要度とするものです。上のキャプションにもあるように「局所的には合っている(が大局的には合わない)」というやり方です。
Anchor


元論文はこちら。特徴量がどの範囲にあれば(分布していれば)予測に十分かを提示するというもので、なくても精度が変わらない特徴量は任意の値に置き換えても構わないという考え方が根底にあるようです(Figure 3は面白い例かと)。
influence
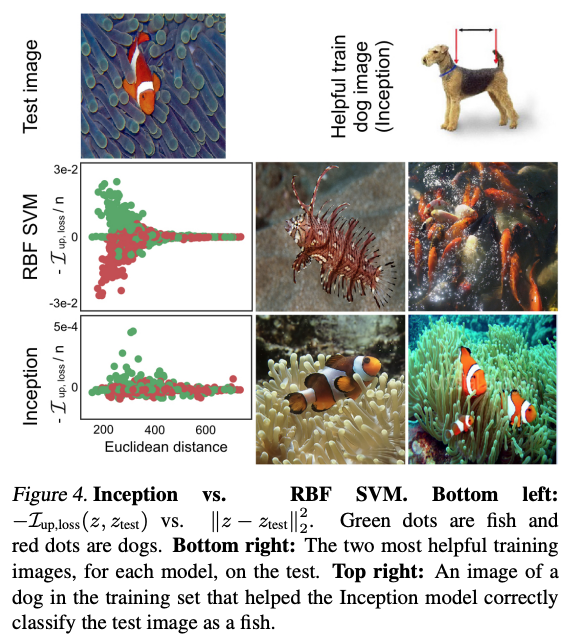

元論文はこちら。「ある特定の学習データ(サンプル)が欠けていたとしたらテストデータの予測結果がどれくらい変わるか」に着目した手法で、これを影響関数の考え方を用いて評価することから"influence"と称するようです。この性質を悪用して、指定したテストデータへの影響の強い学習データに狙ってノイズを乗せて作った「敵対的」学習データを作ることによって、その指定したテストデータへの予測を間違えるようにモデルに対して攻撃を加えることができるという話が載っています(Data Poisoning)。
勾配ベースのハイライト(主にNN系画像認識モデル)

原先生のスライドではオリジナル含めて6つの手法が挙げられていますが、コンセプトとしては互いに似ていて基本的には「認識(分類)に寄与している要素をわずかに変化させた場合に出力が大きく変化する(勾配が大きい)時はそこの注目度が大きいとみなす」というものです。その勾配にノイズが大きいことから、ノイズを減らす手法が複数提案されているということのようです。
大局的な説明
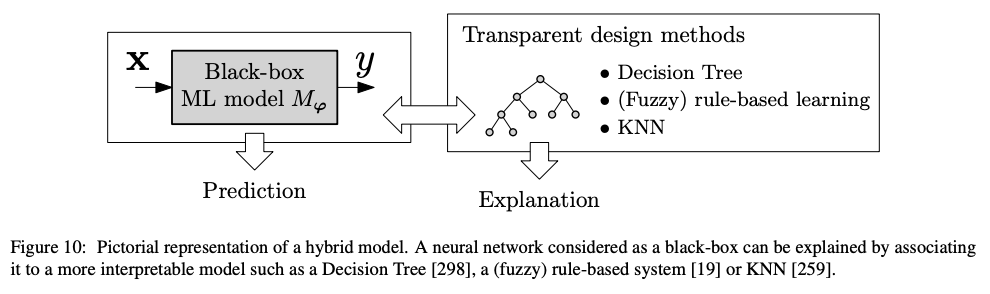
こちらは原先生のスライドではなく別の論文(後述)の図ですが、分かりやすいので引用してみました。即ち、ブラックボックスのNN系モデルを決定木やルールベースモデルはたまたkNNのような、より「ヒトが見て解釈しやすいモデル」に当てはめることで解釈性を高めるという考え方です。

ここでは代表例としてkNNを用いた手法、"DkNN"について引用されている論文を紹介しておきます。NNをまず学習させた上で、個々のレイヤーの説明性をnearest neighborsで与えるというものです。なお、この手法はadversarial exampleに強いという議論があるようですが、この記事では割愛します。
全体のコンセプト
ところで直前にリンクを貼った総説論文は非常に網羅的で、全体の「コンセプト」について細かく説明がなされています。以下のFigure 12が中でもパッと見で最も分かりやすいまとめだと思いました。
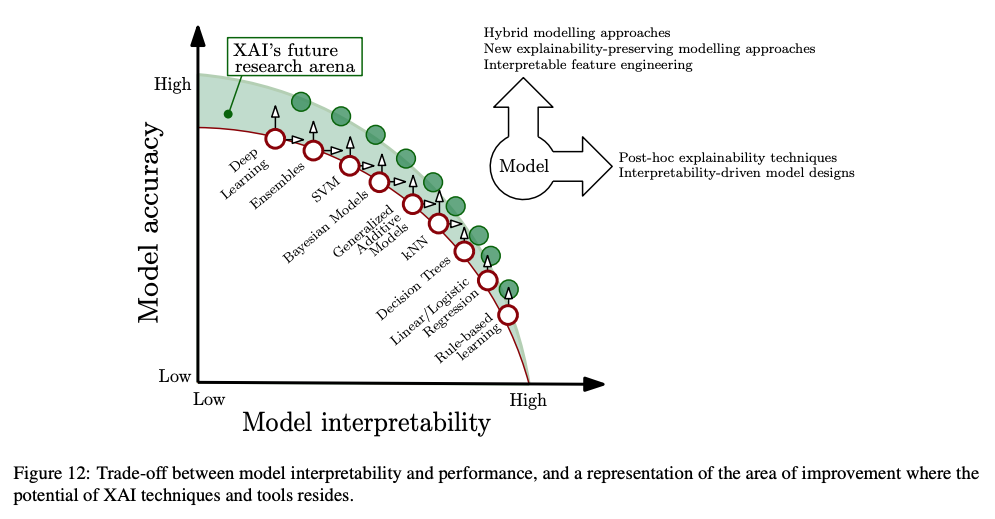
モデルの精度としては「ルールベース<線形モデル<決定木<……<SVM<アンサンブル<Deep Learning」だと言っていますが、モデルの解釈性としてはその真逆で「ルールベース>線形モデル>決定木>……>SVM>アンサンブル>Deep Learning」だと言っているわけです。これはbias-variance tradeoffに次ぐもう一つのtradeoffとして掲げても良いのではないかと思うくらいです(笑)。
勿論、本文中でも非常に網羅的かつ深く踏み込んだ「説明可能性」「解釈性」に関する議論が展開されていて、例えばそもそもinterpretabilityとは何か?とかinterpretabilityはどのような類似概念と関連するか?といった多くのテーマが扱われていますが、それら全てを論っているだけでブログ記事が3本ぐらい書けてしまいそうなのでここでは割愛します。。。
本当にそれは「説明可能」なのか
一方で以下のような批判もあり、個人的には極めて納得のいく議論だと思います。
ブラックボックスの機械学習モデルを解釈する方法を編み出すのをやめなさい、という批判論文。解釈手法は元のモデルを完全に説明できない(もしできたら解釈可能な手法と互換になる)だけでなく、「説明」は多くの場合説明になってないなど様々な点が指摘されている。https://t.co/QZ4iBrwxJb
— piqcy (@icoxfog417) 2019年12月13日
上記の「局所的な説明」にせよ「大局的な説明」にせよ、基本的には「ヒトが直感でも解釈できそうなところを一部取ってくる」もしくは「ヒトが直感でも解釈できそうな別のモデルに何とかして当てはめる」ということをしているに過ぎず、悪い言い方をすると「優れたブラックボックスのMLモデルに対して見かけだけは分かりやすい劣化コピーの代用品を持ってきているだけ」だからです。
また、個人的に交流のある今泉先生の「非滑らかさ」に関する議論も、この文脈における「説明可能にするのは困難」という論旨を補強するものだと自分の中では理解しています。僕の乏しい頭を絞って得られた理解では、結局Deep諸系統のモデルは「ヒトが直感的には理解できないような構造の学習データに対しても多層モデルによって柔軟に対応して優れた当てはまりを実現できる」ということなので、そもそもの原理的な出発点として「ヒトの理解を超えたところで威力を発揮する」ものなのでしょう。裏を返せば、例えば線形分離可能パターンには線形モデルを使おうがDeepを使おうが性能にほとんど差は出ないわけです。
となると、線形分離可能パターンのデータに対してはそもそも線形モデルのようなヒトが理解しやすいモデルがあるから「説明可能性」は問題にならないし、一方で線形分離不可能(極度に)パターンのデータに対してはヒトが理解しやすいモデルは存在し得ないので同様に「説明可能性」を論じるだけ無駄である、ということになります。厳しいツッコミですが、これには首肯せざるを得ないという気もします。
実務の現場にとっての「説明可能性」とは
ところで、ビジネス実務の現場ではどうかという話ですが。冒頭に引用した暴言放言の通りという部分もないわけではなくて、畢竟「使う側が納得できれば良い」というのが実態でしょう。その意味では時々話題になりますが説明可能性や解釈性ではなく、いわば「納得性」だという意見もあったりします。
僕個人の理解では、上記の総説論文も指摘している通りでヒトが理解できるのはいわゆる「弾力性」*2とか「ルールベース」が関の山であり、これを機械学習モデルに置き換えると所詮は(一般化)線形モデルもしくは決定木(回帰木)止まりになる、ということなのでしょう。言い方を変えると、どのみちヒトが現代の機械学習モデルが何をしているかを直感的に理解することはもはや不可能なことであり、どだい不可能なことを何とかしようとするのは多かれ少なかれ不毛な努力だ、とも極論できそうです。
という、ある意味原理的な「不毛性」を踏まえた上でいかにして機械学習モデルの「説明可能性(解釈性)」をどうビジネス実務の現場で担保していくか、というのは悩ましい問題だなぁ、と。。。ビジネスの実務においては機械学習モデルを使う側が「誰」かによる部分も大きいですが、例えば僕が主戦場とする広告・マーケティング分野だと「ある程度統計学の初歩ぐらいなら知っている*3」という広告マンやマーケッターの人たちになるのではないかと思われます。そうなるとやはり線形モデルか決定木が限界いっぱいで、それ以外の説明可能性や解釈性の付与は逆に混乱を招くだけになるかもしれません。
けれども、上記の総説論文のFigure 12が示すように「モデルの精度」と「モデルの説明可能性」とはトレードオフの関係にあるわけです。故に、これは最終的には「使う側がどちらを優先するか」でそのバランスポイントを決めるしかない話でもあります。今後ML/AIが社会に普及していく中で、この問題についてももっと広く知られて然るべきなのかな、と思った次第です。。。
追記 (2020 Feb 02)
原先生の新たなスライドが公開されていました。もう少し最近の話題も追加されていて必読です。