For non-native Japanese speakers: English version is below.
ちょっと前から色々なところでちらほら名前を聞くなぁと思っていたMXnet。どうやらKagglerの間では急速に人気が高まっているようで、最近になってだいぶバグフィックスが進んだらしいというので僕もインストールしてみることにしました。
もうこれはご覧の通りで、あのXgboostも配布しているDMLCが出したものです。既にソースもドキュメントもかなり整備が進んでいて、ImageNetの学習済みモデルも配布されているようです。ということで、早速ちょっと触ってみようと思います。
Convolutional Neural Network (CNN)とは
言うまでもないことだとは思いますが、Convolutional Neural Network (CNN)という手法自体はDeep Learningの発展形として既にそれなりの歴史を持っており、特に画像認識に対して非常に優れた性能を発揮することで以前から良く知られています。つい最近だとAlphaGoの盤面判定に用いられたことでも改めてクローズアップされた手法です。
CNNのライブラリ実装という点についても、古典的なTheanoによるゴリゴリ実装、PyLearn2によるもうちょっと利便性の高い実装*1、Torch / Caffeの隆盛、Chainerの登場による直感的な実装の流行*2、そしてTensorFlow / CNTKといった大手グローバルIT企業による標準化を目指した実装、というように巷に流布するライブラリだけ見てもかなりの変遷があり、最近だとKerasというTheano / TensorFlowのラッパーがあるようでid:aidiaryさんの解説記事が出てます。
ということで、ここではCNN初心者の僕が知ったかぶりをしてCNNについて偉そうなことを書くのは避けます(苦笑)。アルゴリズムの理論的基礎とその実装をざっと学びたいという方は、「畳み込みニューラルネットワーク」とか「Convolutional Neural Network」とかでググれば幾らでも解説資料やブログ記事がヒットするのでそれらをご覧になるか、もしくは例えばこちらの書籍を当たられるのがよろしいかと。
コンセプトだけならこちらの6章を読めば分かるはずです。とりあえず「入力層→『畳み込み層×m→プーリング層(→局所コントラスト層)』×n→全結合層×p→出力層」という構成になっているということだけ覚えておきましょう。
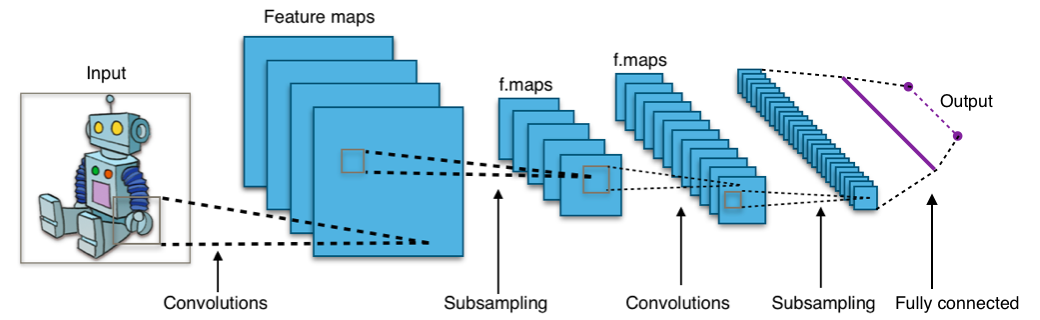
(wikipedia:en:Convolutional_neural_network)
要はやっていることは「ヒトの視覚野で行なわれている情報処理に良く似た処理」です。入力データに対して方位選択性などに基づくフィルタリング処理をした後*3、その平行移動不変性を保つようにして処理し、最後は情報を統合する、というのが大まかな流れかと。なお数学が大の苦手な僕*4がここでその数理的背景を述べるのは不適切なので割愛します(汗)。
MXnetのRパッケージ{mxnet}で手持ちのMNISTショートバージョンの分類タスクを試してみる
ということで、Xgboostも輩出したDMLCが満を持して(?)リリースしたのがそのDeep Learning実装であるMXnetということのようです。ドキュメンテーションに色々書いてあるので詳細はそちらをお読みいただきたいのですが、基本的にはTensorFlow同様にグラフ計算の形でDeep Netを構築・計算するタイプのライブラリです。
最後発の比較的最近のDeep Learning実装ということである意味パイオニアたちのいいとこ取りをやっていて、例えば分散計算もできるし、CPU / GPUの演算切り替えが簡単にできるし、ImageNet学習済みモデルも提供してるし、DNN・CNNに加えてLSTM-RNNも入っているし、対応言語もPython, R, C++, Juliaとデータ分析and/or機械学習界隈が好んで使う言語にターゲットを絞ってカバーしているという優等生っぷり*5。これは使い勝手がいいだろうな〜とドキュメンテーションだけ見て思うレベルです(笑)。
([twitter:@chezou]さんから「MXNetは最後発とありますが、TFより早くリリースされて分散処理もできるフレームワークです。ついに、陽の目を見ることになったのかなぁ - chezou のブックマーク / はてなブックマーク」というブコメをいただきましたので修正しました)
特にRではこれまで良いCNN実装パッケージが皆無と言って良いほどなかったので、MXnetの登場はRユーザーにとっては願ってもない福音だと言っても良いと個人的には思っています。なお個人的なことを書くと、Theanoはコーディングが苦手でPythonで延々組むのがだるくて手を出さず、PyLearn2もそれほど易しくなさそうだったので見送り、Caffe / ChainerはGPUインスタンスを用意するのが面倒でやらず、TensorFlowだけようやく自腹EC2インスタンスにちょろっと入れてCPU版で動かしただけ、みたいな感じだったので、CPU / GPU問わずRで動いてくれるMXnetは本当に有難い限りです。
そんなわけで実際にRパッケージである{mxnet}を使ってMXnetがどう動くかをチュートリアルに沿って試してみましょう。一応、実行環境を以下に書いておきます。
- マシン:MacBook Pro / OS X El Capitan 10.11.3
- プロセッサ:3.1 GHz Intel Core i7
- メモリ:16 GB
- R環境:R 3.2.3 / RStudio 0.99.491
お気付きの方もいるかと思いますが、今年からMacユーザーも兼ねるようになりました(笑)。そしてさらに完全に余談ですが、このスペックのMacBook Proだと大体のローカルでやる系の機械学習計算は余裕ですね。もう自腹EC2インスタンスに頼らなくてもいいかも。
インストール
非常に簡単で、以下のようにやれば入ります。
# Installation > install.packages("drat", repos="https://cran.rstudio.com") > drat:::addRepo("dmlc") > install.packages("mxnet") > library(mxnet)
devtoolsではなくdratで入れるというところが何となく2016年っぽいですね(何がやねん)。
データセットの準備
セクションのタイトルにも書いたように、僕のGitHubリポジトリに置いてあるMNISTのショートバージョン(学習データ5000行&テストデータ1000行)を使います。このデータセットは比較的小さいので、分類器の学習をかなり頑張ってもそれほど精度が上がりません(おそらく98%を超えるのは無理なのでは)。以下のようにして{mxnet}で読み込める形式にまで変換しておきます。
# Data preparation > train<-read.csv('https://github.com/ozt-ca/tjo.hatenablog.samples/raw/master/r_samples/public_lib/jp/mnist_reproduced/short_prac_train.csv') > test<-read.csv('https://github.com/ozt-ca/tjo.hatenablog.samples/raw/master/r_samples/public_lib/jp/mnist_reproduced/short_prac_test.csv') > train<-data.matrix(train) > test<-data.matrix(test) > train.x<-train[,-1] > train.y<-train[,1] > train.x<-t(train.x/255) > test_org<-test > test<-test[,-1] > test<-t(test/255) > table(train.y) train.y 0 1 2 3 4 5 6 7 8 9 500 500 500 500 500 500 500 500 500 500
何度か利用しているデータセットなのでご存知かもですが、一応分類クラスは均衡させてあります。
Deep Neural Network (DNN)で試してみる
では、まずはチュートリアルに従って古典的なDNNで試してみましょう。特に捻りも何にもない、誤差逆伝播つき多層パーセプトロンです。
# Deep NN > data <- mx.symbol.Variable("data") > fc1 <- mx.symbol.FullyConnected(data, name="fc1", num_hidden=128) > act1 <- mx.symbol.Activation(fc1, name="relu1", act_type="relu") > fc2 <- mx.symbol.FullyConnected(act1, name="fc2", num_hidden=64) > act2 <- mx.symbol.Activation(fc2, name="relu2", act_type="relu") > fc3 <- mx.symbol.FullyConnected(act2, name="fc3", num_hidden=10) > softmax <- mx.symbol.SoftmaxOutput(fc3, name="sm") > devices <- mx.cpu() > mx.set.seed(0) > model <- mx.model.FeedForward.create(softmax, X=train.x, y=train.y, + ctx=devices, num.round=10, array.batch.size=100, + learning.rate=0.07, momentum=0.9, eval.metric=mx.metric.accuracy, + initializer=mx.init.uniform(0.07), + epoch.end.callback=mx.callback.log.train.metric(100)) Start training with 1 devices [1] Train-accuracy=0.470204081632653 [2] Train-accuracy=0.8326 [3] Train-accuracy=0.9052 [4] Train-accuracy=0.9278 [5] Train-accuracy=0.9466 [6] Train-accuracy=0.9568 [7] Train-accuracy=0.9646 [8] Train-accuracy=0.9756 [9] Train-accuracy=0.9888 [10] Train-accuracy=0.9926 > preds <- predict(model, test, ctx=devices) > dim(preds) [1] 10 1000 > pred.label <- max.col(t(preds)) - 1 > table(pred.label) pred.label 0 1 2 3 4 5 6 7 8 9 95 101 101 94 104 104 99 107 102 93 > head(pred.label) [1] 0 0 0 6 0 0 > table(test_org[,1],pred.label) pred.label 0 1 2 3 4 5 6 7 8 9 0 94 0 1 0 0 0 3 0 1 1 1 0 100 0 0 0 0 0 0 0 0 2 0 0 97 1 1 0 0 1 0 0 3 0 0 2 91 0 3 0 1 2 1 4 0 0 0 0 95 0 2 1 0 2 5 0 1 0 1 0 96 0 0 2 0 6 1 0 0 0 1 3 94 0 1 0 7 0 0 0 0 0 0 0 100 0 0 8 0 0 1 1 1 1 0 0 96 0 9 0 0 0 0 6 1 0 4 0 89 > sum(diag(table(test_org[,1],pred.label)))/1000 [1] 0.952
ということで、0.952という正答率が得られました。後述しますが、これはまぁ良くも悪くもないという程度のスコアです。
Convolutional Neural Network (CNN)で試してみる
ではでは、いよいよ本題のCNNを試してみましょう。チュートリアルのコードに従えば、おそらく下図のようなCNNの構成になるはずです。

以下のRコードを見れば分かりますが、割とTorchとかChainerっぽくかなり直感的に畳み込み層・プーリング層のそれぞれを記述できることが分かるかと思います。
# Convolutional NN > data <- mx.symbol.Variable('data') > # first conv > conv1 <- mx.symbol.Convolution(data=data, kernel=c(5,5), num_filter=20) > tanh1 <- mx.symbol.Activation(data=conv1, act_type="tanh") > pool1 <- mx.symbol.Pooling(data=tanh1, pool_type="max", + kernel=c(2,2), stride=c(2,2)) > # second conv > conv2 <- mx.symbol.Convolution(data=pool1, kernel=c(5,5), num_filter=50) > tanh2 <- mx.symbol.Activation(data=conv2, act_type="tanh") > pool2 <- mx.symbol.Pooling(data=tanh2, pool_type="max", + kernel=c(2,2), stride=c(2,2)) > # first fullc > flatten <- mx.symbol.Flatten(data=pool2) > fc1 <- mx.symbol.FullyConnected(data=flatten, num_hidden=500) > tanh3 <- mx.symbol.Activation(data=fc1, act_type="tanh") > # second fullc > fc2 <- mx.symbol.FullyConnected(data=tanh3, num_hidden=10) > # loss > lenet <- mx.symbol.SoftmaxOutput(data=fc2) > train.array <- train.x > dim(train.array) <- c(28, 28, 1, ncol(train.x)) > test.array <- test > dim(test.array) <- c(28, 28, 1, ncol(test)) > mx.set.seed(0) > devices <- mx.cpu() > tic <- proc.time() > model <- mx.model.FeedForward.create(lenet, X=train.array, y=train.y, + ctx=devices, num.round=20, array.batch.size=100, + learning.rate=0.05, momentum=0.9, wd=0.00001, + eval.metric=mx.metric.accuracy, + epoch.end.callback=mx.callback.log.train.metric(100)) Start training with 1 devices [1] Train-accuracy=0.0959183673469388 [2] Train-accuracy=0.0902 [3] Train-accuracy=0.0982 [4] Train-accuracy=0.2254 [5] Train-accuracy=0.7958 [6] Train-accuracy=0.9074 [7] Train-accuracy=0.942 [8] Train-accuracy=0.9626 [9] Train-accuracy=0.9762 [10] Train-accuracy=0.9814 [11] Train-accuracy=0.9846 [12] Train-accuracy=0.988 [13] Train-accuracy=0.993 [14] Train-accuracy=0.996 [15] Train-accuracy=0.9988 [16] Train-accuracy=0.9996 [17] Train-accuracy=0.9996 [18] Train-accuracy=1 [19] Train-accuracy=1 [20] Train-accuracy=1 > print(proc.time() - tic) ユーザ システム 経過 270.122 1.216 234.877 > preds <- predict(model, test.array, ctx=devices) > pred.label <- max.col(t(preds)) - 1 > table(test_org[,1],pred.label) pred.label 0 1 2 3 4 5 6 7 8 9 0 97 0 0 0 0 0 3 0 0 0 1 0 100 0 0 0 0 0 0 0 0 2 0 0 99 0 0 0 0 1 0 0 3 0 0 1 96 0 0 0 0 2 1 4 0 0 0 0 97 0 1 1 0 1 5 0 0 0 0 0 98 1 0 1 0 6 1 0 0 0 0 1 98 0 0 0 7 0 1 1 0 1 0 0 96 0 1 8 0 0 1 0 0 0 0 0 99 0 9 0 0 0 0 2 1 0 0 1 96 > sum(diag(table(test_org[,1],pred.label)))/1000 [1] 0.976
正答率0.976というスコアを叩き出してくれました。なおチュートリアルではnum.round = 1のままになっていますが*6、僕が自分で試行錯誤した結果20まで増やしてあります。計算時間も270秒と、同様の計算を例えば{h2o}でやった時に比べてもずっと速いです。これは凄い。
ちなみに試しに「本来なら9のはず」なのにこのCNNによって4, 5, 8に誤判定されたテストデータ4つを取り出してプロットしたものがこちら。

こんなの分かんねーよ!と言いたくなるようなものは、さすがに{mxnet}のチュートリアル通りのCNN程度ではさすがに分類できないようです。まぁ、こういうのをそれでも頑張って分類してのけるのがMNISTの醍醐味なんでしょうけど(笑)。
他手法との比較
僕の手持ちのMNISTショートバージョンで0.976っていうのは、実は過去にブログで試してきた各種分類器によるベンチマークの中ではベストスコアだったりします。以下3つだけ直近のブログ記事でも試した他のベンチマークを挙げておきます。
ランダムフォレスト
> train<-read.csv('https://github.com/ozt-ca/tjo.hatenablog.samples/raw/master/r_samples/public_lib/jp/mnist_reproduced/short_prac_train.csv') > test<-read.csv('https://github.com/ozt-ca/tjo.hatenablog.samples/raw/master/r_samples/public_lib/jp/mnist_reproduced/short_prac_test.csv') > train$label<-as.factor(train$label) > test$label<-as.factor(test$label) > library(randomForest) > train.rf<-randomForest(label~.,train) > table(test$label,predict(train.rf,newdata=test[,-1])) 0 1 2 3 4 5 6 7 8 9 0 96 0 0 0 0 0 3 0 1 0 1 0 99 0 0 0 0 0 0 1 0 2 0 0 96 1 1 0 1 1 0 0 3 0 0 2 87 0 4 1 1 3 2 4 0 0 0 0 96 0 1 0 0 3 5 1 2 0 1 0 94 2 0 0 0 6 0 0 1 0 1 2 95 0 1 0 7 0 2 0 0 1 0 0 93 0 4 8 0 0 1 0 0 0 0 0 99 0 9 0 0 0 0 2 1 0 1 0 96 > sum(diag(table(test$label,predict(train.rf,newdata=test[,-1]))))/nrow(test) [1] 0.951
0.951でした。まぁこれでもtuneRFを省略(計算負荷の問題で)した結果なので、チューニングさえ良ければもっと良くなる気もしますが。
Xgboost
> train<-read.csv('https://github.com/ozt-ca/tjo.hatenablog.samples/raw/master/r_samples/public_lib/jp/mnist_reproduced/short_prac_train.csv') > test<-read.csv('https://github.com/ozt-ca/tjo.hatenablog.samples/raw/master/r_samples/public_lib/jp/mnist_reproduced/short_prac_test.csv') > library(xgboost) > library(Matrix) # データの前処理に必要 > train.mx<-sparse.model.matrix(label~., train) > test.mx<-sparse.model.matrix(label~., test) # データセットをxgboostで扱える形式に直す > dtrain<-xgb.DMatrix(train.mx, label=train$label) > dtest<-xgb.DMatrix(test.mx, label=test$label) # 色々パラメータがあるがxgboostのGitHubなどを参照のこと > train.gbdt<-xgb.train(params=list(objective="multi:softmax", num_class=10, eval_metric="mlogloss", eta=0.3, max_depth=5, subsample=1, colsample_bytree=0.5), data=dtrain, nrounds=70, watchlist=list(train=dtrain,test=dtest)) [0] train-mlogloss:1.439942 test-mlogloss:1.488160 [1] train-mlogloss:1.083675 test-mlogloss:1.177975 [2] train-mlogloss:0.854107 test-mlogloss:0.977648 # ... omitted ... [67] train-mlogloss:0.004172 test-mlogloss:0.176068 [68] train-mlogloss:0.004088 test-mlogloss:0.176044 [69] train-mlogloss:0.004010 test-mlogloss:0.176004 > table(test$label,predict(train.gbdt,newdata=dtest)) 0 1 2 3 4 5 6 7 8 9 0 95 0 0 1 0 0 3 0 1 0 1 0 99 0 0 0 0 0 1 0 0 2 0 0 96 2 0 0 1 1 0 0 3 0 0 1 93 0 0 0 1 2 3 4 0 0 1 1 95 0 1 0 0 2 5 0 1 0 1 0 98 0 0 0 0 6 0 0 1 0 1 2 95 0 1 0 7 0 0 0 0 1 0 0 96 0 3 8 0 4 1 0 1 0 0 0 93 1 9 0 0 0 0 4 1 0 2 0 93 > sum(diag(table(test$label,predict(train.gbdt,newdata=dtest))))/nrow(test) [1] 0.953
0.953でした。これは色々手動でパラメータチューニングしてみた結果得られた(暫定ながら)最高値なので、まぁこんなもんかなぁと。
DNN by {h2o}
> train<-read.csv('https://github.com/ozt-ca/tjo.hatenablog.samples/raw/master/r_samples/public_lib/jp/mnist_reproduced/short_prac_train.csv') > test<-read.csv('https://github.com/ozt-ca/tjo.hatenablog.samples/raw/master/r_samples/public_lib/jp/mnist_reproduced/short_prac_test.csv') > train$label<-as.factor(train$label) > test$label<-as.factor(test$label) > library(h2o) # Java VMのインスタンスを立てる > localH2O <- h2o.init(ip = "localhost", port = 54321, startH2O = TRUE, nthreads=3) # 現行バージョンではas.h2o関数でRオブジェクトを直接読み込める > trData<-as.h2o(train) > tsData<-as.h2o(test) # 以下最適化周りのパラメータ指定が山ほど並んでいるので、Deep Learningの専門書などを参照のこと > res.dl <- h2o.deeplearning(x = 2:785, y = 1, training_frame = trData, activation = "RectifierWithDropout",hidden=c(1024,1024,2048),epochs = 300, adaptive_rate = FALSE, rate=0.01, rate_annealing = 1.0e-6,rate_decay = 1.0, momentum_start = 0.5,momentum_ramp = 5000*18, momentum_stable = 0.99, input_dropout_ratio = 0.2,l1 = 1.0e-5,l2 = 0.0,max_w2 = 15.0, initial_weight_distribution = "Normal",initial_weight_scale = 0.01,nesterov_accelerated_gradient = T, loss = "CrossEntropy", fast_mode = T, diagnostics = T, ignore_const_cols = T,force_load_balance = T) > pred<-h2o.predict(res.dl,tsData[,-1]) > pred.df<-as.data.frame(pred) > table(test$label,pred.df[,1]) 0 1 2 3 4 5 6 7 8 9 0 96 0 1 0 0 0 2 1 0 0 1 0 100 0 0 0 0 0 0 0 0 2 0 0 97 0 2 0 0 1 0 0 3 0 0 1 93 0 4 0 1 0 1 4 0 2 1 0 93 0 0 1 1 2 5 0 0 0 1 0 99 0 0 0 0 6 1 0 0 0 0 2 97 0 0 0 7 0 0 0 0 1 0 0 96 0 3 8 0 0 1 1 1 2 0 0 95 0 9 0 0 0 0 2 0 0 2 0 96 > sum(diag(table(test$label,pred.df[,1])))/nrow(test) [1] 0.962
H2Oがどこかで提示していたベストチューニングで0.962、これなら{mxnet}のDNNでチュートリアルを完コピして回した結果よりは良いということになります。とは言え、{mxnet}のCNNでチュートリアルを完コピして回した適当な結果の方が0.976で優れているというのはなかなか示唆的で。。。そりゃみんな画像認識課題が来たら当然CNNやりますよね、という。
感想など
一つは、とにかく使いやすいということ。CPU / GPUの切り替えも簡単なので、例えばGPUも用意できる環境なら必要に応じて使い分けられるわけです。二つ目は、計算速度が速いということ。DMLCが以前出したXgboostもそうなんですが、とにかく速い。Java VM分散環境ベースの{h2o}のDNNよりも、{mxnet}だとCNNであってもずっと速いというのは大きなメリットだと思います。
そしてR / Pythonユーザーにしてアドホック分析メインの人間として嬉しいのは、RでもPythonでも同じようにCNNを回せるというところ。これまたDMLCが以前出したXgboostでもそうなんですが、これには実務面で特に大きなメリットがあります。
と言うのも、R上でプロトタイプ開発として「1人Kaggle」みたいな機械学習業務をやっている人って割とデータ分析業界には少なくないと思うんですが、そういうケースでも{mxnet}を使えば「まずR上でプロトタイプを組んで性能を確認してから、Python実装に切り替えてプロダクト環境に回す」みたいな芸当もできるわけですね。もちろん最初からPythonでやればいいんですが(笑)、手元でごちゃごちゃデータを取り回す際にはRの方が便利なことも多いので、プロトタイプ開発はRでやる方が個人的には楽です。実はXgboostでそういう「Rでプロトタイプ開発→Pythonでプロダクト向けコード」という手順を僕もやったことがあるので、その意味ではCNNをビジネス実務で使う上では{mxnet}は非常に便利なライブラリ・パッケージだと言えると思います。
もっともバラ色の話ばかりではもちろんなくて、例えばパラメータチューニングなんかは今でもCNNではつらみネタとして引き合いに出されるようなところでしょう。最近は[twitter:@issei_sato]先生がやられているようなベイジアンの枠組みでCNNのパラメータ最適化を回すみたいな発想もあるようですが、そこまでローカルマシンの{mxnet}でやってたら日が暮れるどころか年が暮れそうです(泣)。この辺はいかな{mxnet}で便利になったとは言っても、いつまでも重い課題として残りそうですね。。。
とは言え、Chainer / TensorFlowでDeep Learning実装ライブラリ競争はほぼケリが付いたと思っていたところにこのMXnetが出てきて、まただいぶ面白くなってきたなあと思っているところです。今後も面白いライブラリ・パッケージが登場することを期待しようと思います。
そうそう、この{mxnet}には他にもLSTM-RNNなんかも実装されているので、系列データでも面白いことが出来るんじゃないかなぁということで気が向いたら何かまた別の記事を書くかもしれません。気が向いたら、ですが(笑)。そんなわけで、いつも通り「炎上ラーニング」期待モードで多くの識者の皆様からのツッコミをお待ちしております。。。
余談
@toshi_k_datasci ひそかにTJO先生より早く何か出せるか検討したいと思います。
— Slowly but surely. (@Keiku) 2016年3月28日
元はと言えば日本が誇るKaggle masterのお一人[twitter:@Keiku]さんが{mxnet}について呟いていらしたのを見かけたのがこの記事の発端なので、きっと[twitter:@Keiku]さんがこんな「手持ちの軽いデータで回しました(鼻ほじ)」みたいな軽い記事よりもずっと重厚な記事を出して下さるのではと期待しております(笑)*7。
追記1
ということで、[twitter:@Keiku]さんが僕の無茶振りにお応え下さり、素晴らしいブログ記事をupして下さいました。僕の「やってみました」系記事より遥かに実践的で、一読の価値大アリです。
http://keiku.hatenablog.jp/entry/2016/03/31/172456
詳細は記事をお読みいただきたいのですが、個人的に大いに参考になったのが現役バリバリのKagglerの間での現状認識に関する下り。以下引用。
また、最近では、Kaggle等のコンペティションにてGBDTのライブラリであるXGBoostが猛威をふるっているとたびたび話題にあがりますが、Kagglerから正確に現状を伝えると、XGBoostとDeep Learningのアンサンブルが猛威をふるっているというのが今の状況です。そしてこのOtto Challengeは、XGBoostだけでなく、Deep Learningの威力をまざまざと見せつけられた代表的な事例であると言えるでしょう。このコンペティションの上位者は絶対と言っていいほど、XGBoostとDeep Learningのアンサンブルを行っています。XGBoostでほとんどの参加者が良い精度を出すのは当たり前となっているため、ゆえにDeep Learningがいかにできるかが勝敗を分ける鍵であったと思います。
Deep Learningライブラリ「MXNet」のR版をKaggle Otto Challengeで実践してみた - Think more, try less
この辺が、流石は純粋に機械学習の精度を競う「競技機械学習」(?)の世界ならではのお話だなぁと思いました。実務の現場だとまだまだXgboost / Deep Learningが別個に投入されているようなケースが多いと思うのですが、コンペの世界では既にこの両者をアンサンブルさせるというレベルにまで来ているという。。。例えば今回の{mxnet}のような実装により高速化がさらに進んだら、バンバンstackingさせて精度を上げに行くような展開が広がっていくのかな?とか、色々期待が膨らみますね。
追記2
Dropoutを入れてみました。
> # first conv > conv1 <- mx.symbol.Convolution(data=data, kernel=c(5,5), num_filter=20) > tanh1 <- mx.symbol.Activation(data=conv1, act_type="tanh") > pool1 <- mx.symbol.Pooling(data=tanh1, pool_type="max", + kernel=c(2,2), stride=c(2,2)) > drop1 <- mx.symbol.Dropout(data=pool1,p=0.5) > # second conv > conv2 <- mx.symbol.Convolution(data=pool1, kernel=c(5,5), num_filter=50) > tanh2 <- mx.symbol.Activation(data=conv2, act_type="tanh") > pool2 <- mx.symbol.Pooling(data=tanh2, pool_type="max", + kernel=c(2,2), stride=c(2,2)) > drop2 <- mx.symbol.Dropout(data=pool2,p=0.5) > # first fullc > flatten <- mx.symbol.Flatten(data=drop2) > fc1 <- mx.symbol.FullyConnected(data=flatten, num_hidden=500) > tanh3 <- mx.symbol.Activation(data=fc1, act_type="tanh") > drop3 <- mx.symbol.Dropout(data=tanh3,p=0.5) > # second fullc > fc2 <- mx.symbol.FullyConnected(data=drop3, num_hidden=10) > # loss > lenet <- mx.symbol.SoftmaxOutput(data=fc2) > train.array <- train.x > dim(train.array) <- c(28, 28, 1, ncol(train.x)) > test.array <- test > dim(test.array) <- c(28, 28, 1, ncol(test)) > mx.set.seed(0) > devices <- mx.cpu() > tic <- proc.time() > model <- mx.model.FeedForward.create(lenet, X=train.array, y=train.y, + ctx=devices, num.round=50, array.batch.size=100, + learning.rate=0.05, momentum=0.9, wd=0.00001, + eval.metric=mx.metric.accuracy, + epoch.end.callback=mx.callback.log.train.metric(100)) Start training with 1 devices Start training with 1 devices [1] Train-accuracy=0.0957142857142857 [2] Train-accuracy=0.0904 [3] Train-accuracy=0.0952 [4] Train-accuracy=0.2304 [5] Train-accuracy=0.7618 [6] Train-accuracy=0.8676 [7] Train-accuracy=0.901 [8] Train-accuracy=0.9224 [9] Train-accuracy=0.9372 [10] Train-accuracy=0.9428 [11] Train-accuracy=0.9484 [12] Train-accuracy=0.956 [13] Train-accuracy=0.9592 [14] Train-accuracy=0.9598 [15] Train-accuracy=0.965 [16] Train-accuracy=0.9664 [17] Train-accuracy=0.966 [18] Train-accuracy=0.9698 [19] Train-accuracy=0.9716 [20] Train-accuracy=0.9732 [21] Train-accuracy=0.9762 [22] Train-accuracy=0.9764 [23] Train-accuracy=0.9792 [24] Train-accuracy=0.9772 [25] Train-accuracy=0.9772 [26] Train-accuracy=0.981799999999999 [27] Train-accuracy=0.9762 [28] Train-accuracy=0.9814 [29] Train-accuracy=0.981 [30] Train-accuracy=0.982 [31] Train-accuracy=0.9874 [32] Train-accuracy=0.9814 [33] Train-accuracy=0.9782 [34] Train-accuracy=0.9848 [35] Train-accuracy=0.9862 [36] Train-accuracy=0.9834 [37] Train-accuracy=0.9834 [38] Train-accuracy=0.989 [39] Train-accuracy=0.9834 [40] Train-accuracy=0.98 [41] Train-accuracy=0.9864 [42] Train-accuracy=0.9858 [43] Train-accuracy=0.9868 [44] Train-accuracy=0.9872 [45] Train-accuracy=0.9878 [46] Train-accuracy=0.989 [47] Train-accuracy=0.989 [48] Train-accuracy=0.9838 [49] Train-accuracy=0.9858 [50] Train-accuracy=0.9878 > print(proc.time() - tic) ユーザ システム 経過 620.661 3.279 543.105 > preds <- predict(model, test.array, ctx=devices) > pred.label <- max.col(t(preds)) - 1 > table(test_org[,1],pred.label) pred.label 0 1 2 3 4 5 6 7 8 9 0 98 0 0 0 0 0 2 0 0 0 1 0 99 0 0 0 0 0 0 1 0 2 0 0 98 1 0 0 0 1 0 0 3 0 0 1 96 0 0 0 0 2 1 4 0 1 0 0 97 0 0 1 0 1 5 0 0 0 0 0 100 0 0 0 0 6 1 0 0 0 0 1 98 0 0 0 7 0 0 0 0 0 0 0 99 1 0 8 0 0 1 0 0 0 0 0 99 0 9 0 0 0 0 2 0 0 0 0 98 > sum(diag(table(test_org[,1],pred.label)))/1000 [1] 0.982
0.982まで上がりました。予想していた上限0.98を超えて何よりです。もちろんDropoutを入れたことで少し学習に時間がかかっていますが、その代わり学習の収束もややばらついているような。。。
(※実は上のモデル記述のところでチェーンを間違えているところがあって、そこを正しく直したら0.985までいきました)
追記3
ReLUに替えてDropoutしてみたら、もっと良くなりました。
> data <- mx.symbol.Variable("data") > devices<-mx.cpu() > # first conv > conv1 <- mx.symbol.Convolution(data=data, kernel=c(5,5), num_filter=20) > tanh1 <- mx.symbol.Activation(data=conv1, act_type="relu") > pool1 <- mx.symbol.Pooling(data=tanh1, pool_type="max", + kernel=c(2,2), stride=c(2,2)) > drop1 <- mx.symbol.Dropout(data=pool1,p=0.5) > # second conv > conv2 <- mx.symbol.Convolution(data=drop1, kernel=c(5,5), num_filter=50) > tanh2 <- mx.symbol.Activation(data=conv2, act_type="relu") > pool2 <- mx.symbol.Pooling(data=tanh2, pool_type="max", + kernel=c(2,2), stride=c(2,2)) > drop2 <- mx.symbol.Dropout(data=pool2,p=0.5) > # first fullc > flatten <- mx.symbol.Flatten(data=drop2) > fc1 <- mx.symbol.FullyConnected(data=flatten, num_hidden=500) > tanh4 <- mx.symbol.Activation(data=fc1, act_type="relu") > drop4 <- mx.symbol.Dropout(data=tanh4,p=0.5) > # second fullc > fc2 <- mx.symbol.FullyConnected(data=drop4, num_hidden=10) > # loss > lenet <- mx.symbol.SoftmaxOutput(data=fc2) > train.array <- train.x > dim(train.array) <- c(28, 28, 1, ncol(train.x)) > test.array <- test > dim(test.array) <- c(28, 28, 1, ncol(test)) > mx.set.seed(0) > devices <- mx.cpu() > tic <- proc.time() > model <- mx.model.FeedForward.create(lenet, X=train.array, y=train.y, + ctx=devices, num.round=60, array.batch.size=100, + learning.rate=0.05, momentum=0.9, wd=0.00001, + eval.metric=mx.metric.accuracy, + epoch.end.callback=mx.callback.log.train.metric(100)) Start training with 1 devices [1] Train-accuracy=0.0975510204081633 [2] Train-accuracy=0.0906 [3] Train-accuracy=0.09 [4] Train-accuracy=0.0952 [5] Train-accuracy=0.1312 [6] Train-accuracy=0.5612 [7] Train-accuracy=0.8384 [8] Train-accuracy=0.8974 [9] Train-accuracy=0.9156 [10] Train-accuracy=0.9296 [11] Train-accuracy=0.9366 [12] Train-accuracy=0.9436 [13] Train-accuracy=0.9452 [14] Train-accuracy=0.943 [15] Train-accuracy=0.9504 [16] Train-accuracy=0.9566 [17] Train-accuracy=0.955 [18] Train-accuracy=0.9634 [19] Train-accuracy=0.9636 [20] Train-accuracy=0.9594 [21] Train-accuracy=0.9624 [22] Train-accuracy=0.9644 [23] Train-accuracy=0.964 [24] Train-accuracy=0.9628 [25] Train-accuracy=0.9658 [26] Train-accuracy=0.9674 [27] Train-accuracy=0.971 [28] Train-accuracy=0.9692 [29] Train-accuracy=0.9716 [30] Train-accuracy=0.9766 [31] Train-accuracy=0.9712 [32] Train-accuracy=0.9758 [33] Train-accuracy=0.9694 [34] Train-accuracy=0.9694 [35] Train-accuracy=0.9688 [36] Train-accuracy=0.9768 [37] Train-accuracy=0.9728 [38] Train-accuracy=0.9744 [39] Train-accuracy=0.971 [40] Train-accuracy=0.9722 [41] Train-accuracy=0.9746 [42] Train-accuracy=0.9758 [43] Train-accuracy=0.9794 [44] Train-accuracy=0.9756 [45] Train-accuracy=0.9746 [46] Train-accuracy=0.9778 [47] Train-accuracy=0.9766 [48] Train-accuracy=0.9768 [49] Train-accuracy=0.976799999999999 [50] Train-accuracy=0.977399999999999 [51] Train-accuracy=0.9786 [52] Train-accuracy=0.978 [53] Train-accuracy=0.9786 [54] Train-accuracy=0.9774 [55] Train-accuracy=0.9808 [56] Train-accuracy=0.976 [57] Train-accuracy=0.9762 [58] Train-accuracy=0.9794 [59] Train-accuracy=0.978 [60] Train-accuracy=0.9822 > print(proc.time() - tic) ユーザ システム 経過 784.666 3.767 677.921 > preds <- predict(model, test.array, ctx=devices) > pred.label <- max.col(t(preds)) - 1 > table(test_org[,1],pred.label) pred.label 0 1 2 3 4 5 6 7 8 9 0 99 0 0 0 0 0 1 0 0 0 1 0 99 0 0 1 0 0 0 0 0 2 0 0 98 0 0 0 0 1 1 0 3 0 0 0 98 0 1 0 0 1 0 4 0 2 0 0 97 0 1 0 0 0 5 0 0 0 0 0 99 1 0 0 0 6 0 0 0 0 0 0 100 0 0 0 7 0 0 0 0 0 0 0 99 1 0 8 0 0 0 0 0 0 0 0 100 0 9 0 0 0 0 2 0 0 0 0 98 > sum(diag(table(test_org[,1],pred.label)))/1000 [1] 0.987
0.987まで到達しました。ってかこれ頑張ってもっとチューニングすれば0.99いけるかも?
